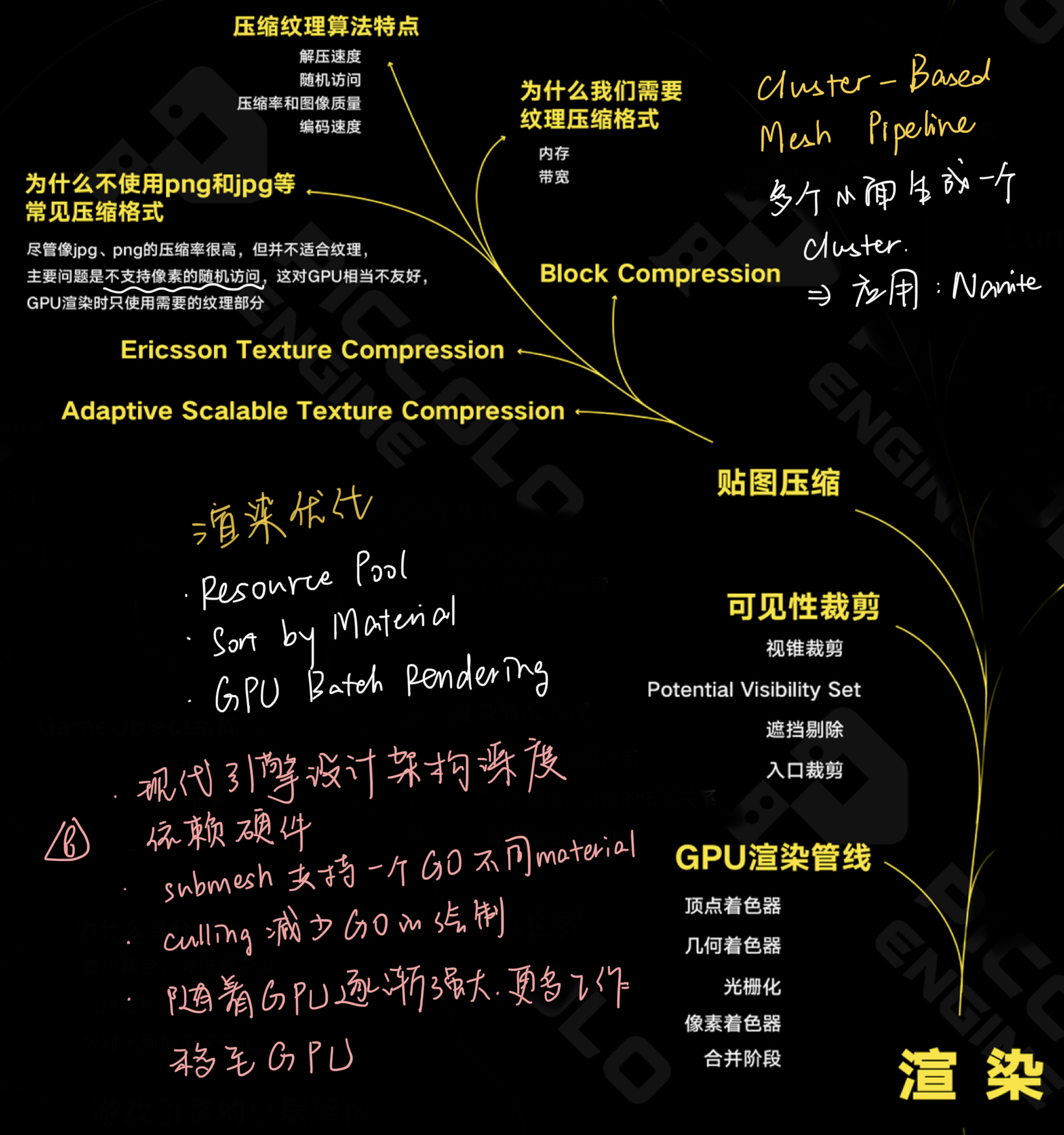
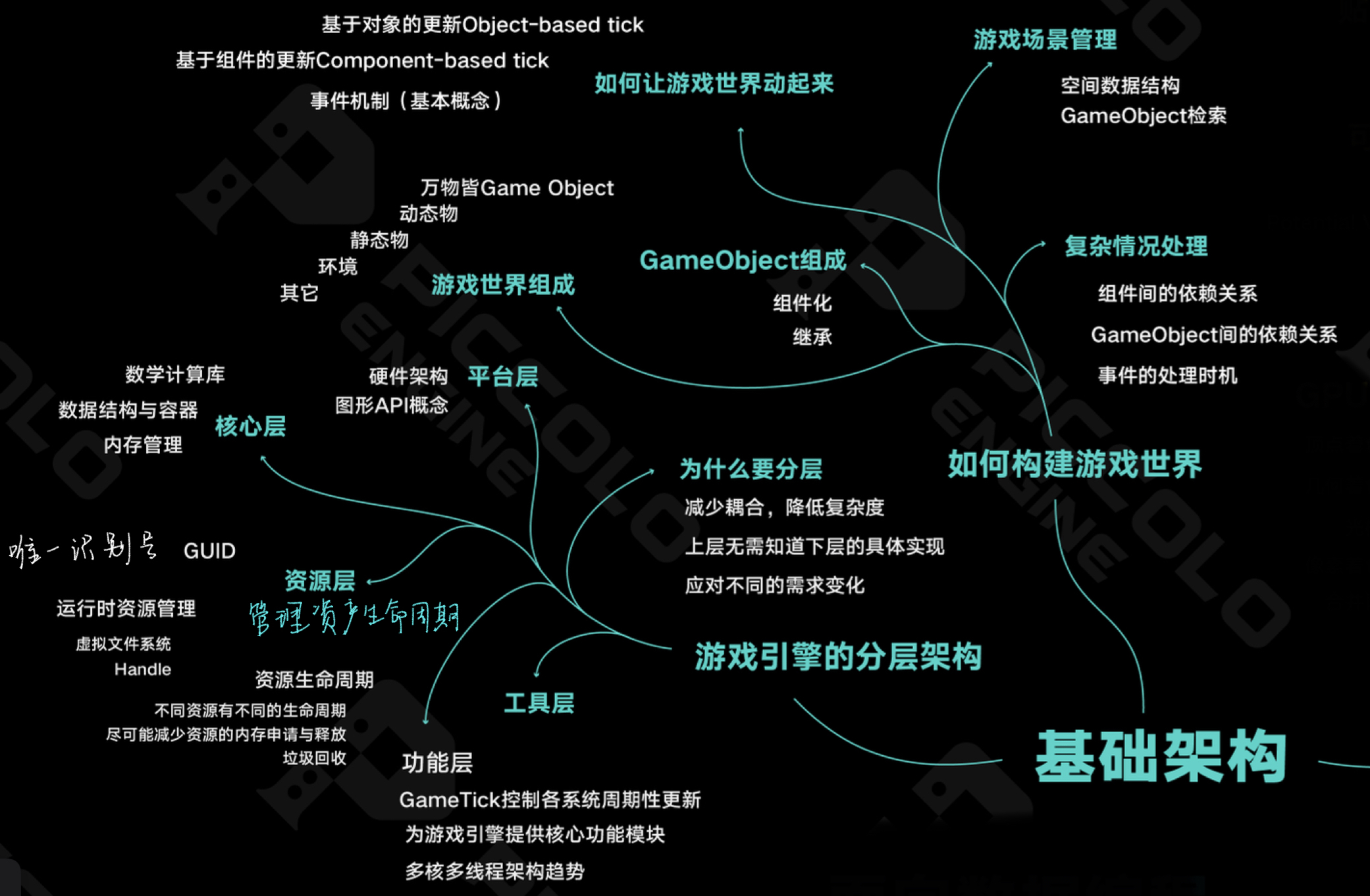
暂别
尘封已久的博客啊,好久不见。翻看着之前的笔记,仿佛在透过屏幕看曾经的自己。
没再更新笔记的这小一年的时间里,我确实经历了很多事情。我在时而焦虑内耗,又时而干劲满满、热烈快活的日子里摸爬滚打。蓦然回首,确实已经走过了很长的一段路;纵然向前,也发现阶段性的目的地已经发生了变化。
打碎,再重塑,如此循环,似乎是对这大半年抽象却最精准的概括。客观的世界是相同的,不同之处在于每个人看待这个世界的方式。人生似乎就像是在训练一个大模型,每一段人生经历都像在对这个模型做微调训练。而最终模型的推理,就是在认知这个世界。
实话讲,去年的我真的很拧巴,归根到底大概是想不明白自己这么做的目的。贸然前行,却发现心不在此。虽然如此,我却真心地感激着过去这一年的经历。这些的经历塑造了现在的我,而我现在的认知也促使我选择了当下的阶段性目的地。
说回写下这段矫情碎碎念的最初目的——这个博客也许会停更很长一段时间。图形学和TA都很有意思,但也许不是当下的我最想去深入了解的了。我在试图探索一些更交叉杂糅的领域,目标和方向改变没关系,坚定就好。
那么,暂别啦。祝所有人生活愉快。