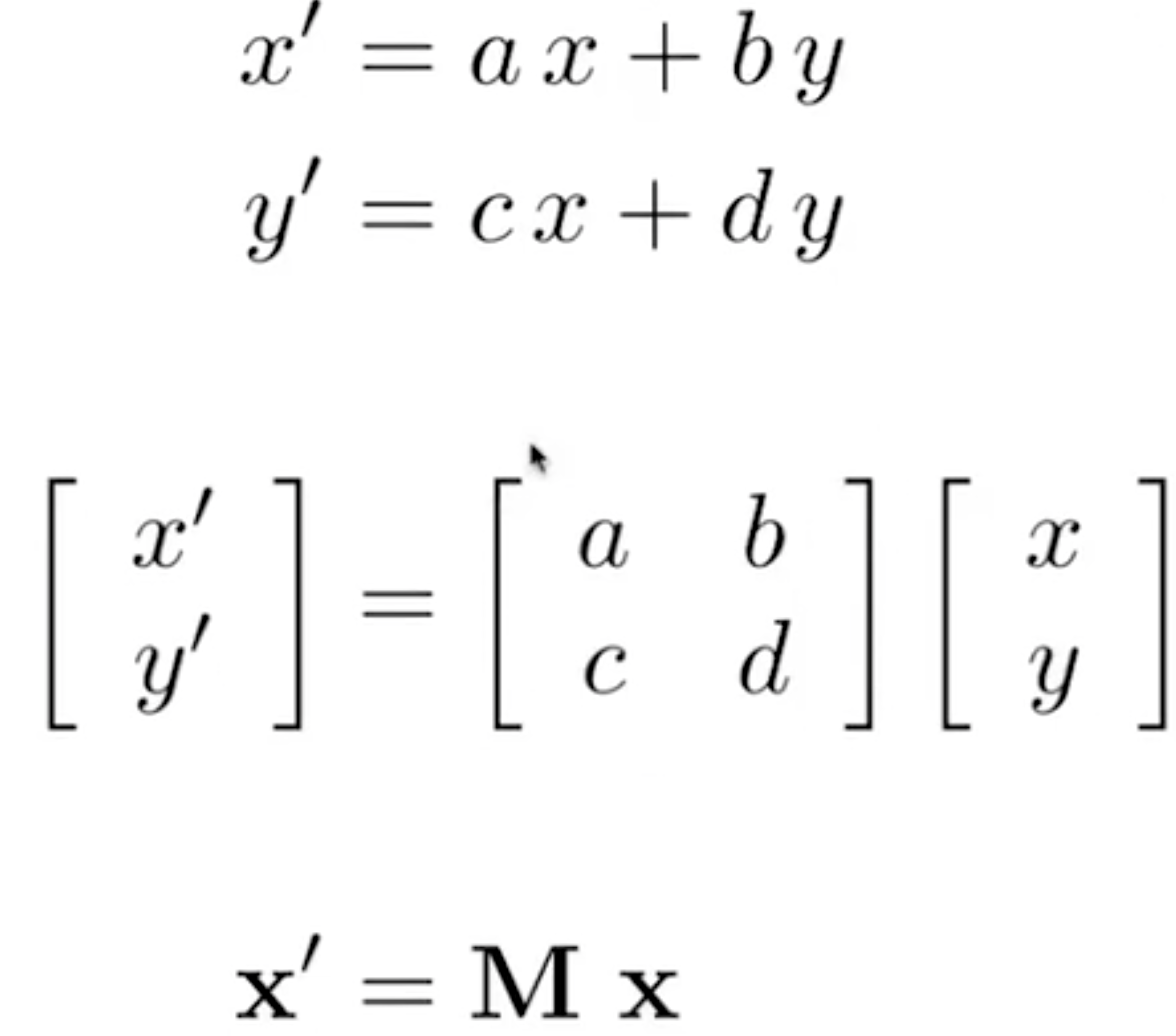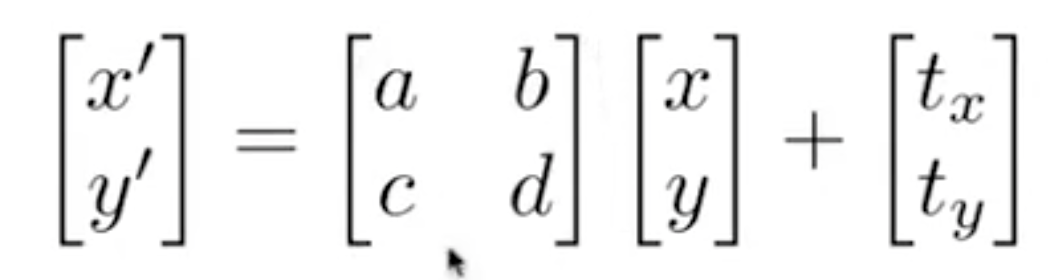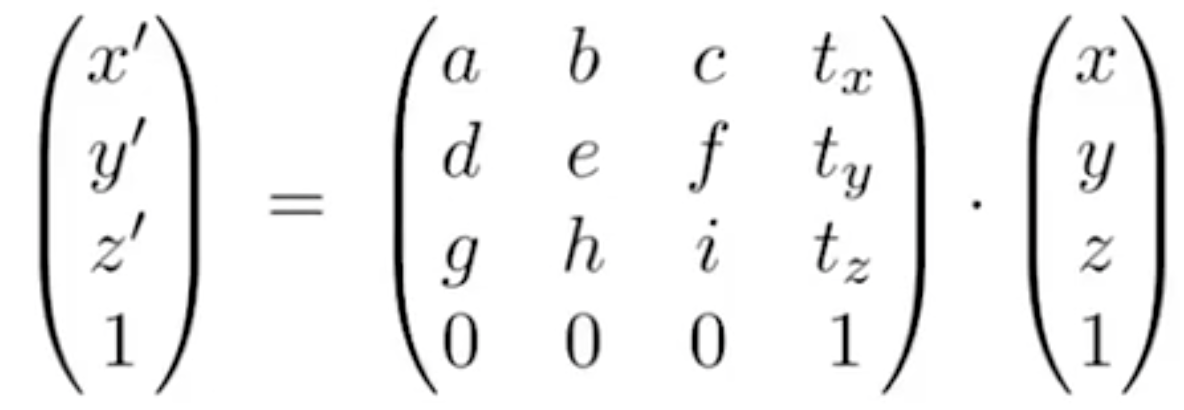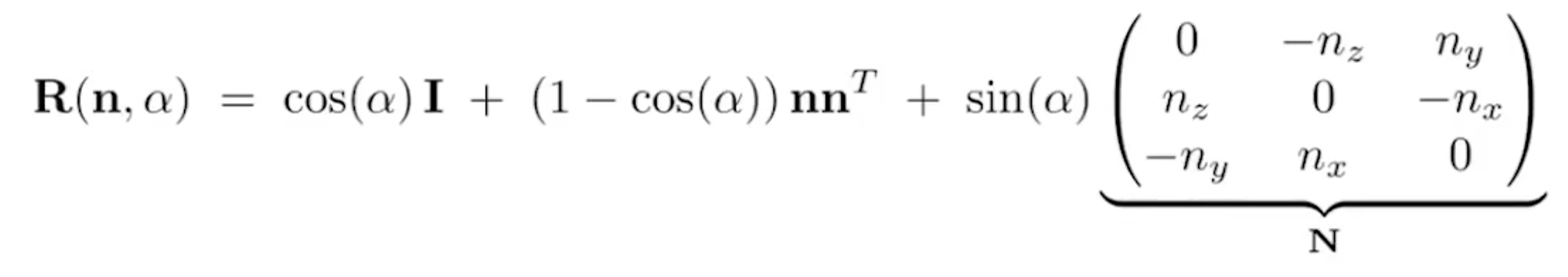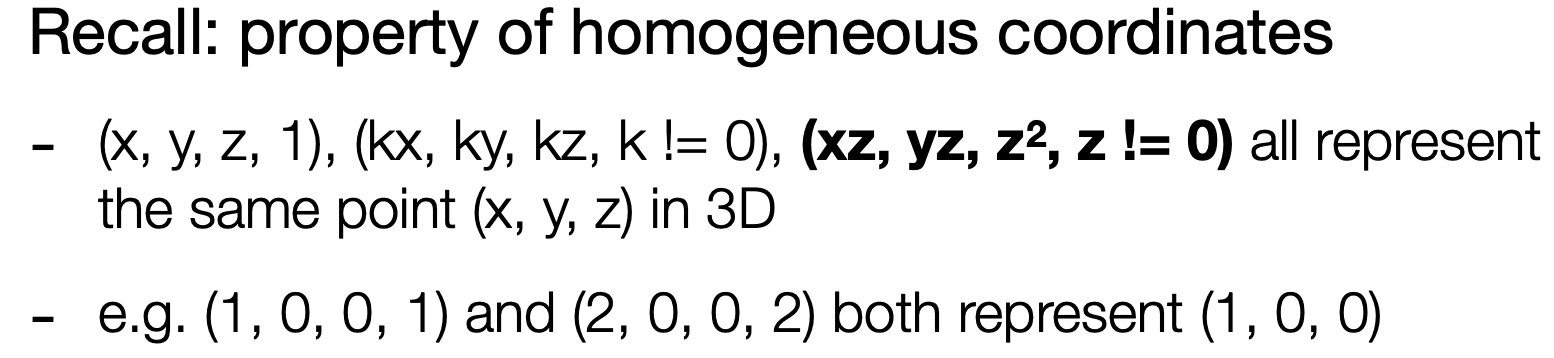Games101-P3-4 Transformation

Posted on Edited on In Word count in article: 1.9k
  • P3 Preview
    • Why study transformation
    • 2D变换：rotation, scale, shear
    • 其次坐标：增加一维表示平移变换
    • 复合变换
  • P4 Preview
    • 3D变换
    • Viewing(观测) Transformation
      • View(视图)/Camera Transformation
      • Projection(投影) Transformation
        • Orthographic(正交)
        • Perspective(透视)

P3-4 Transformation

P3

Transformation

  • Modeling模型变换
  • Viewing视图变换：（3D to 2D）projection

2D Transformation

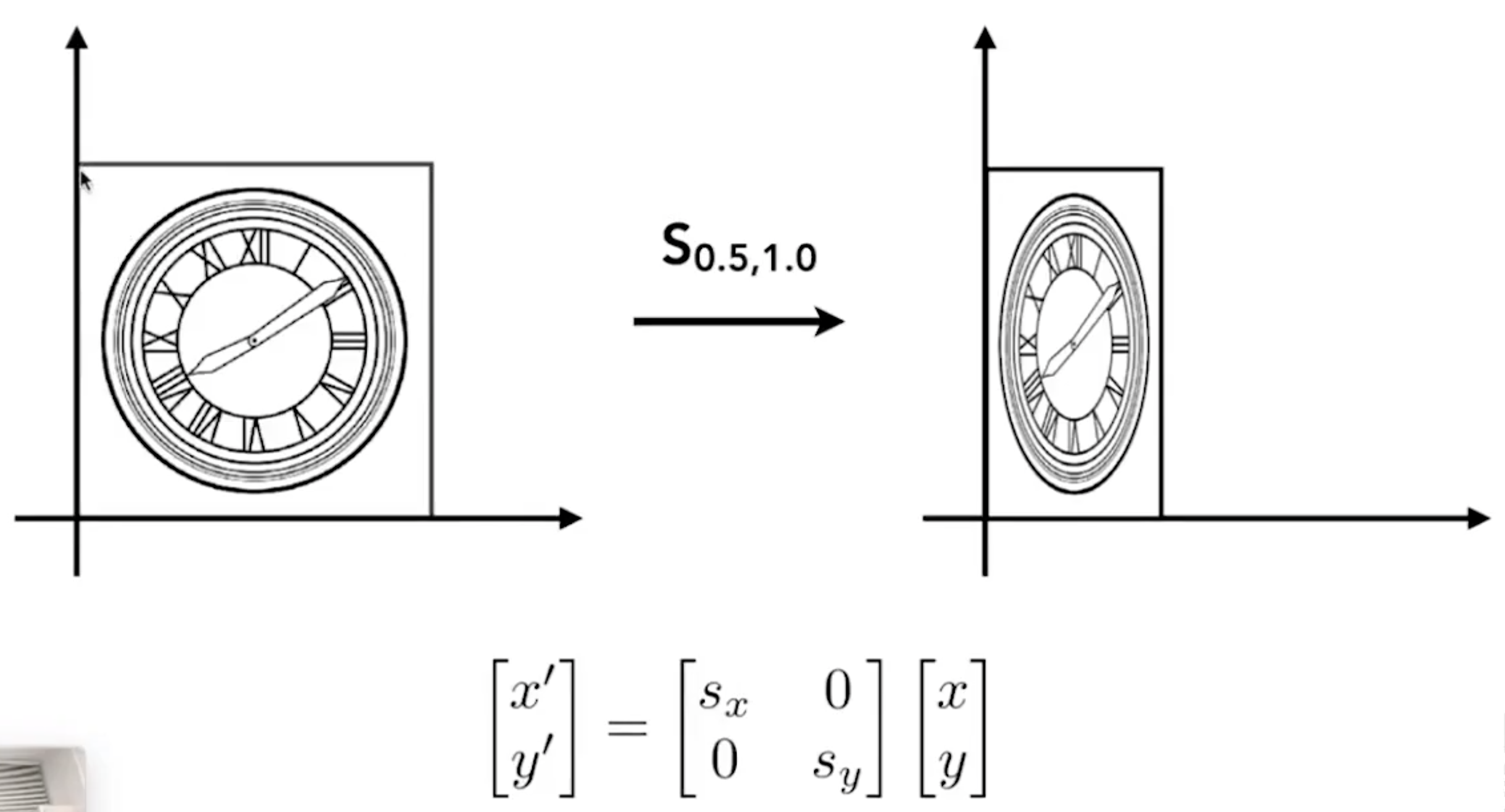
  • Scale
    • 截屏2023-03-21 20.16.25
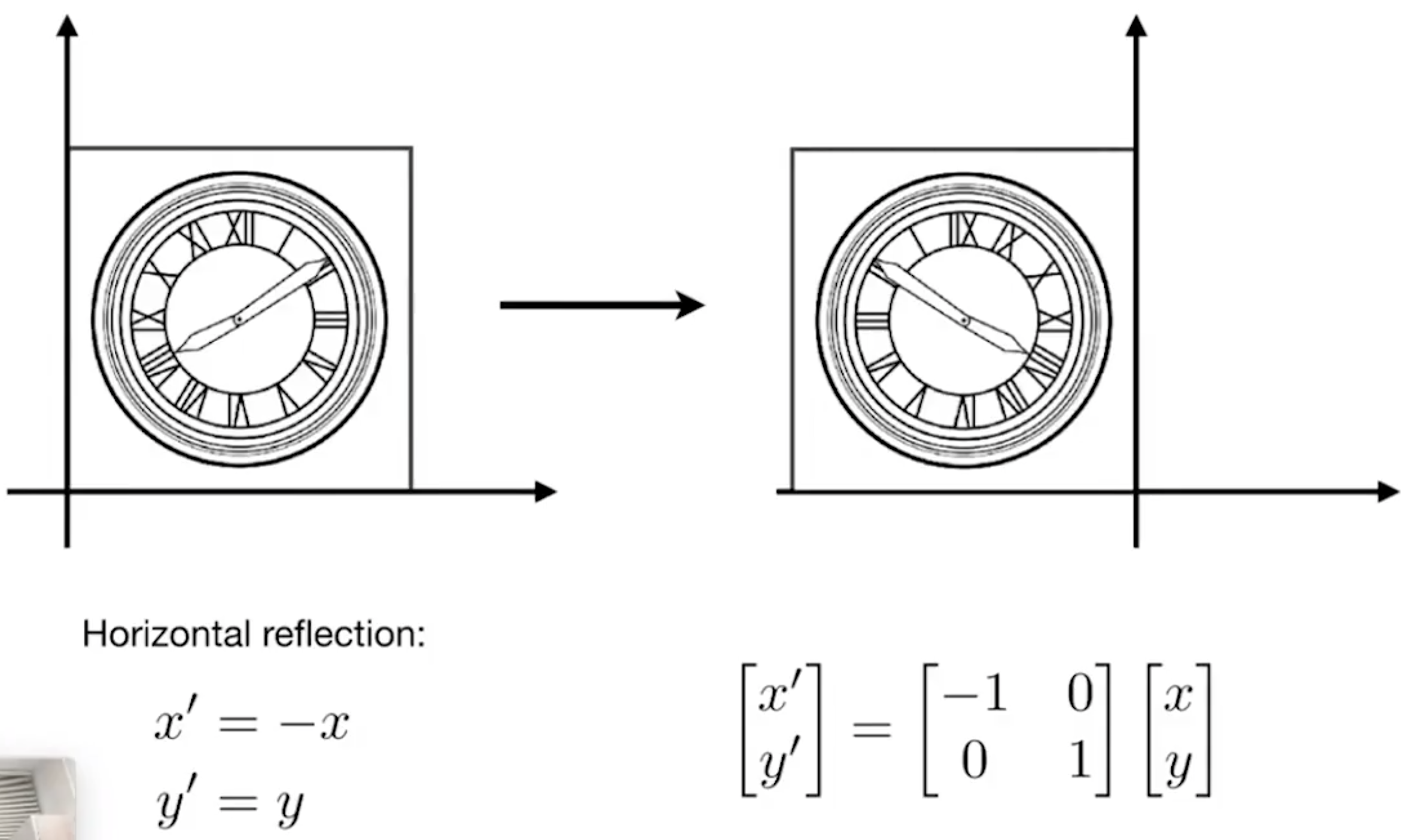
  • Reflection
    • 截屏2023-03-21 20.18.45
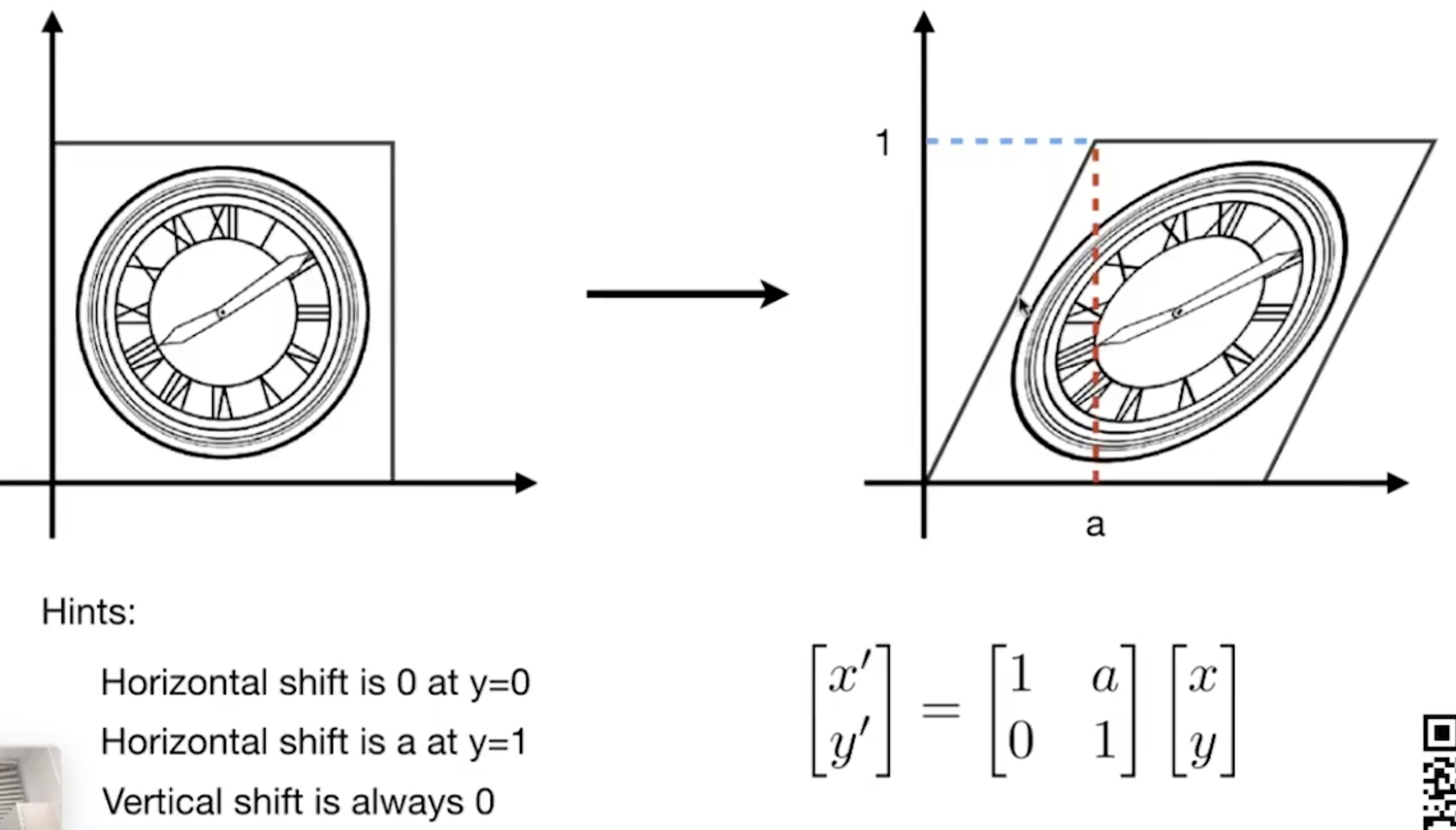
  • Shear(切变)
    • 截屏2023-03-21 20.24.18
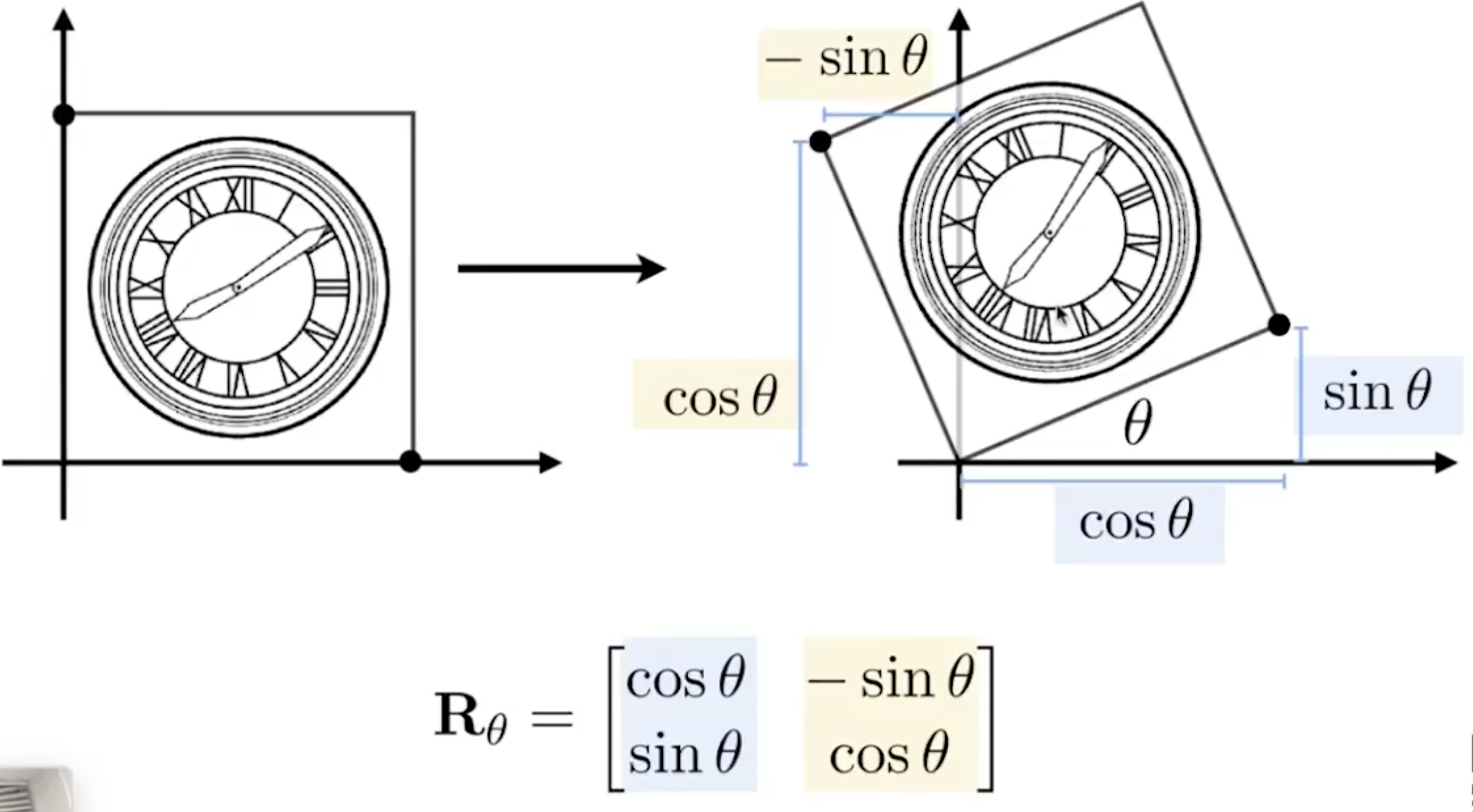
  • Rotation（特殊化点，推导（旋转绕原点
    • 截屏2023-03-21 20.27.31
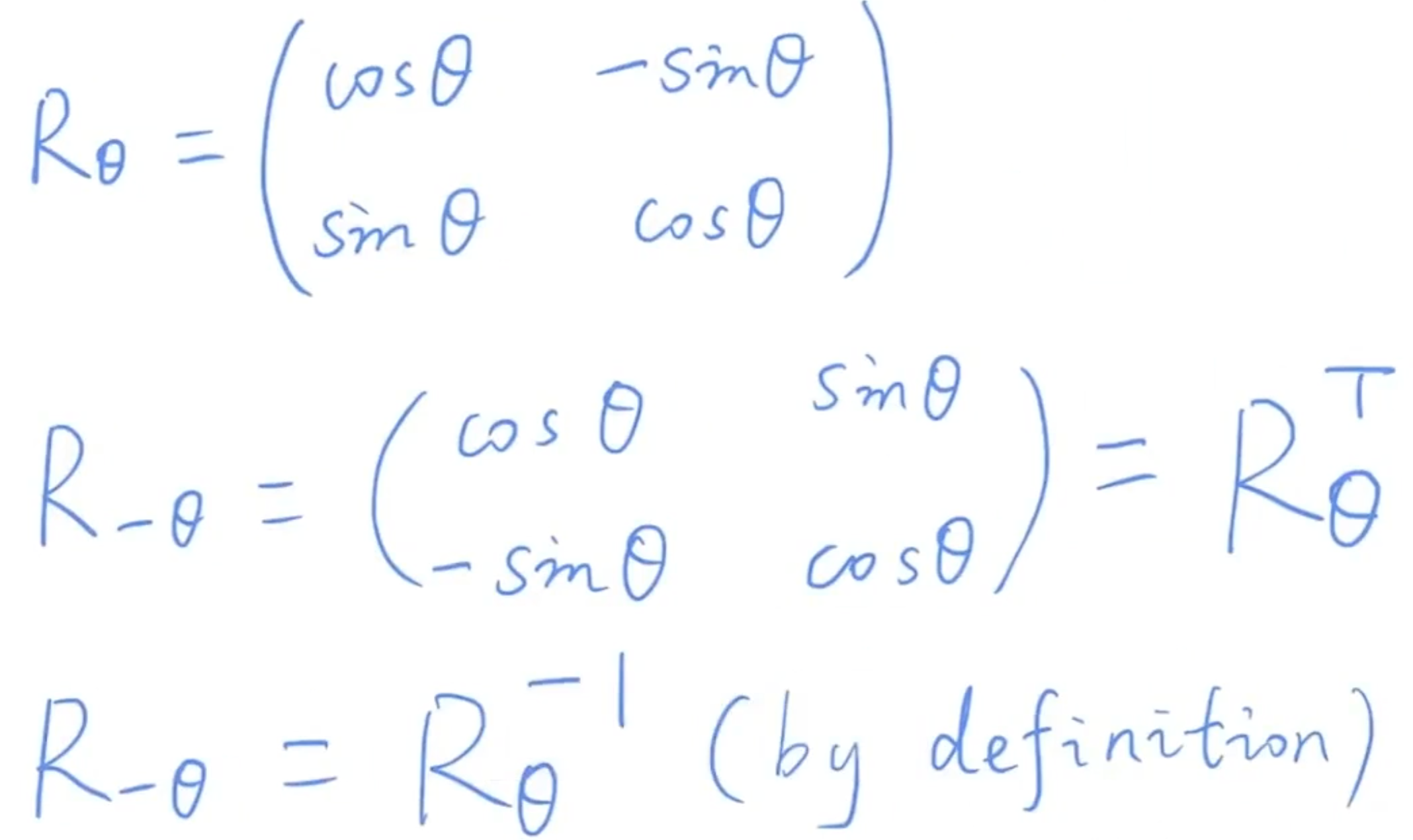
    • 截屏2023-03-27 10.12.13
      • 正交矩阵，转置 = 逆
  • 线性变换（写成矩阵形式
    • 截屏2023-03-21 21.15.53

其次坐标

  • 平移变换——非线性变换，上述矩阵无法满足

    • 截屏2023-03-26 21.13.00

  • 引入其次坐标

    • 截屏2023-03-26 21.18.19
    • 1和0用于区分是点还是向量
      • 向量是0: 因为向量具有平移不变性
    • 截屏2023-03-26 21.27.22
      • point + point得到两点间中点
  • Affine Transform 仿射变换
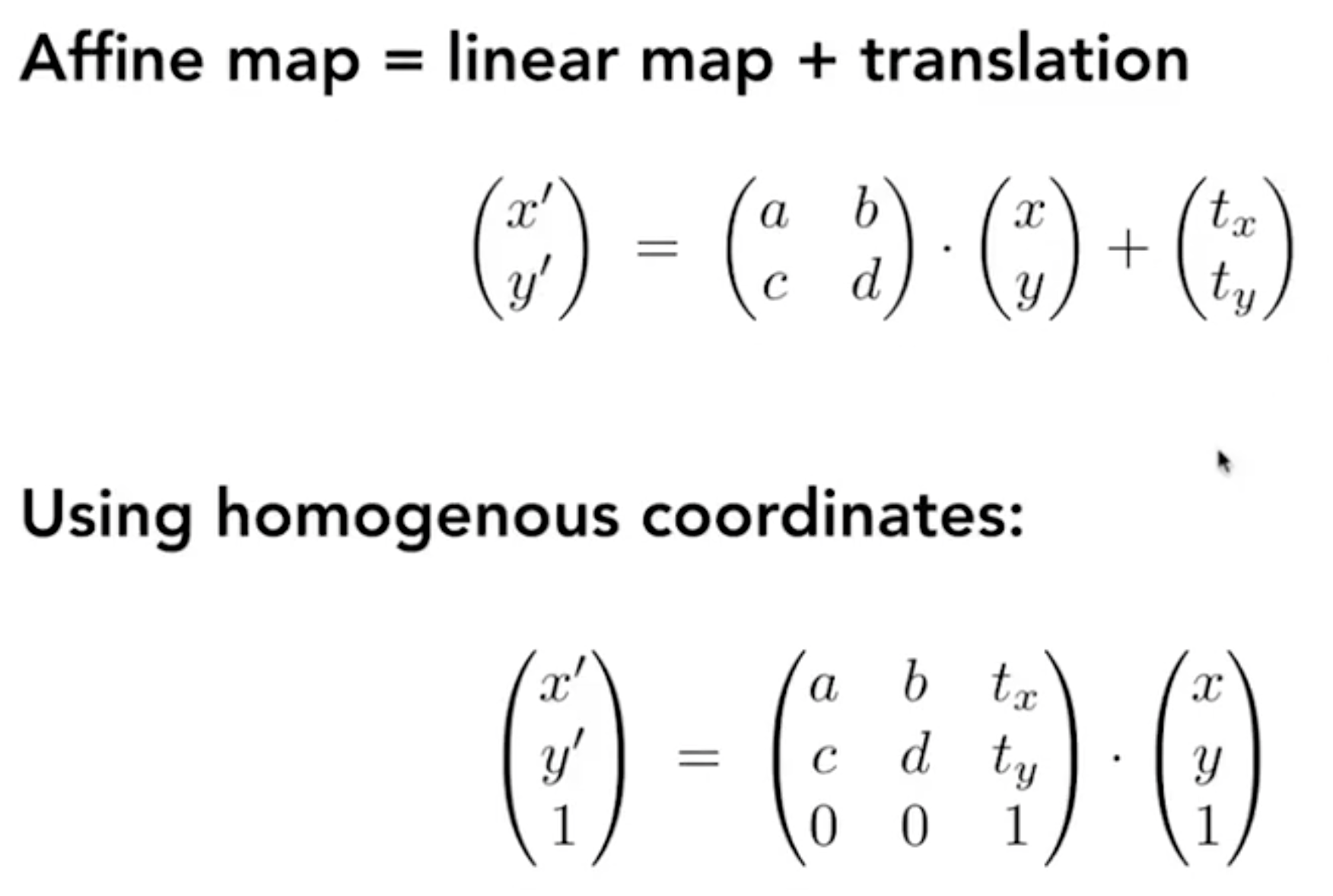
    • 截屏2023-03-26 21.29.32
    • $\begin{pmatrix}线 & 性 & 平\\ 变 & 换 & 移\\ 0&0&1 \\ \end{pmatrix}$
  • 逆变换
  • 复合变换：分步左乘变换矩阵，不满足交换律
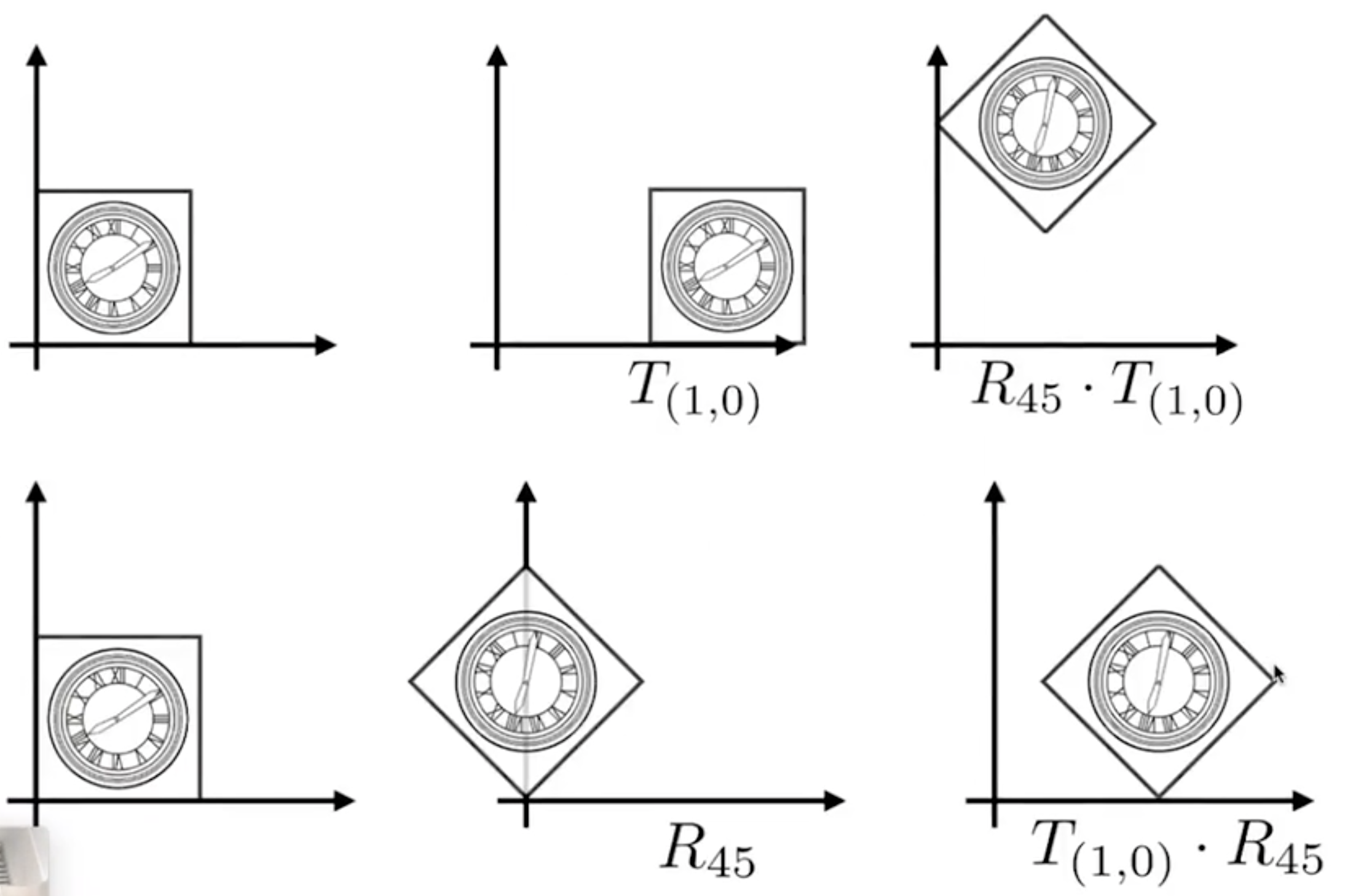
    • 截屏2023-03-26 21.42.15
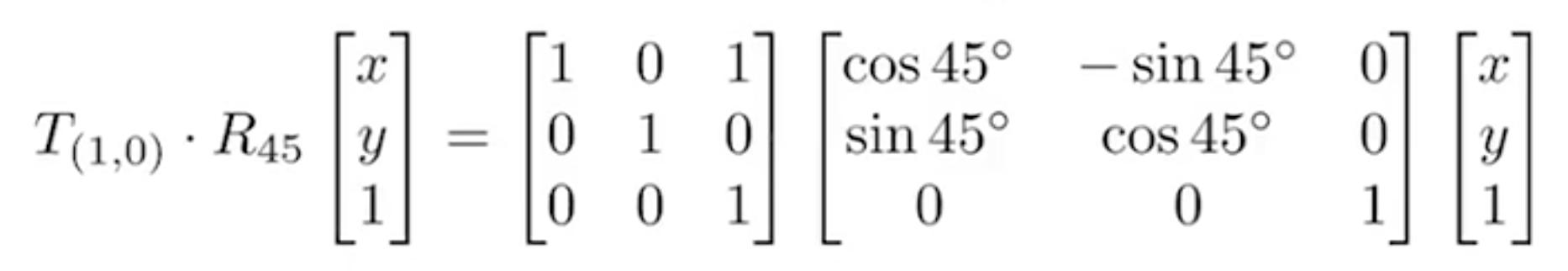
    • 截屏2023-03-26 21.43.20
      • 先应用线性变换，再平移

3D Transformation

  • 引入其次坐标
    • $3D\quad point = (x, y, z, 1)^T$
    • $3D \quad vector = (x, y, z, 0)^T$
  • 仿射变换
    • 截屏2023-03-27 10.03.04

P4

3D Transformation

  • 三维空间旋转
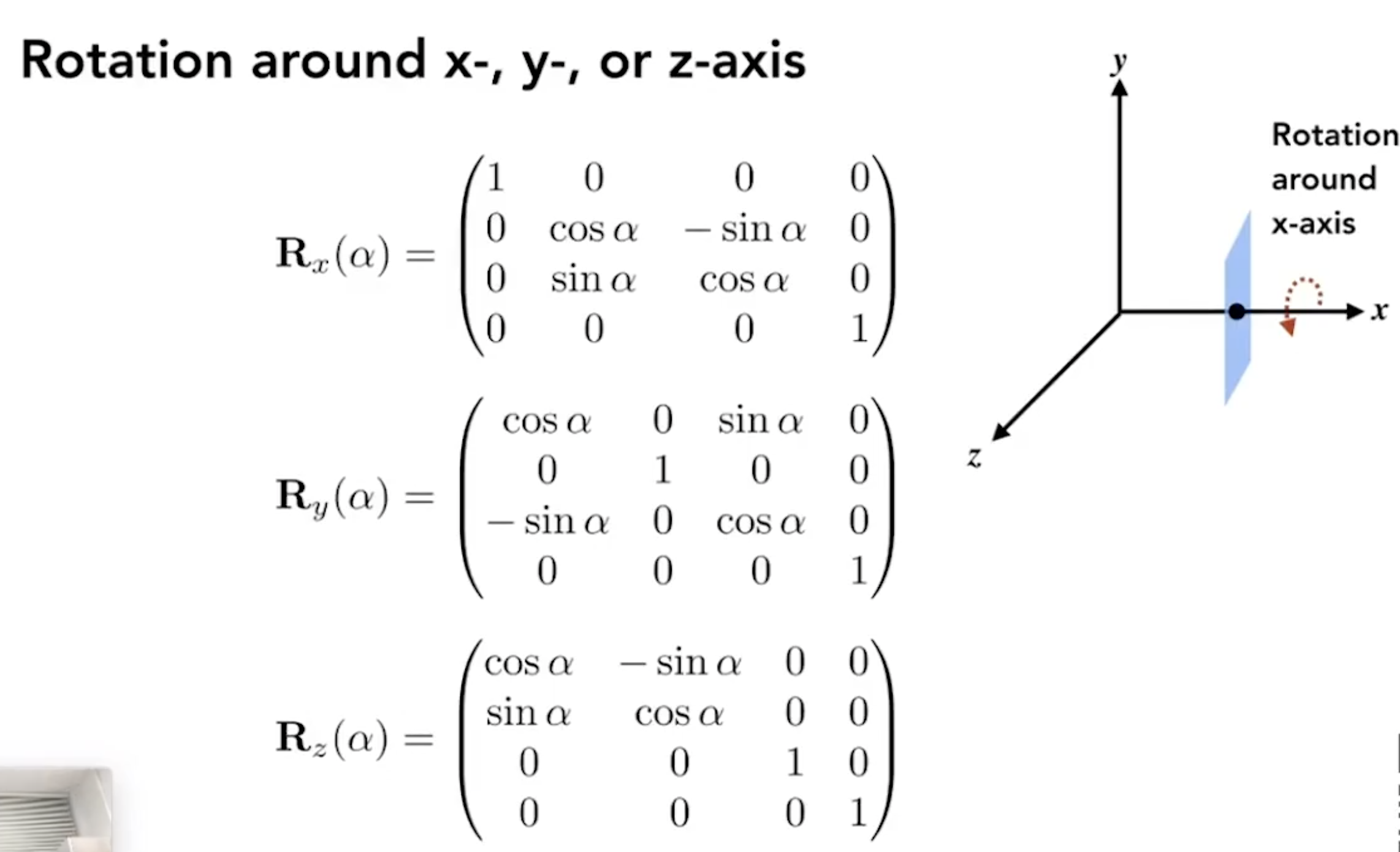
    • 截屏2023-03-27 10.27.29
      • Y轴旋转相反：X ✖️ Z = -Y
    • $R_{xyz}(\alpha, \beta ,\gamma) = R_x(\alpha)R_y(\beta)R_z(\gamma)$ 三维空间变换分解
      • $\alpha$, $\beta$ ,$\gamma$ 为欧拉角
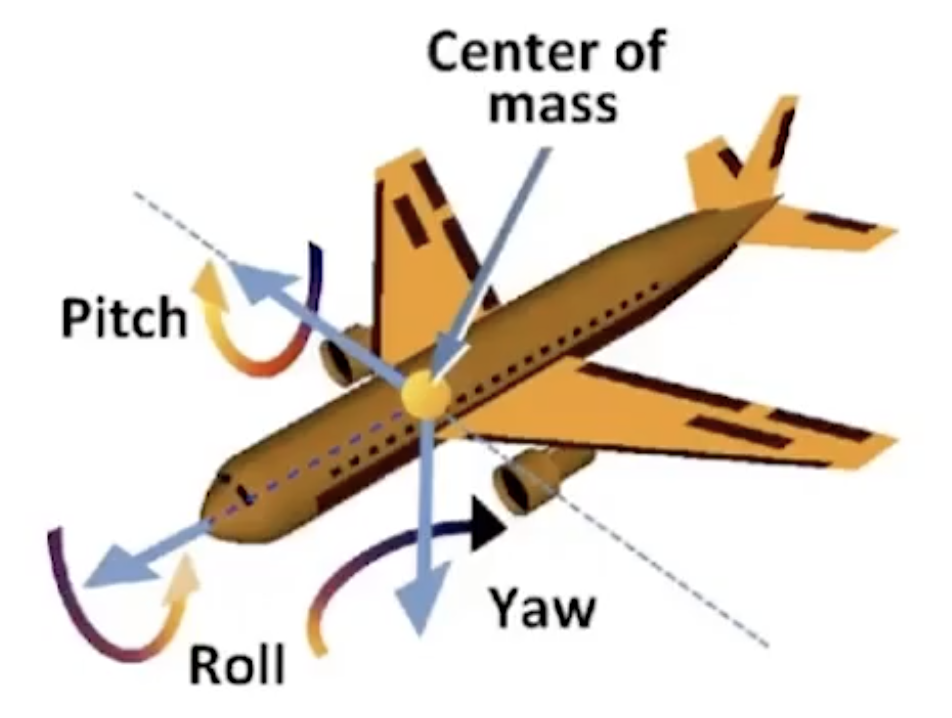
      • Yaw, Pitch, Roll描述三维空间变换
        • 截屏2023-03-27 10.37.26
    • 罗德里格斯旋转公式：绕n轴旋转$\alpha$
      • 截屏2023-03-27 10.40.09

Viewing Transformation 视图变换

得到$[-1, 1]^3$的立方体

View/Camera Transformation

  • MVP变换
    • 截屏2023-03-27 10.52.32
  • How to perform view transformation? 得到$M_{view}$视图变换矩阵
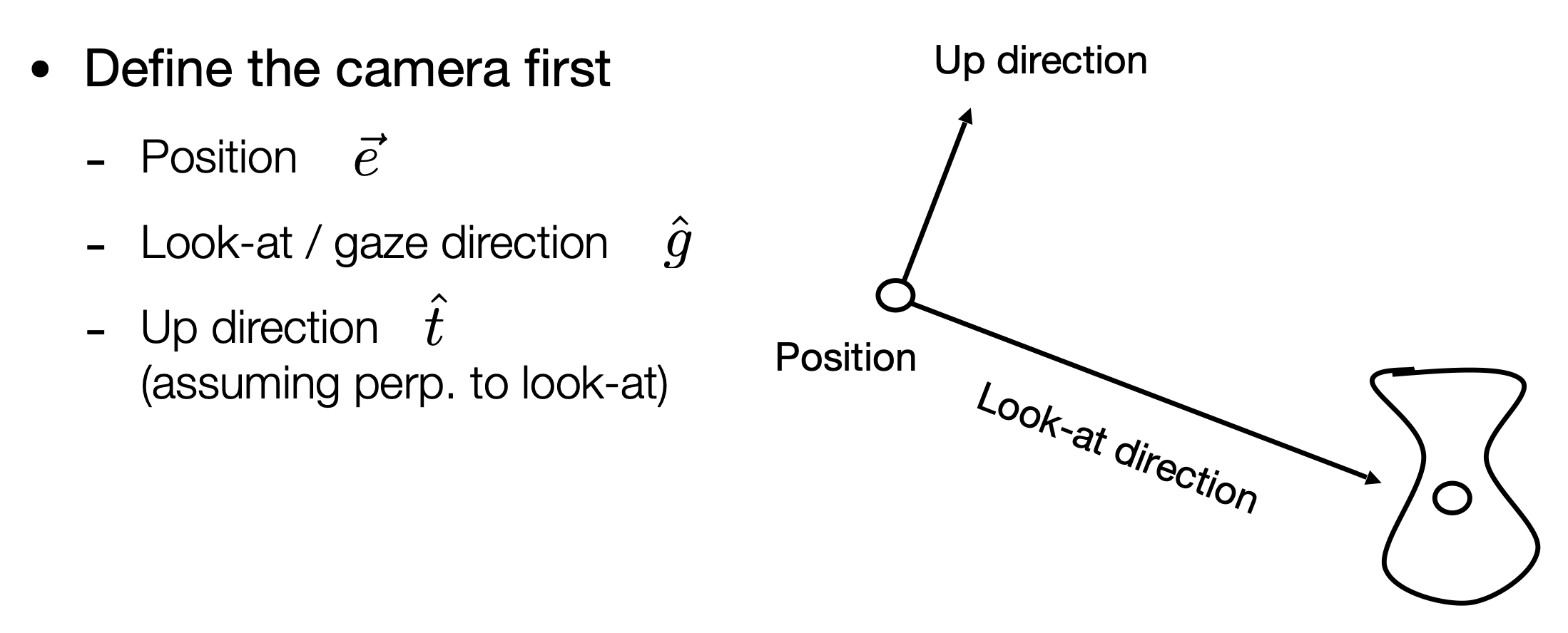
    • 截屏2023-03-27 10.56.48
      • Up Direction：用一个向量定义相机向上的方向
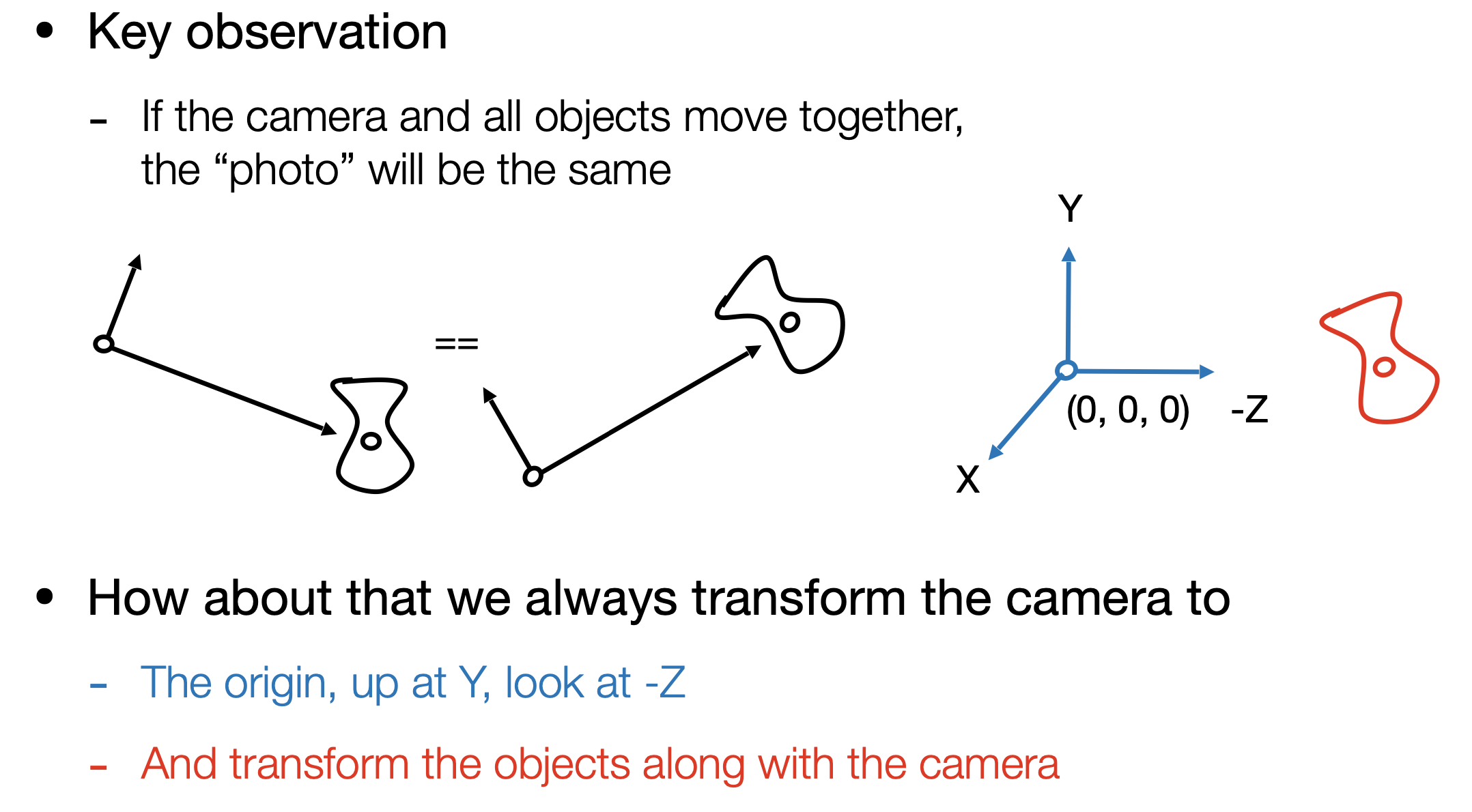
    • 截屏2023-03-27 10.57.15
      • 相机放在标准位置(0, 0, 0)，向-Z看，上方向为Y
    • 实现上一步的步骤
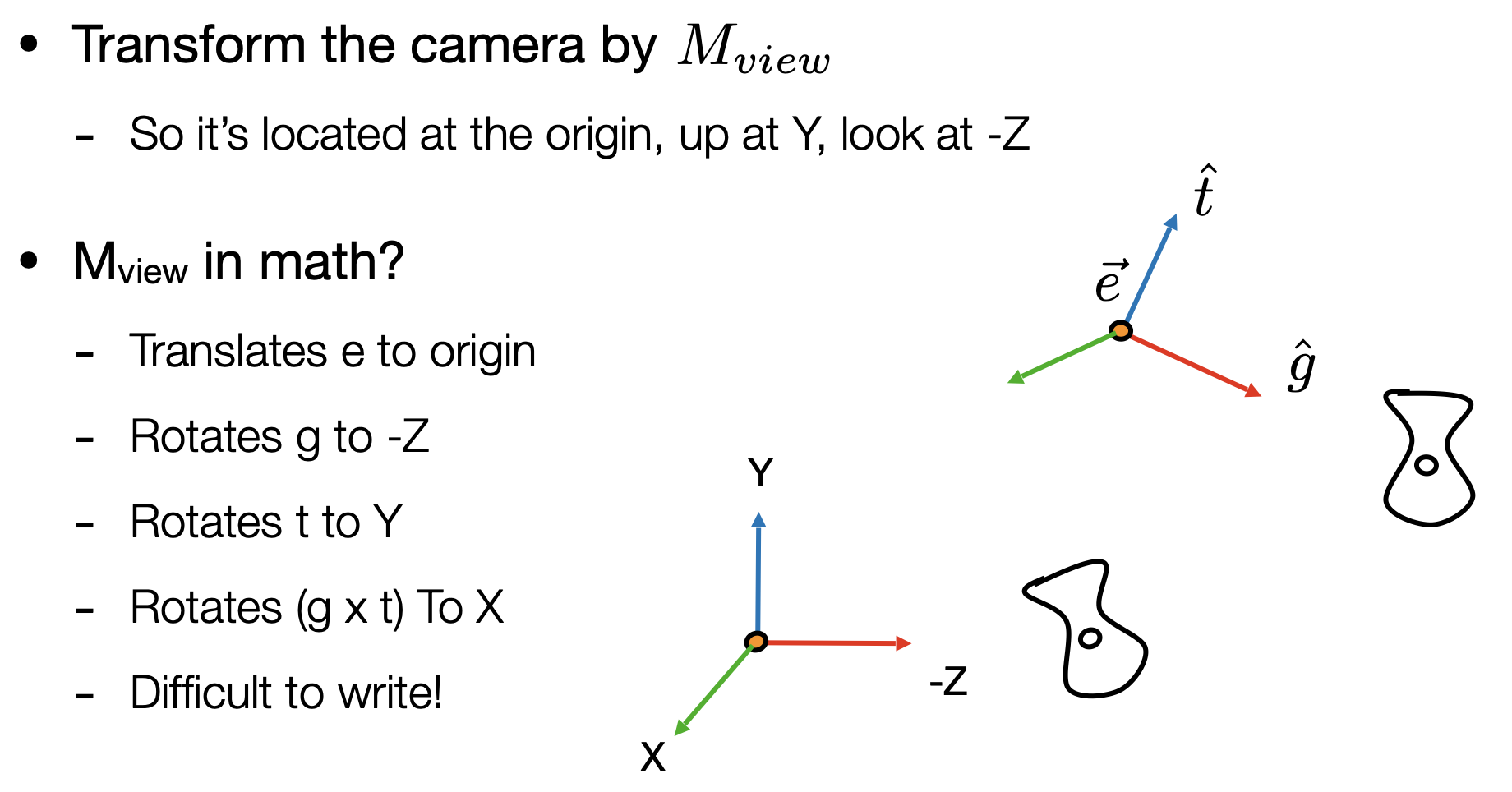
      • 截屏2023-03-27 11.03.25
      • 截屏2023-03-27 11.05.16
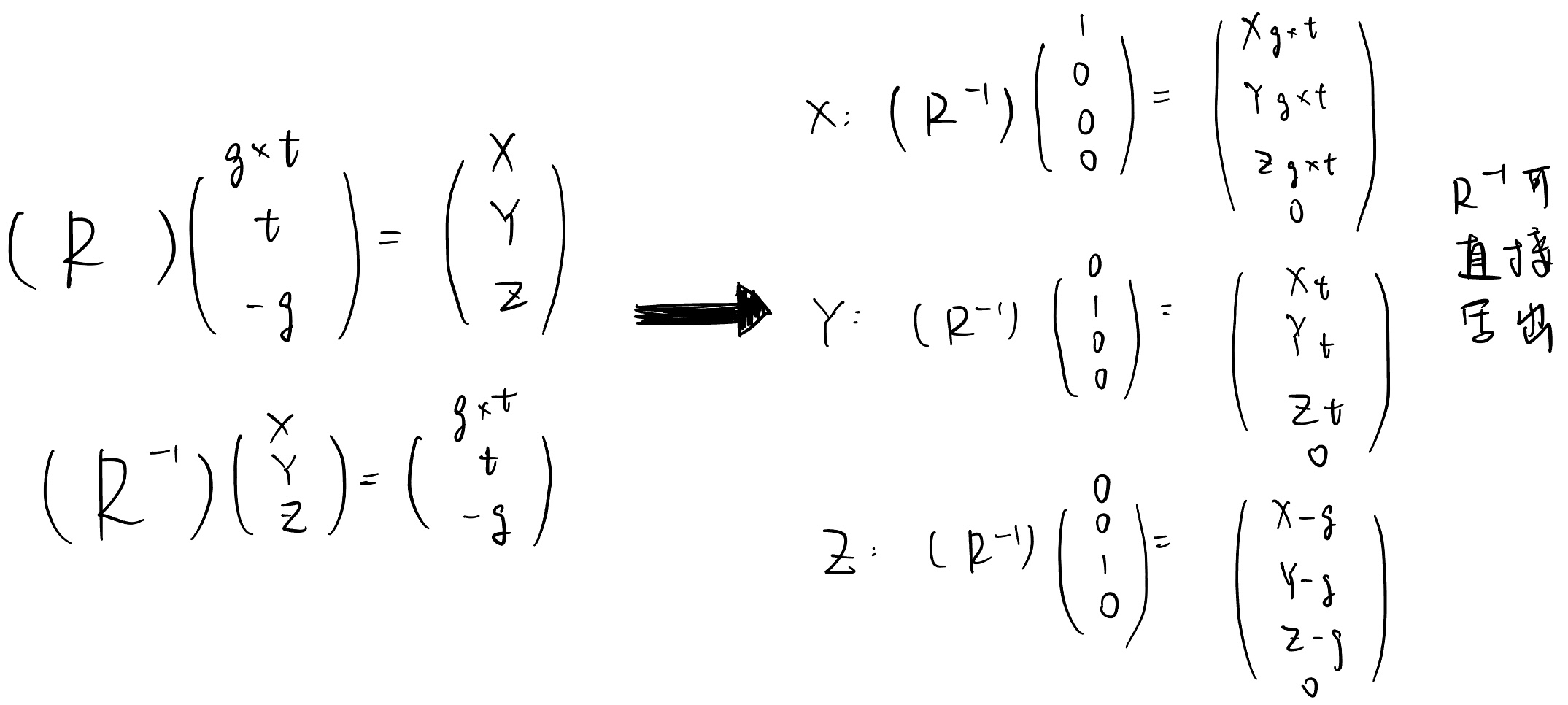
        • R~view~^-1^：将xy -z旋转到etg（代入X(1,0,0,0)^T^, Y(0,1,0,0)^T^, Z(0,0,1,0)^T^可以验证XYZ向量的旋转得到etg）IMG_0776
        • 正交矩阵，逆 = 转置
    • 总结
      • $M_{view}$视图变换操作相机，其他物体跟着相机发生变换
      • 得到的结果：相机在原点，朝向-Z，上方向为Y
    • ModelView Transformation模型视图变换：移动相机模型跟着变换，Model和View可相提并论

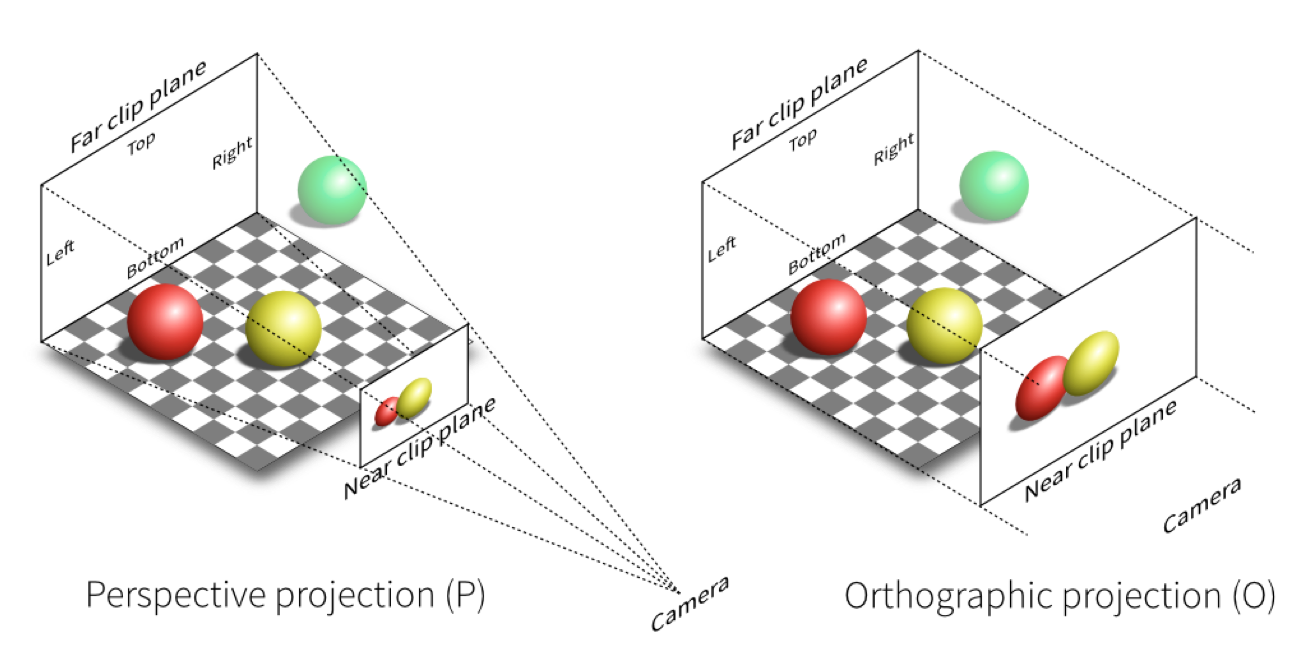
Projection Transformation

  • Ortho vs. Persp
    • 截屏2023-03-27 14.02.28
Orthographic Projection正交投影
  • 简单做法
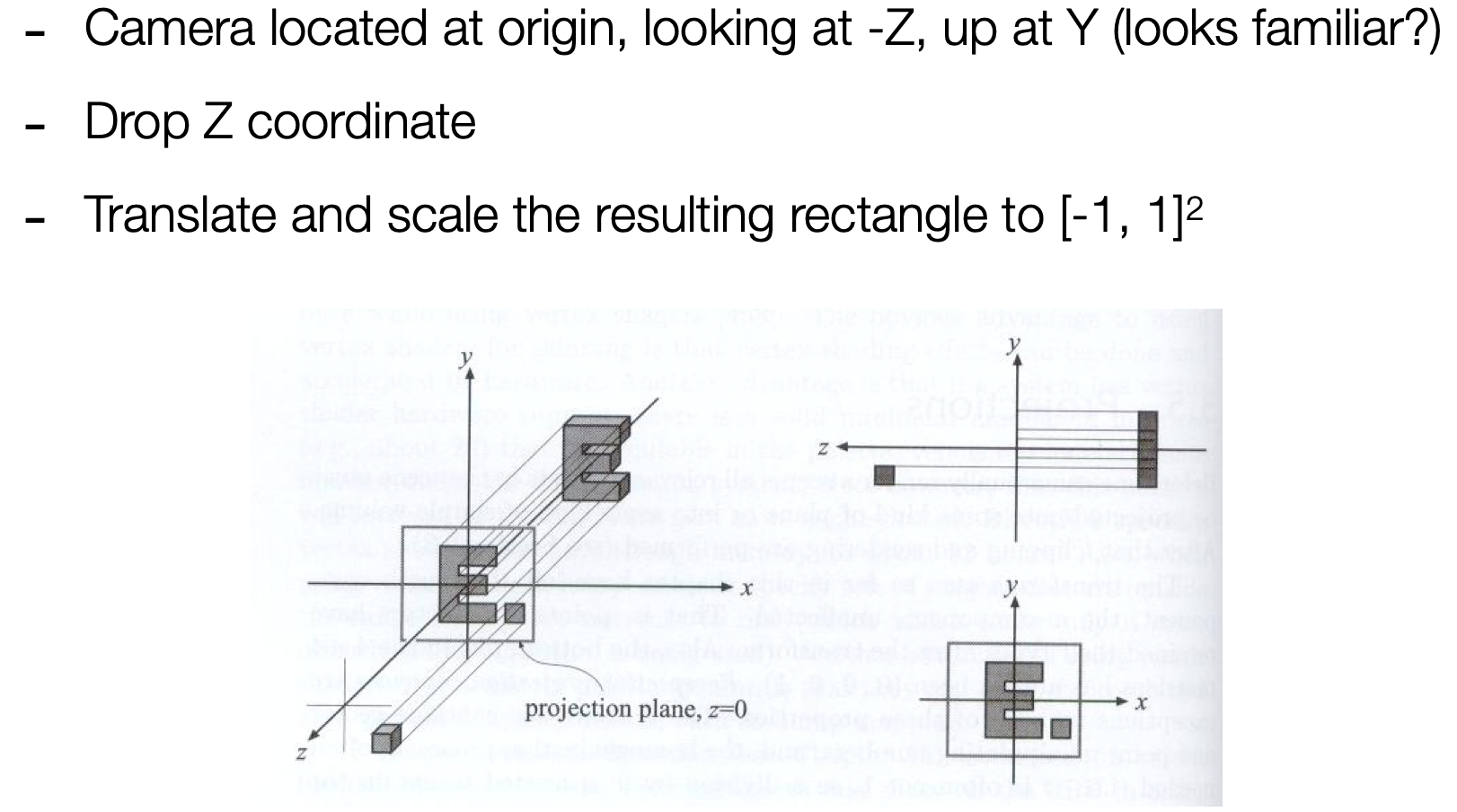
    • 仍掉Z 截屏2023-03-27 14.05.51
  • 正式做法
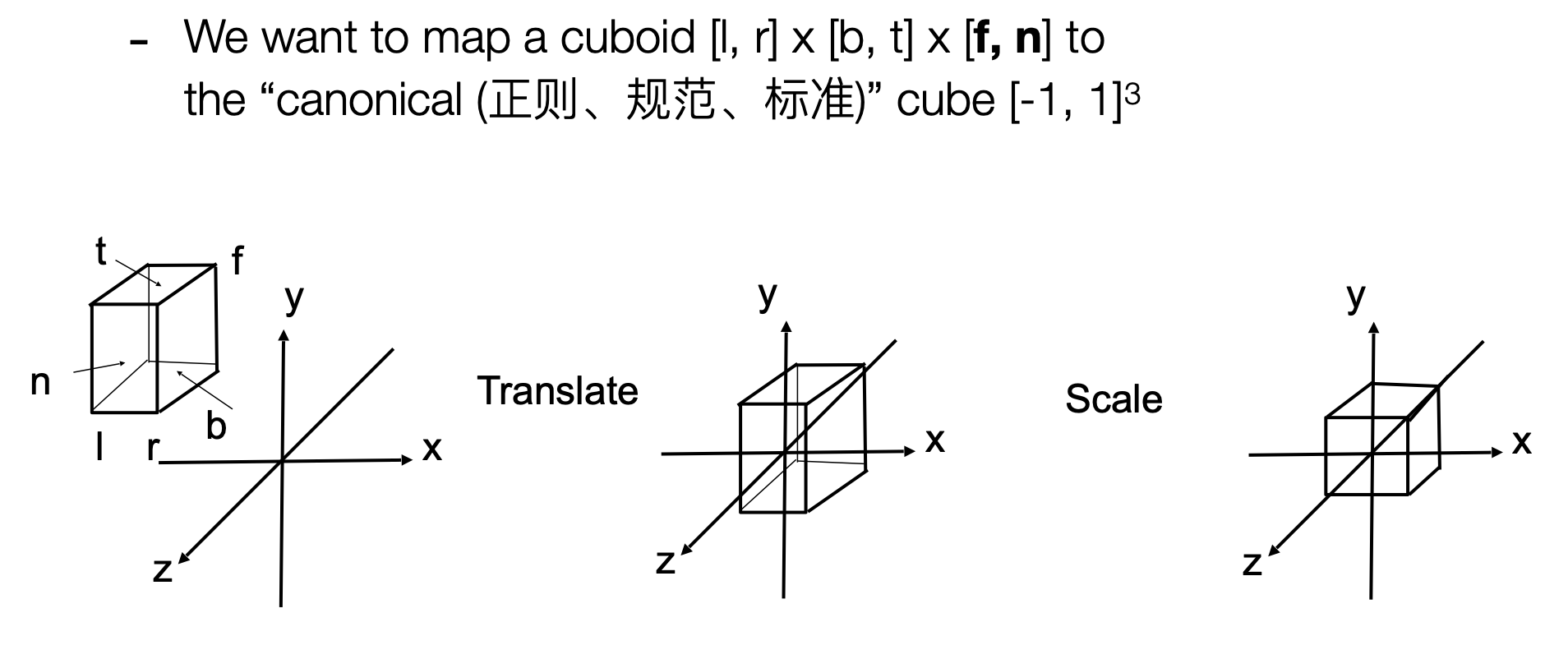
    • 截屏2023-03-27 14.14.53
      • 定义立方体（三个轴的范围）
      • 将立方体中心移到原点
      • 映射到$cube[-1, 1]^3$
  • $M_{ortho}$正交变换矩阵
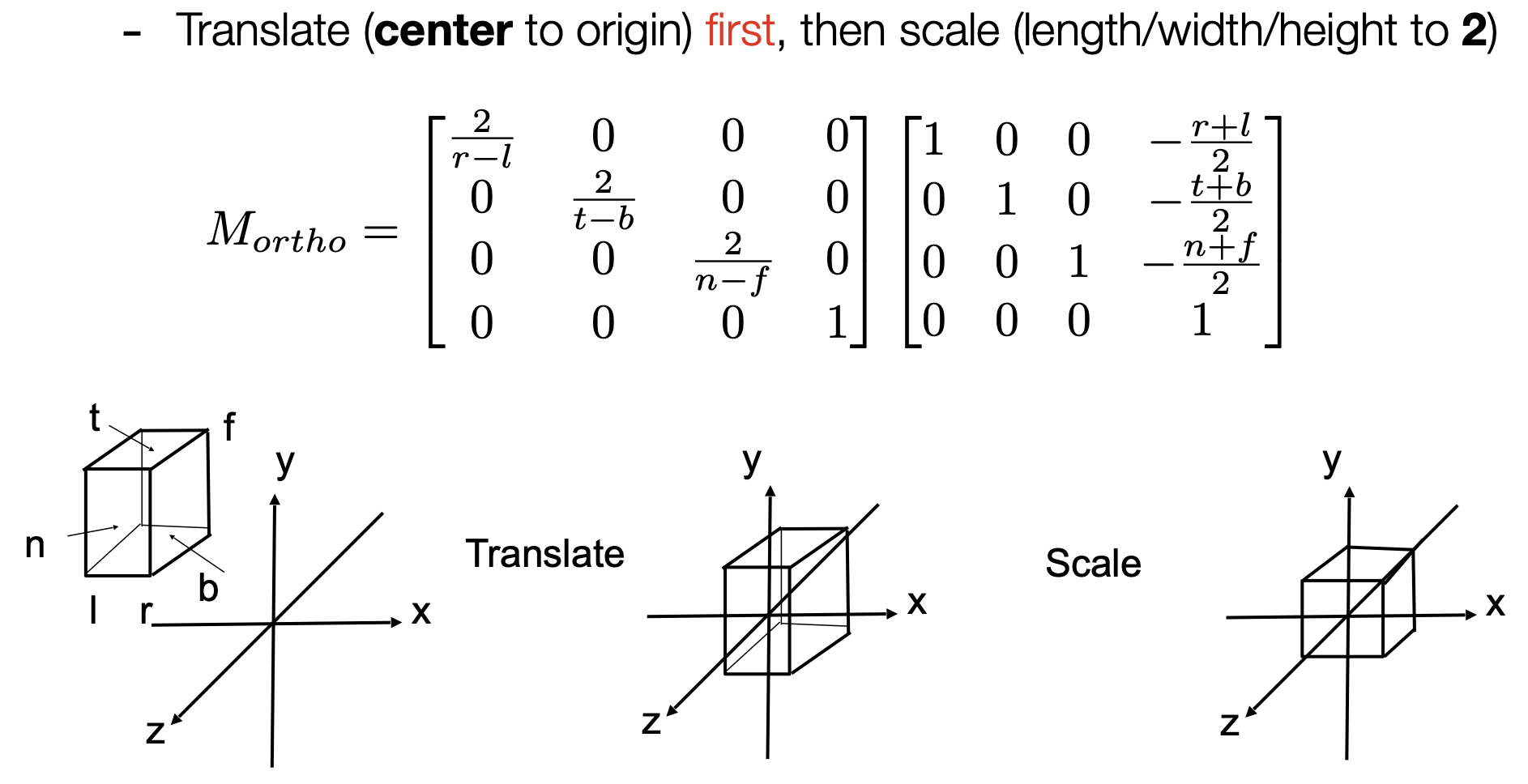
    • 截屏2023-03-27 14.18.21
      • 先平移，再缩放
  • 注意⚠️
    • 这里使用右手系。看向-Z方向，所以n平面(近处)的Z数值比f平面(远处)大
Perspective Projection 透视投影
  • 知识回顾
    • 截屏2023-03-27 14.32.51
  • 步骤
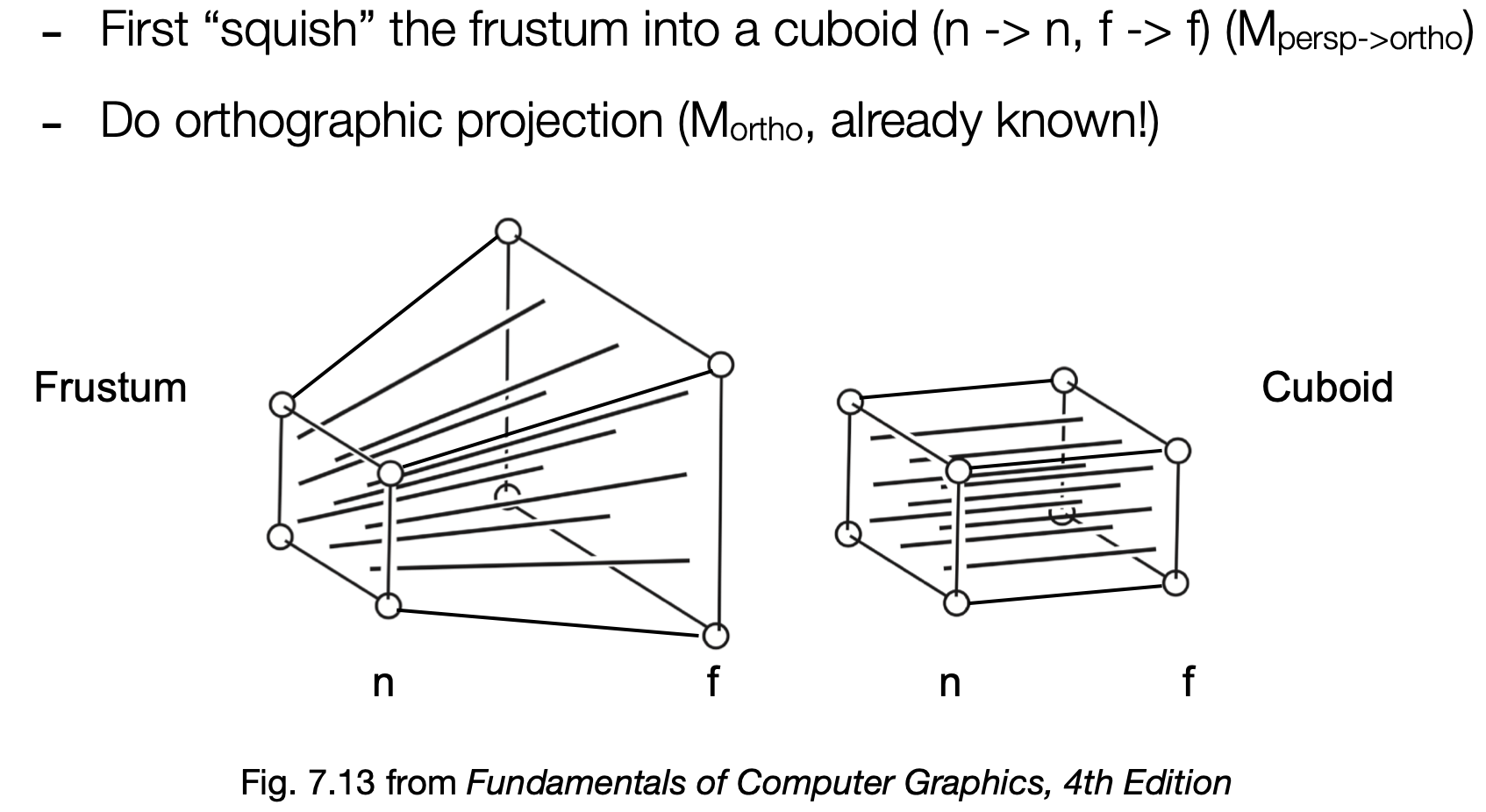
    • 概述：截屏2023-03-27 14.33.45
      • 将视锥远平面压缩到长方体中（$M_{persp->ortho}$）
        • 近平面永远不变
        • 远平面中心点不变，Z不变
      • 长方体做正交投影（$M_{ortho}$）
    • STEP1：将persp视锥远平面压缩到ortho长方体中，xy可通过相似三角形计算，z未知
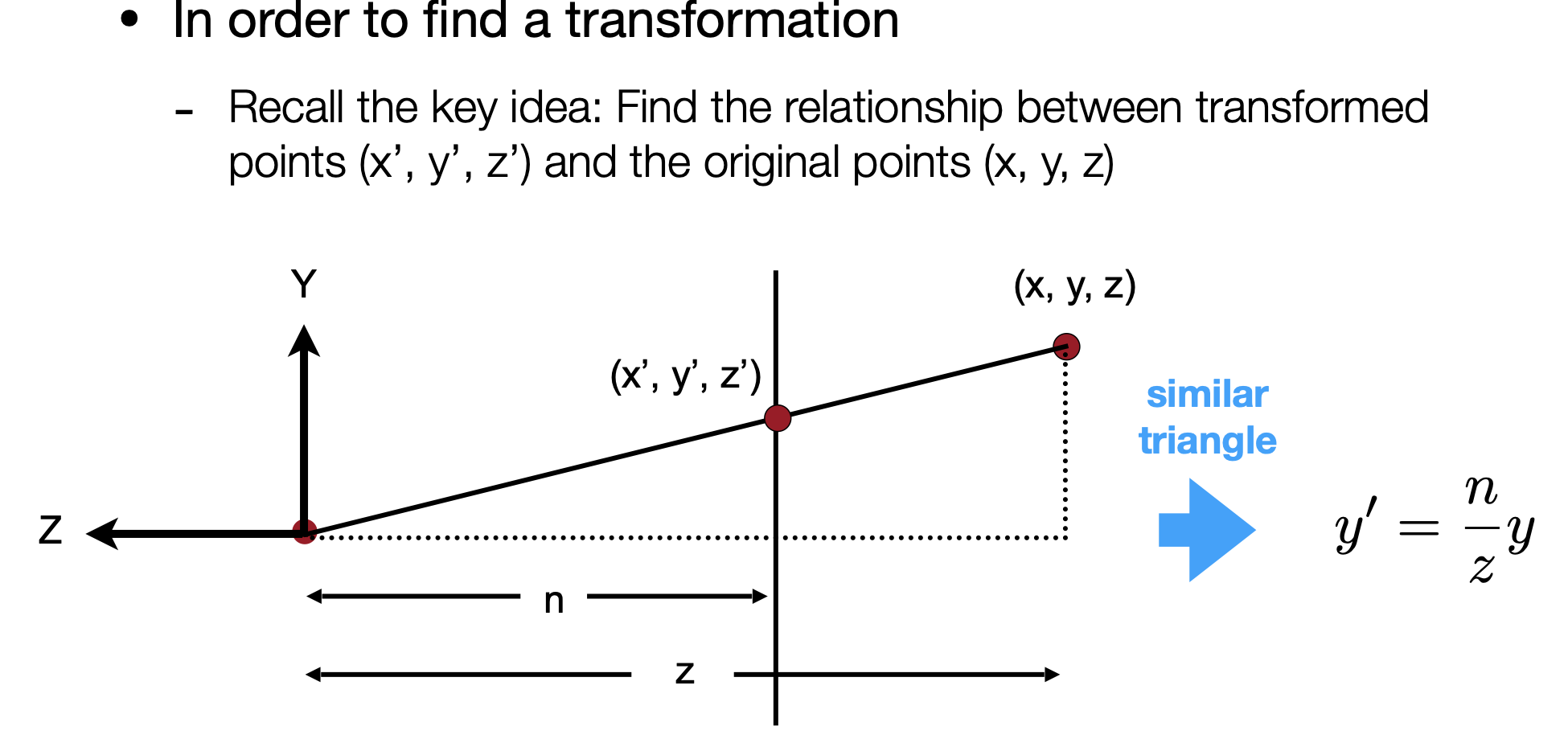
      • 关于Y如何被挤压截屏2023-03-27 14.41.45
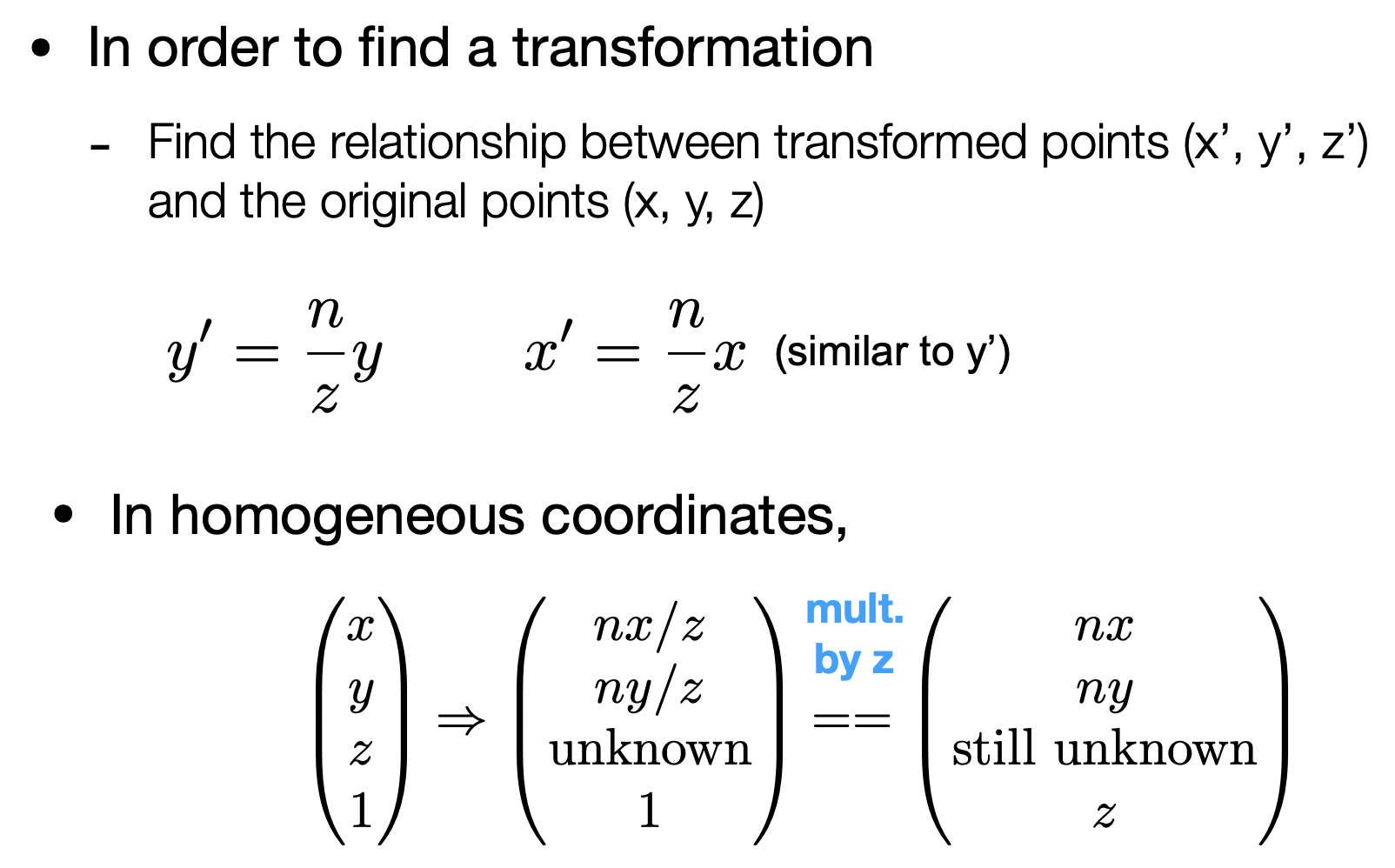
      • 截屏2023-03-27 14.44.02
      • 截屏2023-03-27 14.50.43
        • 利用近平面的点(x, y, n, 1)，特殊化求解第三行
          • 下图右上角：$(x,y,n,1)^T$经$M_{persp->ortho}$变换后，还是会得到自己本身。因此乘n，得到与左上角格式类似的矩阵（此时的z=n），可看到unknown的值在近平面为$n^2$
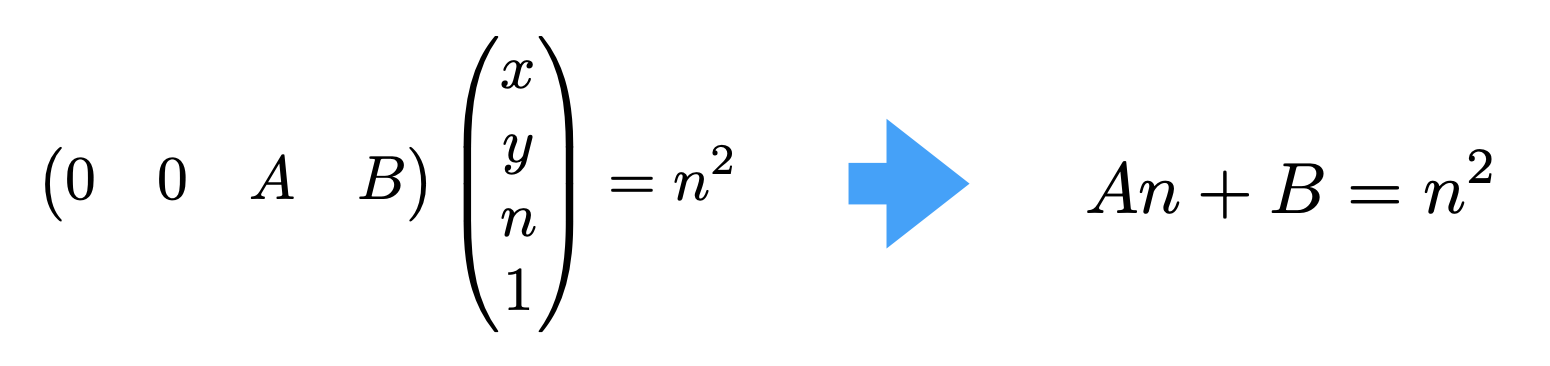
          • 截屏2023-03-27 14.56.24截屏2023-03-27 14.57.10
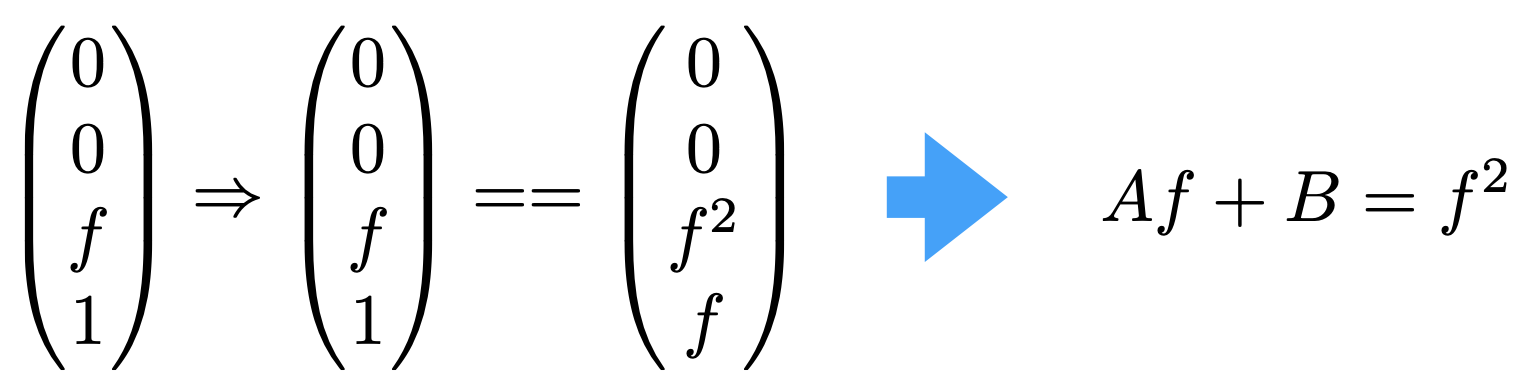
        • 利用远平面中点(0, 0, f, 1)不变截屏2023-03-27 14.58.40
        • 截屏2023-03-27 15.14.45
        • $M_{persp->ortho} = \begin{pmatrix}n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f &-nf \\ 0 & 0 & 1& 0 \\ \end{pmatrix}$
    • STEP2：对压缩后长方体进行$M_{ortho}$
      • 截屏2023-03-27 15.15.03