Games101-P5-6 Rasterization
- P5 Preview
- Finishing up viewing
- Viewport transformation
- Rasterization
- Different raster displays
- Rasterizing a triangle
- Finishing up viewing
P6 Preview
Antialiasing
- 采样简单理论
- 实际图形学中的反走样
Visible / Occlusion(讲解部分在P7开始处)
- Z - Buffer
补充!
- shadows
P5 Rasterization(Triangles)
Finishing up viewing
Viewport transformation 视口变换
Intro - 摄影机
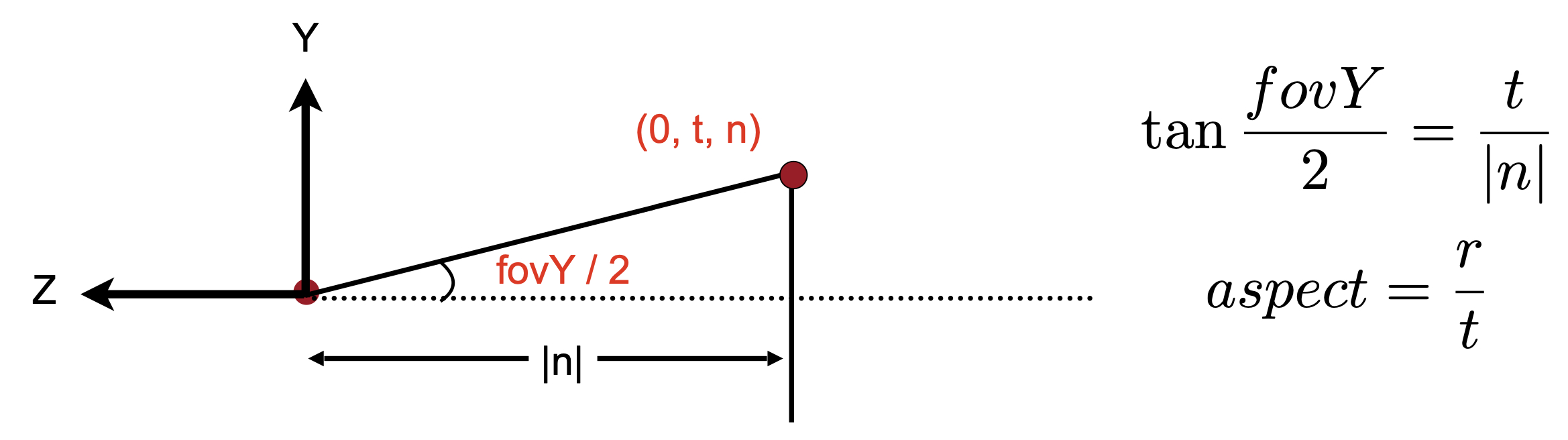
- 定义视锥的两个概念
- 长宽比
- FOV
- 用近平面lrbt表示fov
- What’s after MVP?
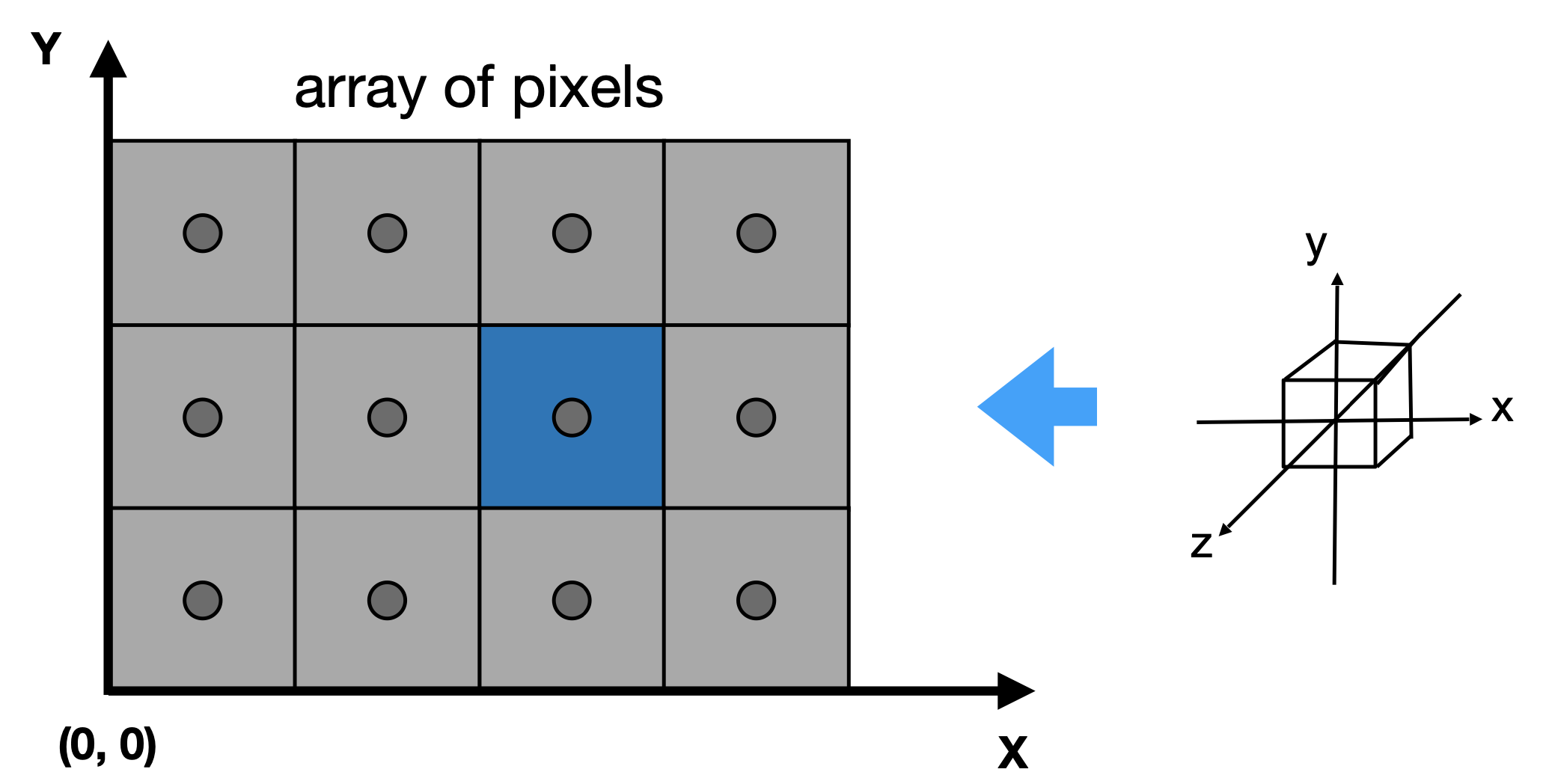
Intro - 屏幕
- 什么是屏幕
- 抽象地认为是二维数组,其中每个元素都是一个像素
- 数组的大小就是屏幕分辨率
- 一种典型的光栅化显示
- Raster光栅
- Rasterize == drawing onto the screen
Pixel像素
- 课程中简单地认为是一个个小方块
- 实际是RGB的空间混合
定义屏幕空间
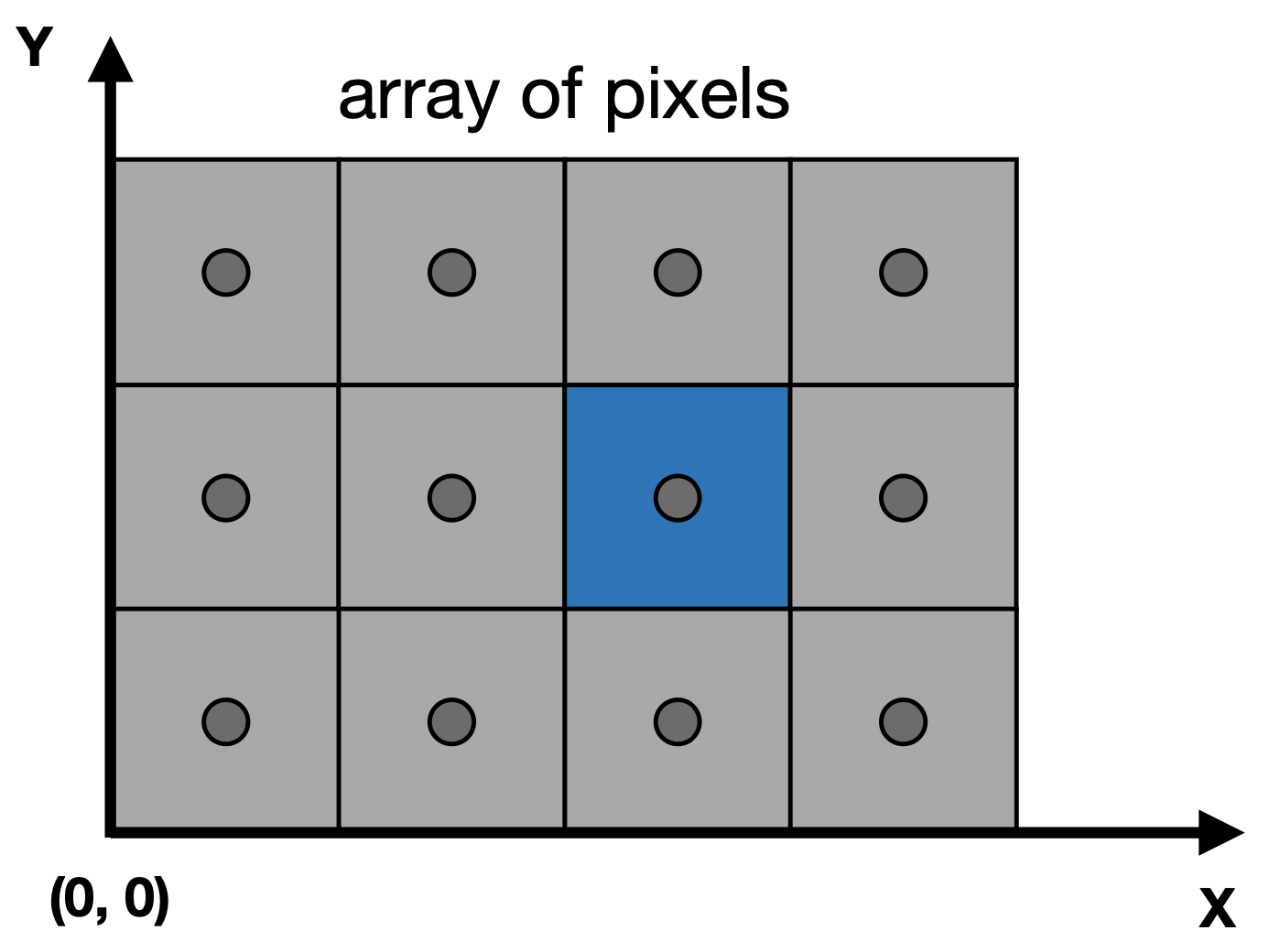
- (x,y)形式,每个像素坐标均为整数。蓝色坐标为(2,1),因为从0开始
- 屏幕上,像素坐标范围是(0,0)到(width - 1,height - 1)
- 像素中心坐标是(x+0.5,y+0.5)
- 屏幕范围(0,0)到(width,height)
视口变换:将$[-1, 1]^3$立方体转化到整个屏幕
- Transform xy plane: $[-1, 1]^2$ to $[0 ,width] * [0, height]$,先不管$z$
- 视口转化矩阵
- $M_{viewport} = \begin{pmatrix} \frac{width}2 & 0 & 0 & \frac{width}2\\ 0& \frac{height}2 & 0 & \frac{height}2 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0& 1 \\ \end{pmatrix}$
- 左上角矩阵缩放
- 缩放后原点是中心,需将左下角平移到原点
- $M_{viewport} = \begin{pmatrix} \frac{width}2 & 0 & 0 & \frac{width}2\\ 0& \frac{height}2 & 0 & \frac{height}2 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0& 1 \\ \end{pmatrix}$
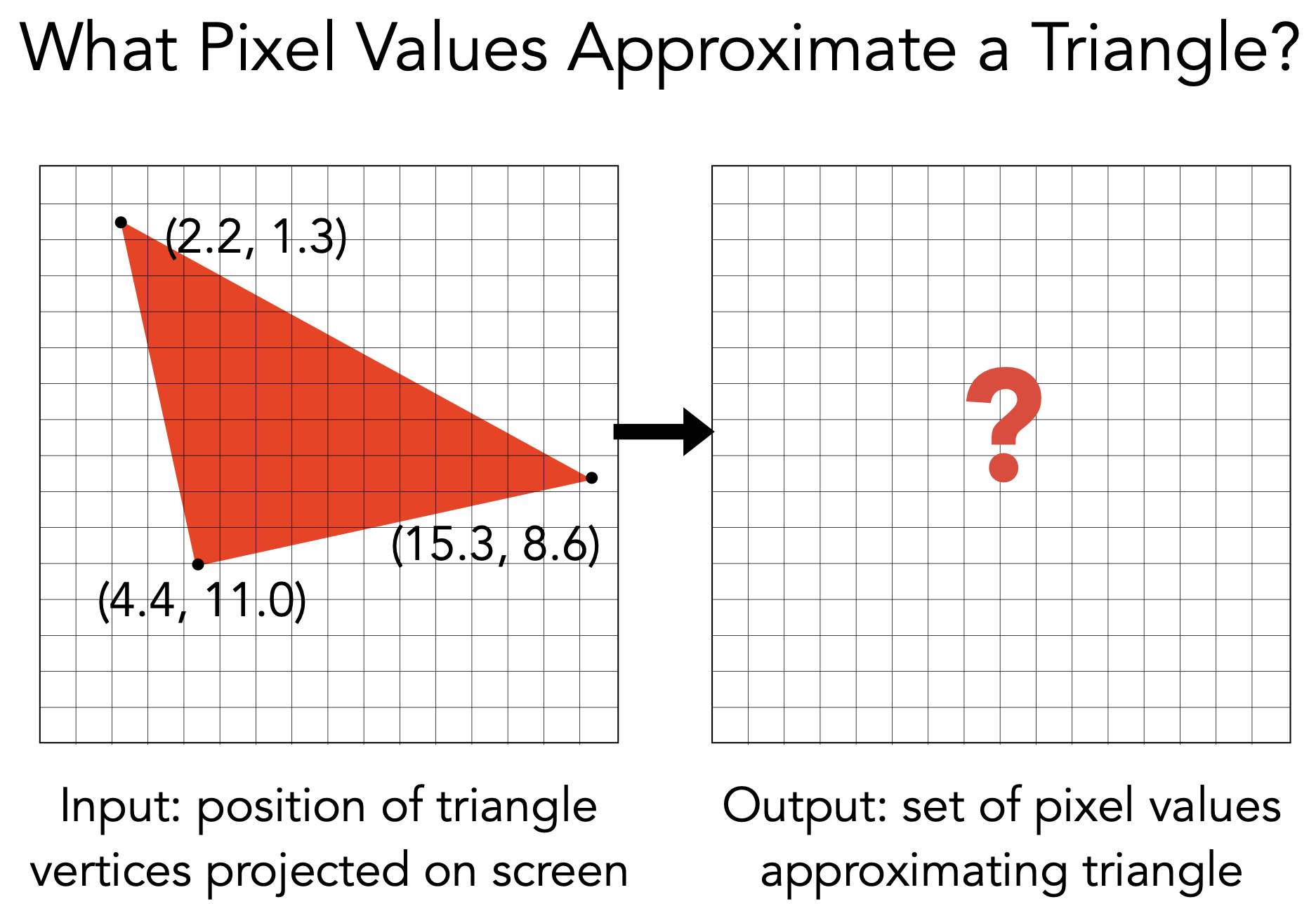
光栅化 - Rasterizing Triangles into Pixels
Frame Buffer: Memory of a Raster Display
- 内存空间的一块区域映射到屏幕上,成为显示的图像
Polygon Mesh
- intro
- 已完成:将三维空间顶点变换到屏幕空间中
- 下一步:将多边形拆成不同的像素(光栅化的过程
- Triangle Mesh
- 基础性质
- 最基础的多边形
- 任何其他多边形都可拆成三角形
- 独特性质
- 三角形三点必在同一平面
- 三角形内外定义清晰(可以通过叉积直接定义三角形内外
- 三角形内部的点,可根据已知三个点的信息进行渐变(lerp插值)
- 基础性质
Sampling 采样
采样函数(一维
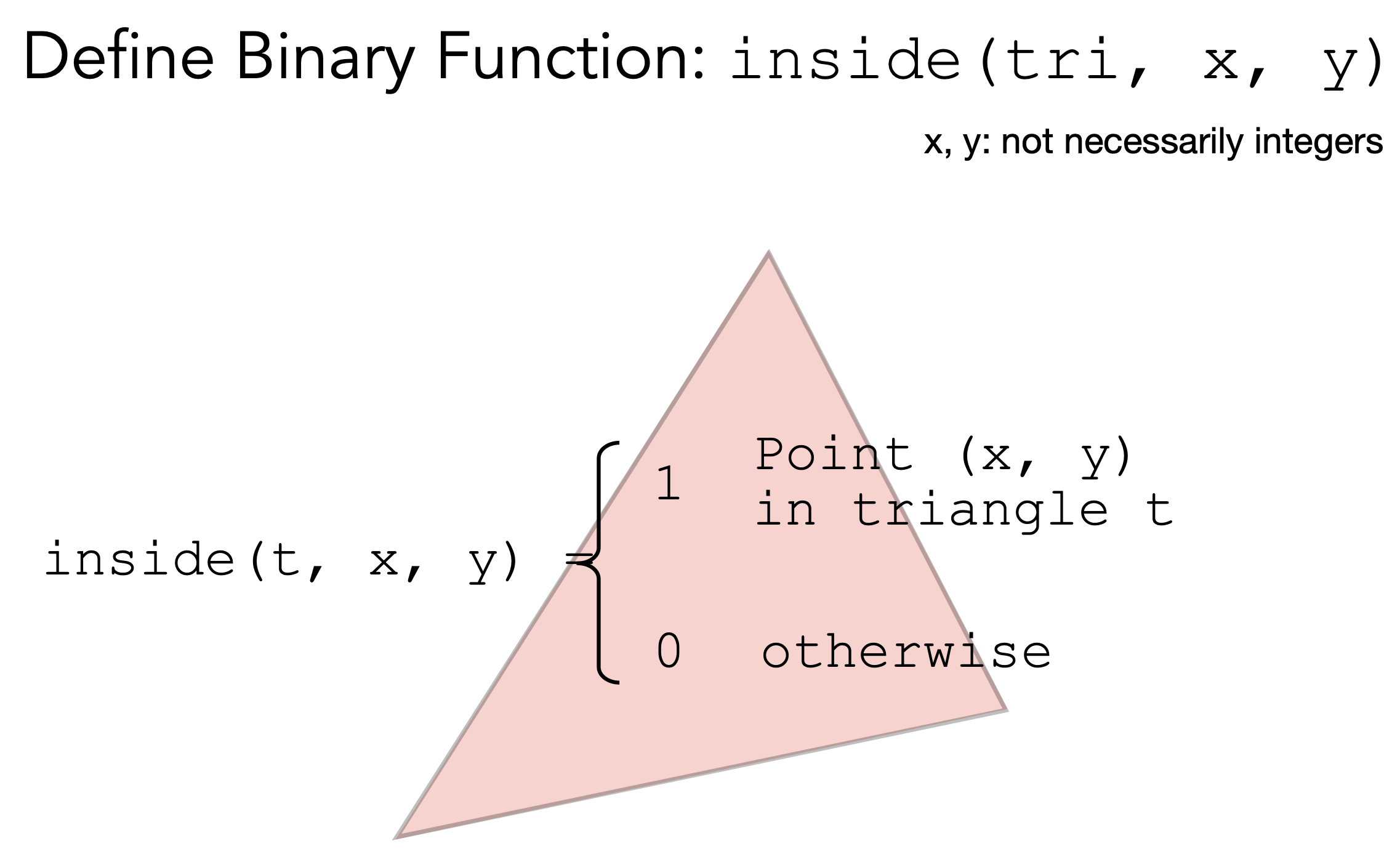
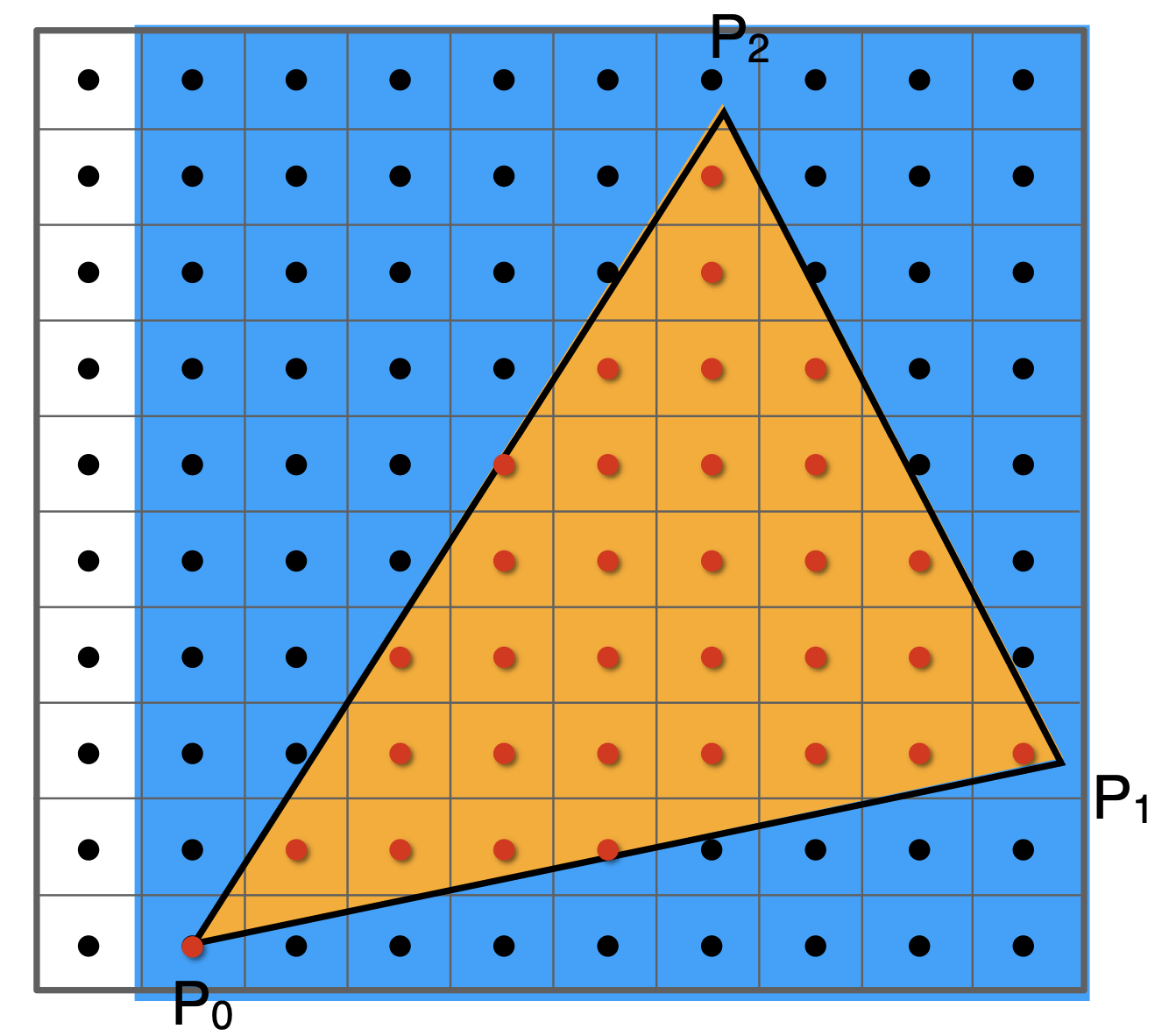
判断像素中心是否在三角形内
二维采样
for (int x = 0; x< xmax; x++) for (int y = 0; y < ymax; y++) image[x][y] = inside(tri, x + 0.5, y+ 0.5); //三角形中心要+0.5
inside(tri, x, y)具体如何实现:向量叉积
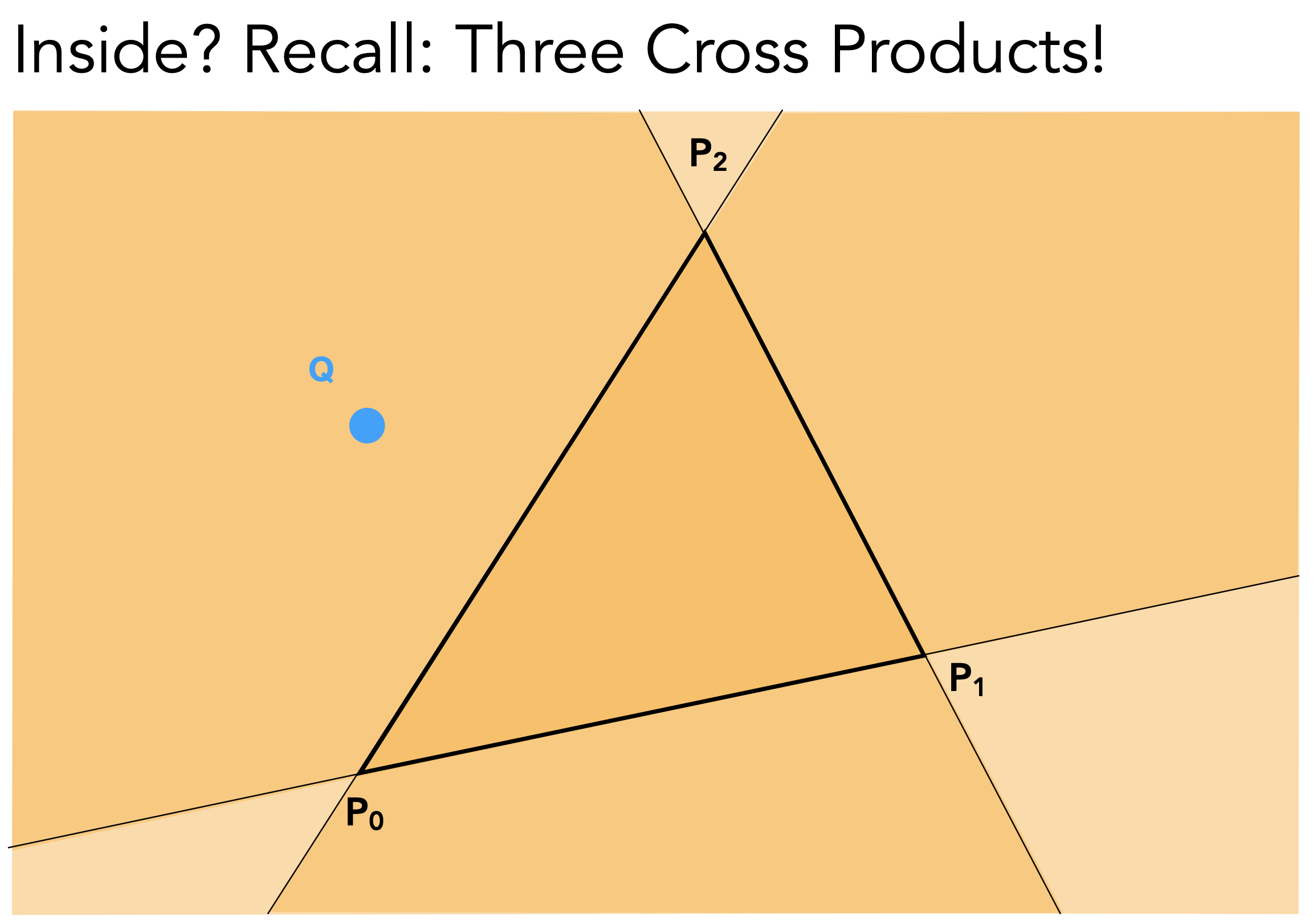
- $\overrightarrow{P_1P_2} \times \overrightarrow{P_1Q}$ 得到$Q$在$P_1P_2$左边,$P_0P_1$同理
- $\overrightarrow{P_2P_0} \times \overrightarrow{P_2Q}$ 得到$Q$在$P_2P_0$右边
- 综上,$Q$在三角形外
边界处理:OpenGL认为上左在内,下右在外
光栅化加速优化
- 包围盒Bounding Box(AABB)
- 每一行只考虑最左和最右,相当于一行一个Bounding Box
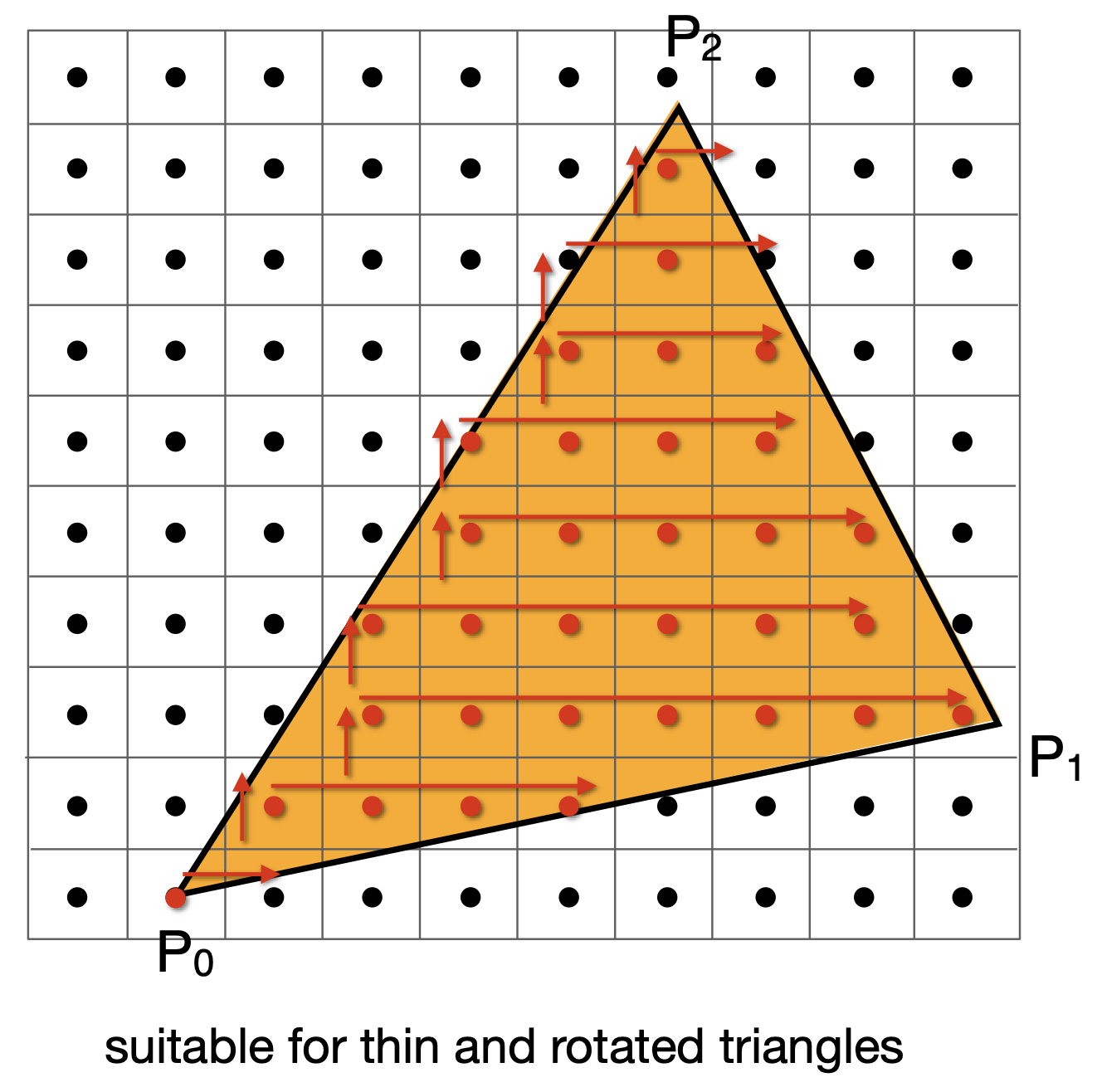
- 适用于瘦长三角形
实际屏幕的光栅化 Rasterization on Real Displays
- 加色
- 减色
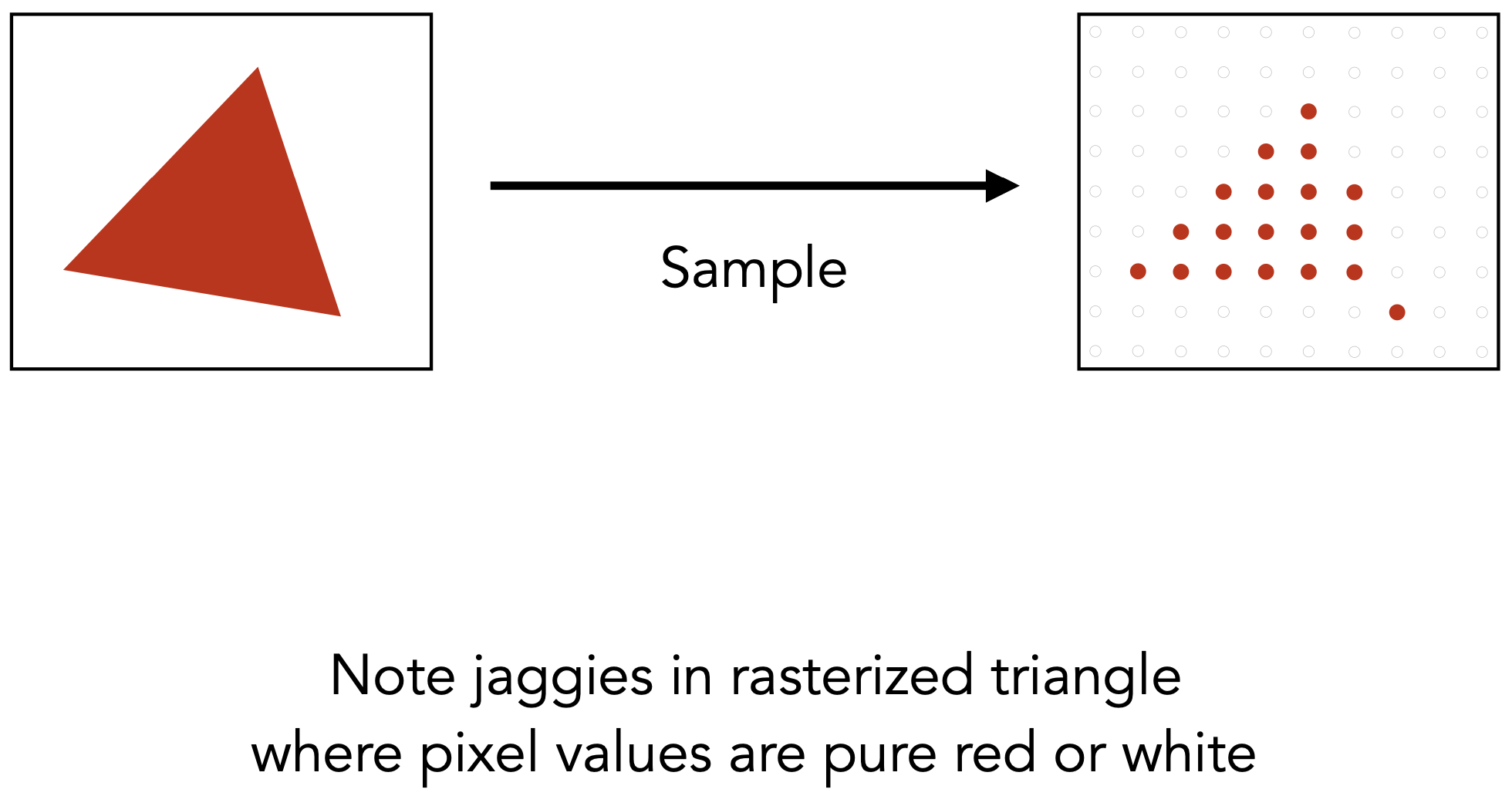
光栅化问题
- 锯齿
- 像素有一定大小,采样率不够高,导致图像走样
P6 Rasterization(Antialiasing and Z-Buffer 反走样和深度缓冲)
采样理论
- Artifact:黑话。泛指图形学中的error/mistake/inaccuracies
- 锯齿
- 摩尔纹
- 车轮倒转效应
- 产生Artifact的本质原因:信号速度太快,而采样速度跟不上
如何反走样
- 基本思想:前进行Blur,本质是滤(高频)波;再进行采样
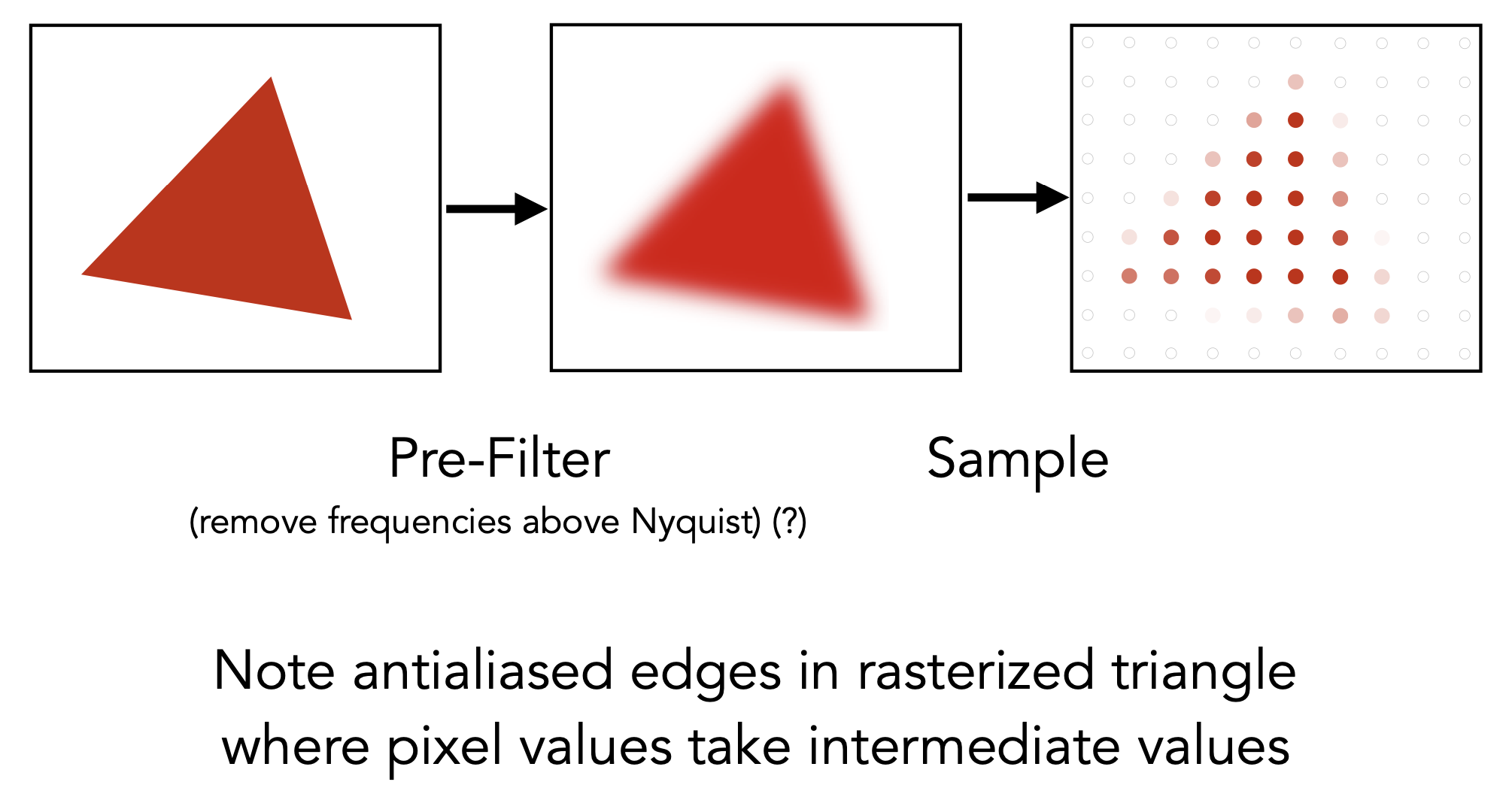
- 不可以先采样,再滤波(先采样的话,混叠的信号已然存在,再进行滤波也无法消除)
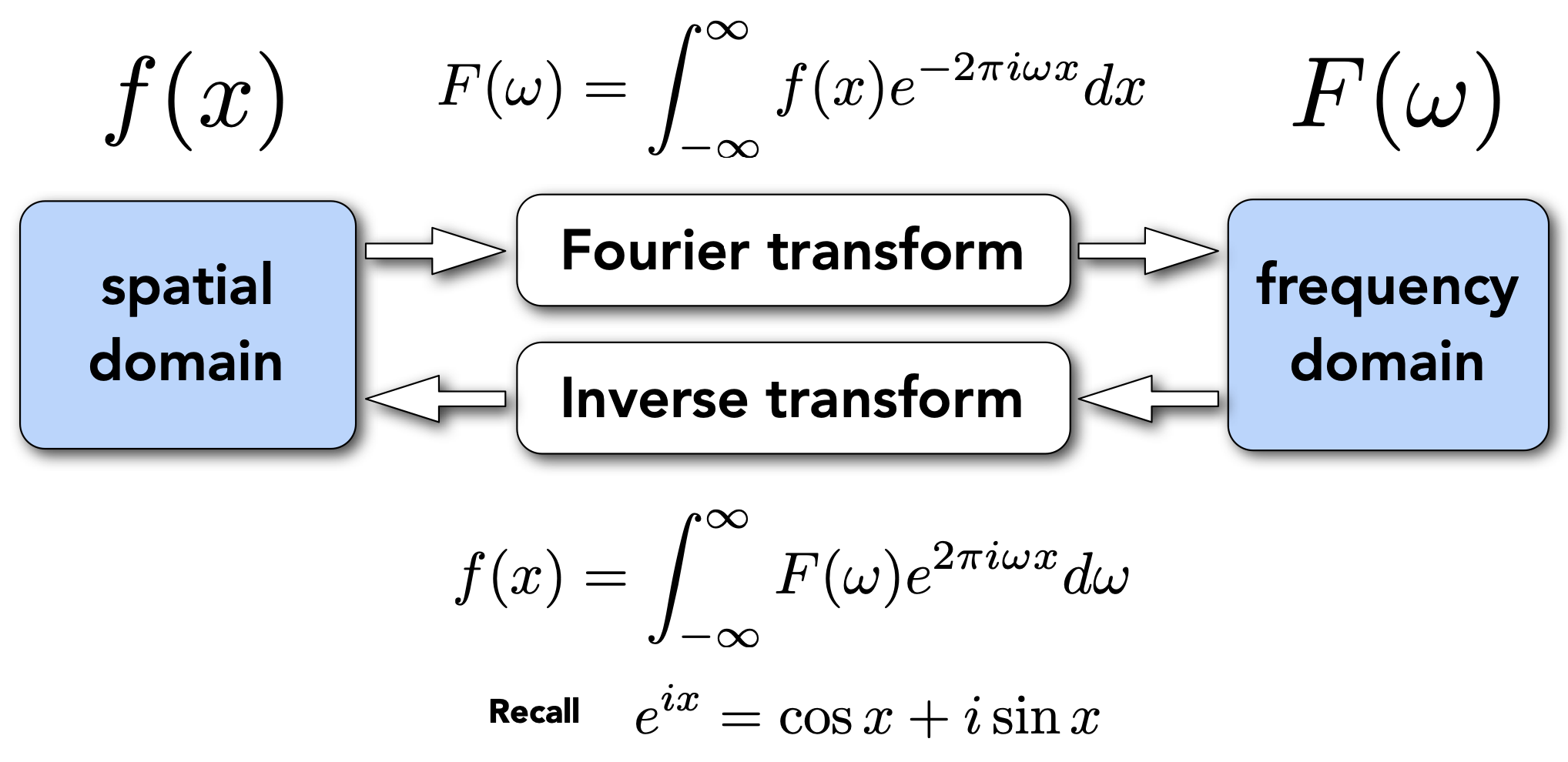
Frequency Domain 频域
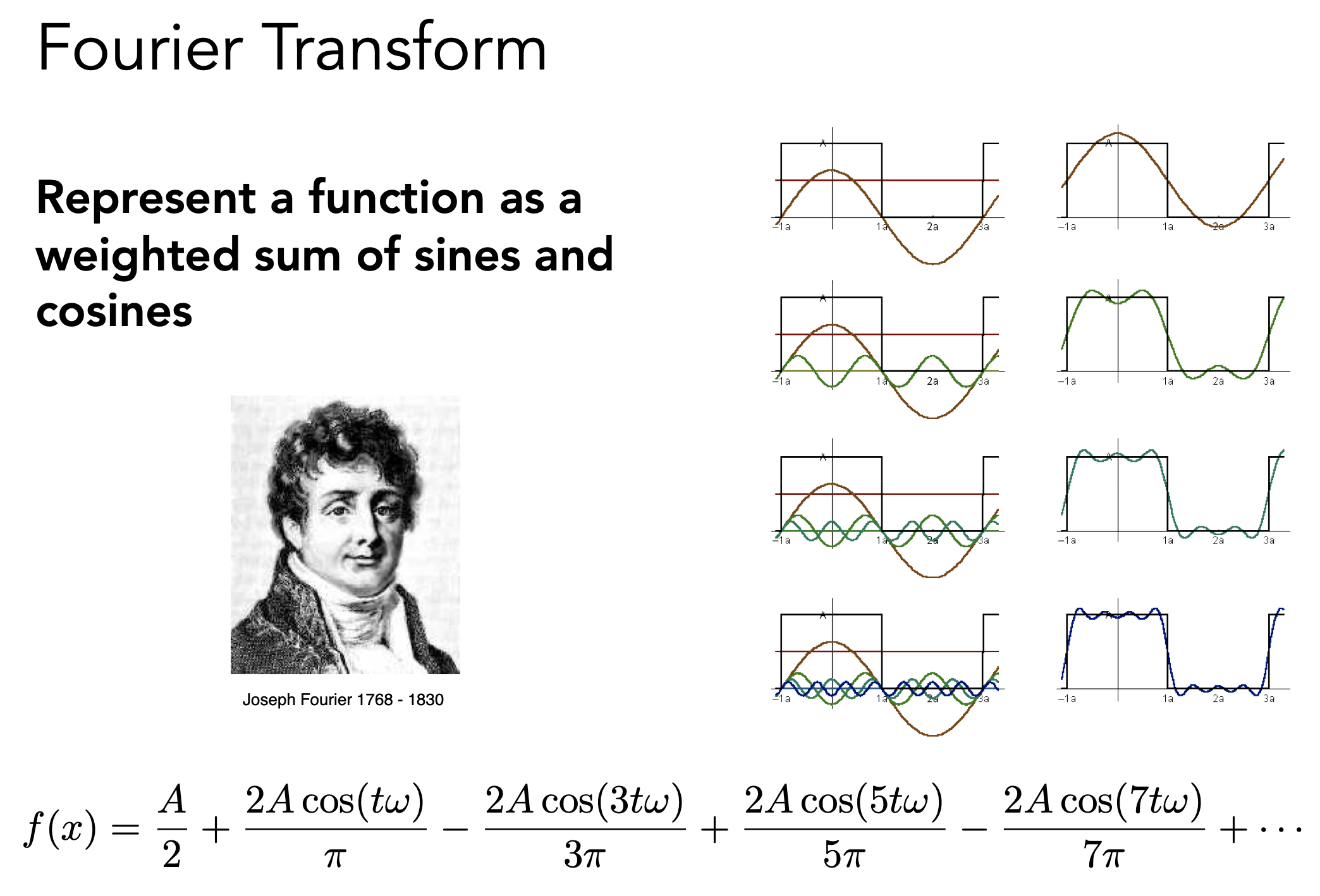
前置知识 - 信号处理
- 傅里叶级数展开:任何一个周期函数都可以写成一系列sin和cos的线性组合,和常数项
- 傅里叶变换和傅里叶级数展开
- 通过傅里叶展开可知,上述函数可展开成不同频率的函数
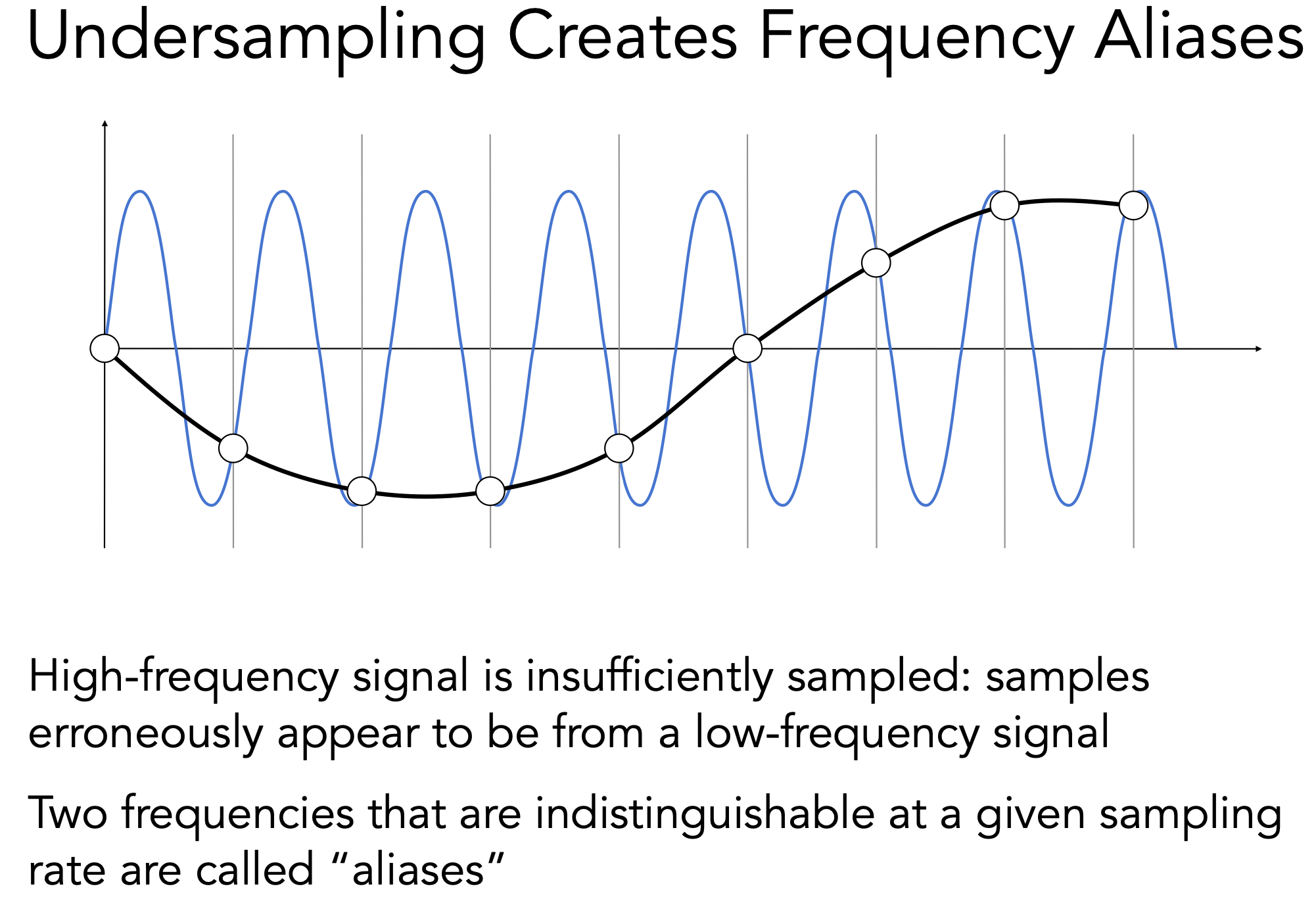
走样
- 对于傅里叶展开后的函数采样,高频部分出现走样
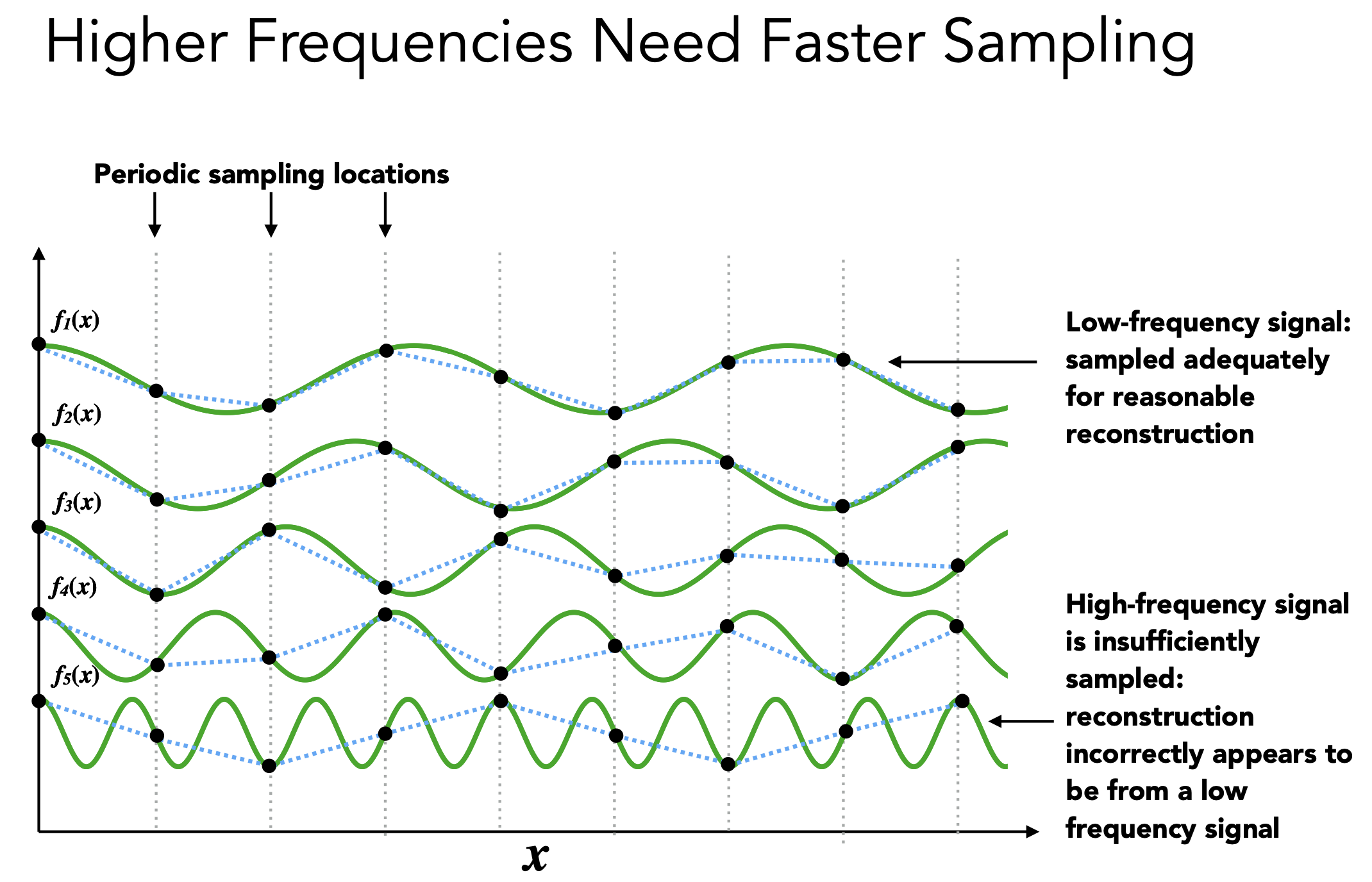
- 奈奎斯特采样定理:采样频率要大于信号最高频率的2倍,才能无失真的保留信号的完整信息
- 走样:同样的一种采样方法,采样两种不同频率的信号,得出的结果无法进行区分
- 对高频信号通过低频采样出现的走样
- 对高频信号通过低频采样出现的走样
Filtering 滤波
- 滤波:把某个特定频率抹去
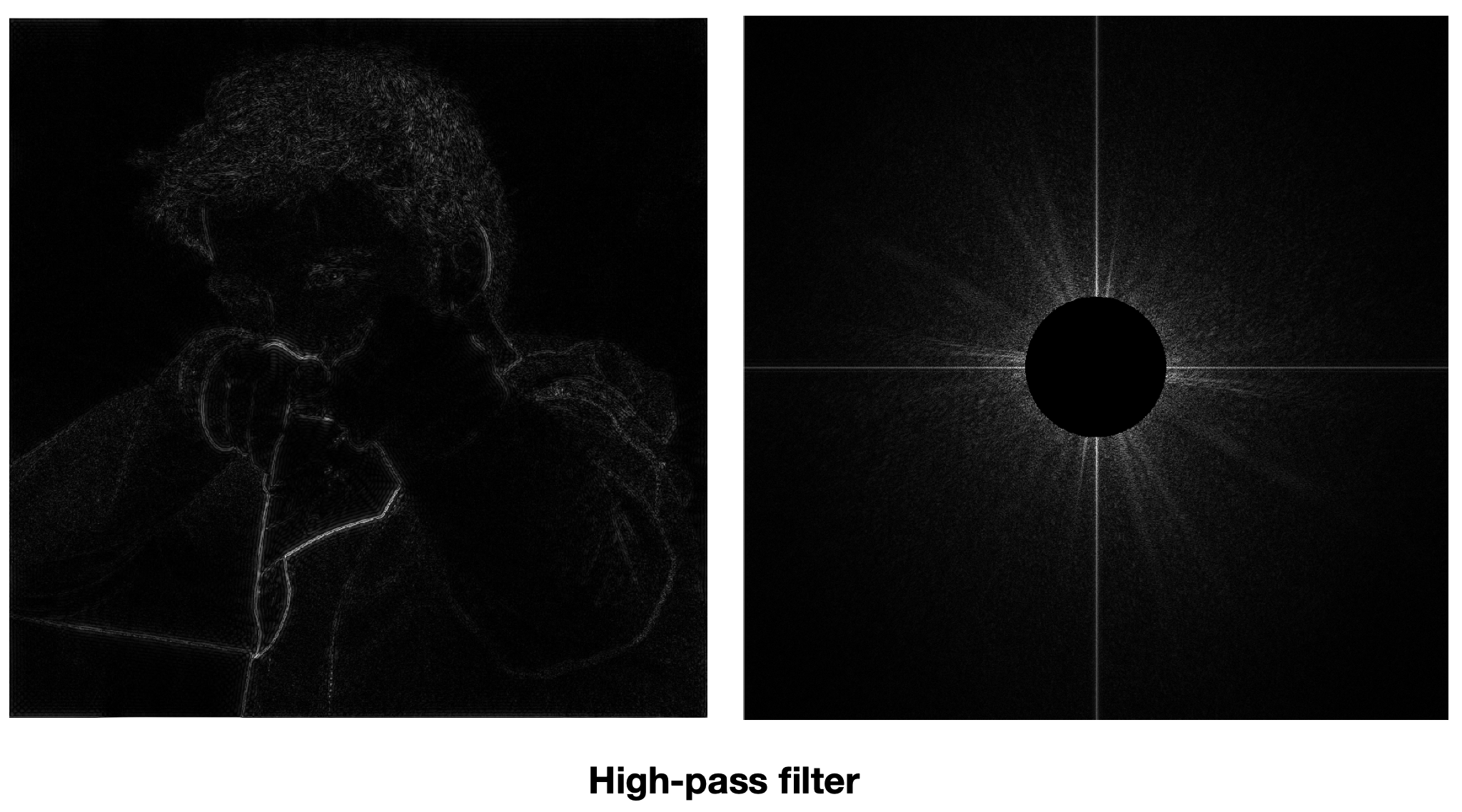
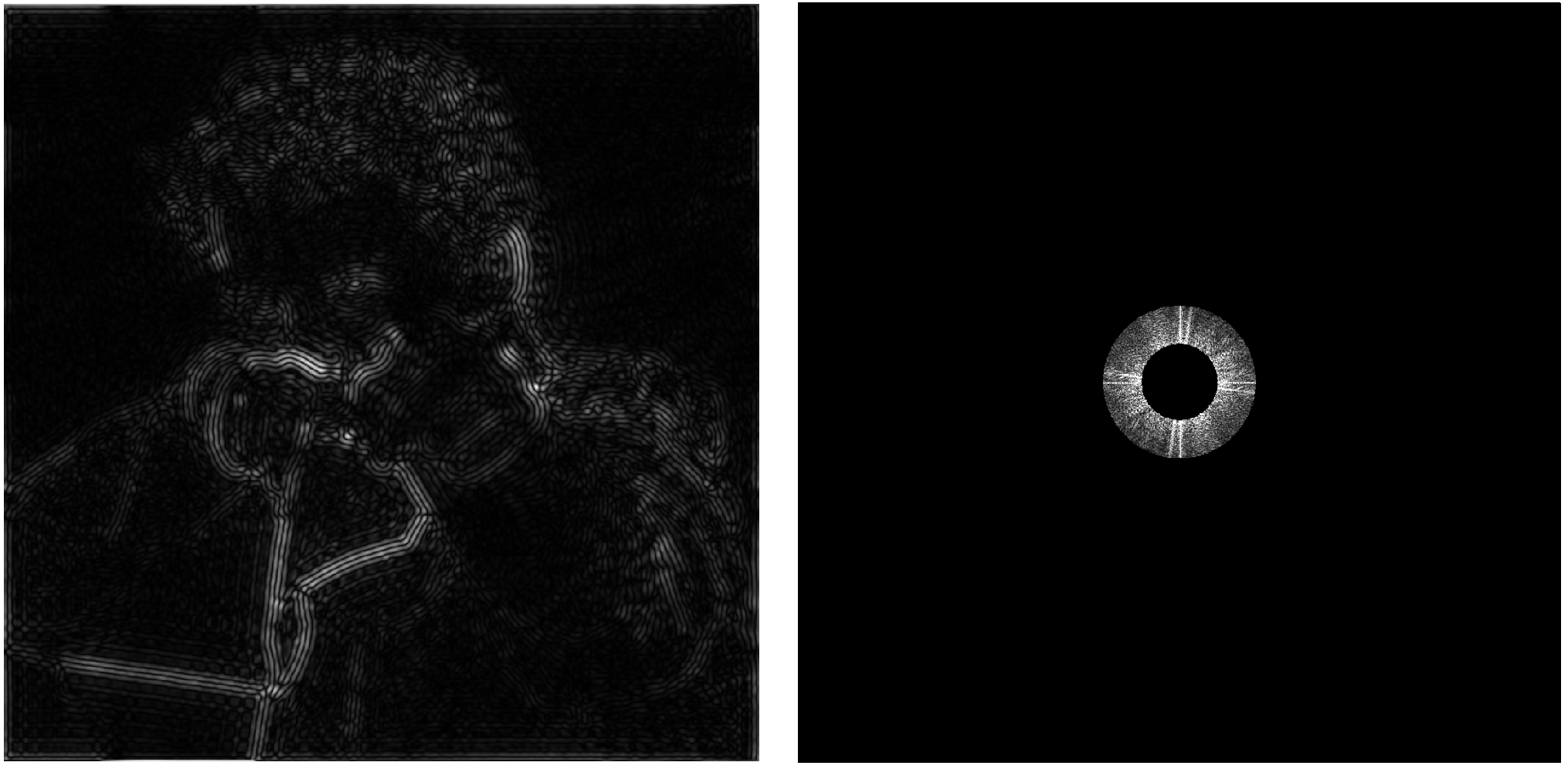
- 对图像进行傅里叶变换(变成频域空间

- 右图,中心为最低频。图像细节为高频信息
- 右图十字出现原因:图片在平面上平铺,左右边界和上下边界交界处信号变化剧烈,使得四个方向出现高频信号。
- 对图像进行高通滤波
- 对图像进行低糖滤波
中通滤波
滤波器和卷积效果相近,但原理不同
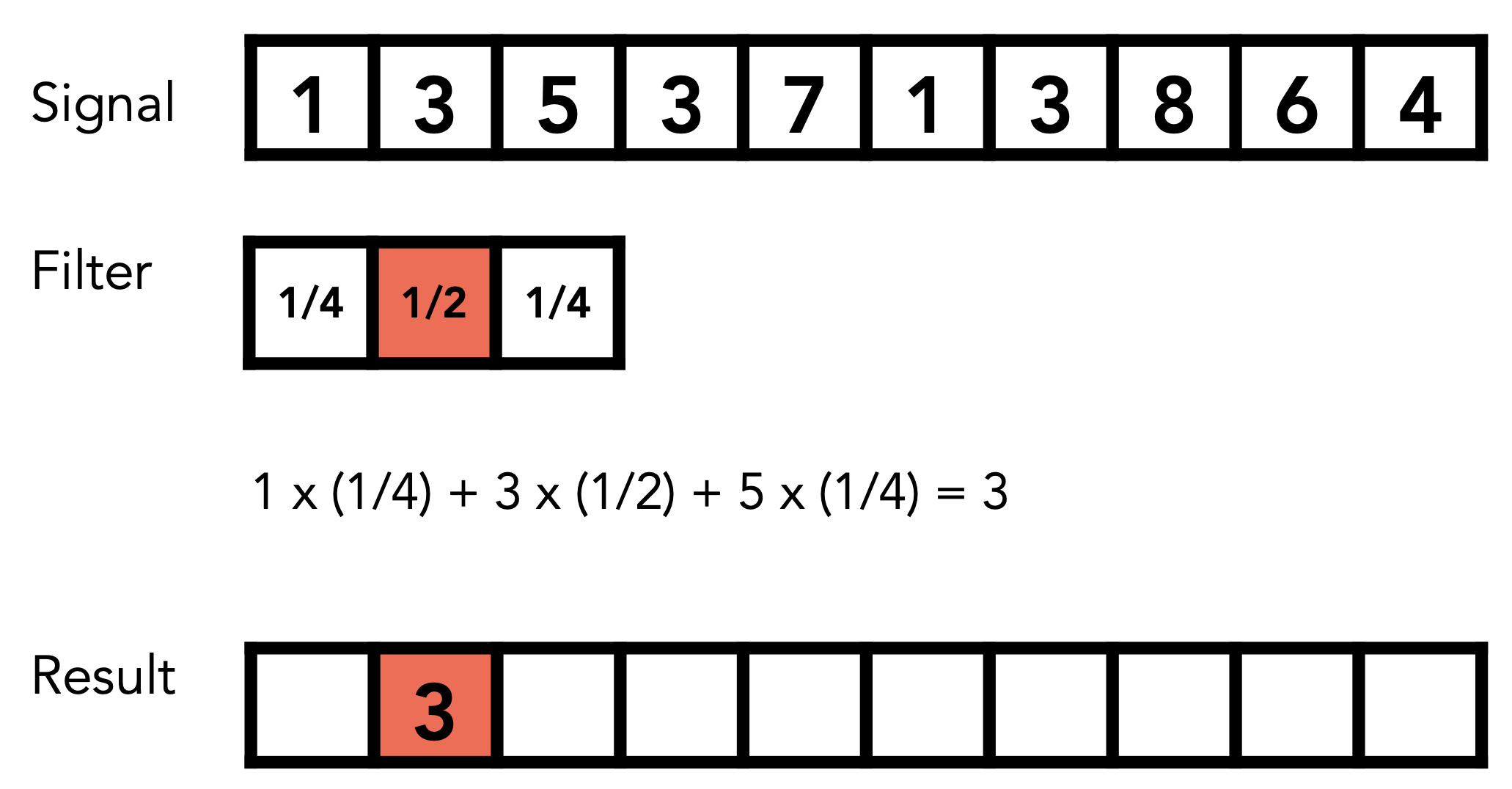
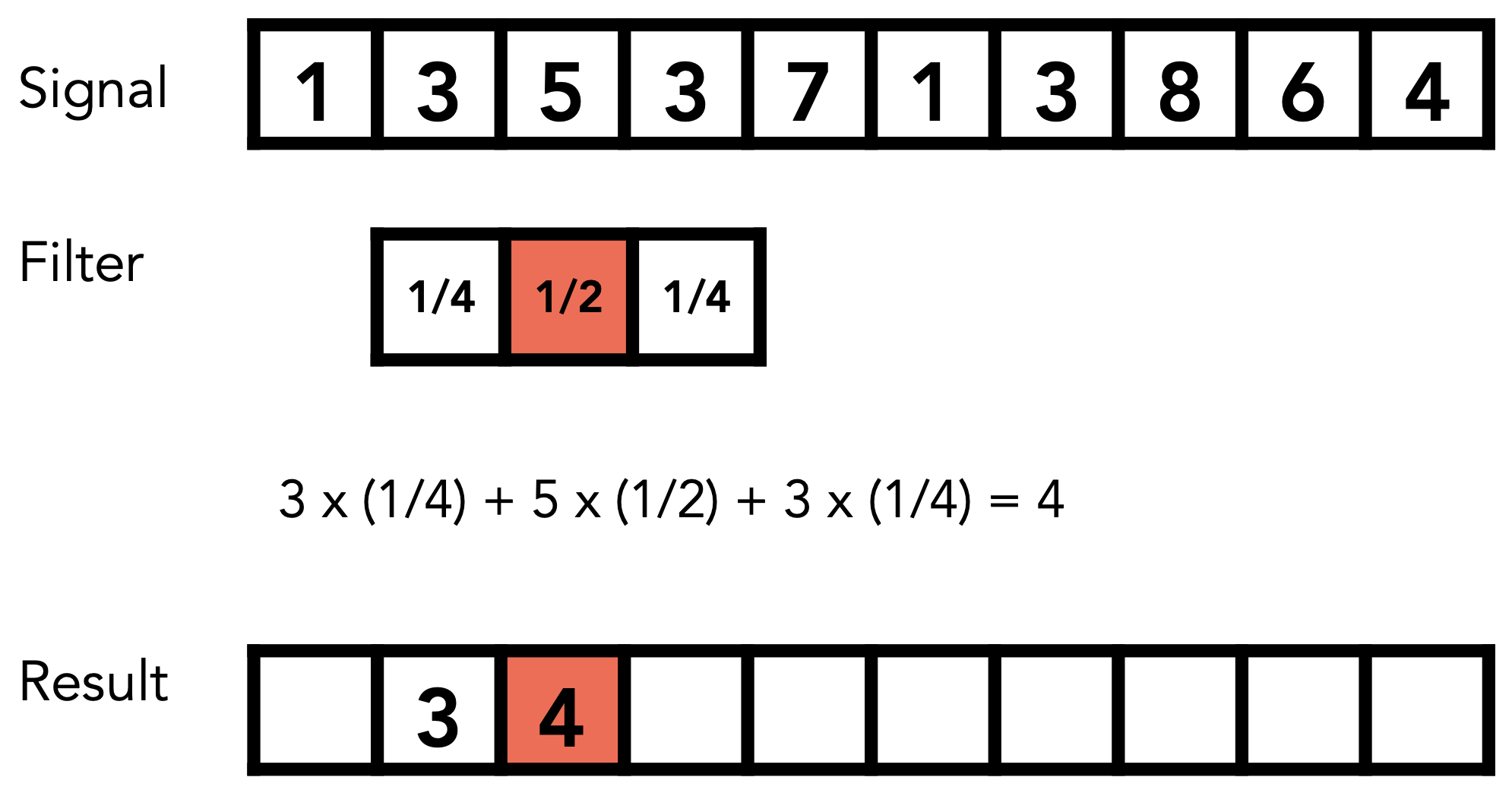
卷积补充:如何通俗易懂地理解卷积
- 卷积可帮助实现平滑算法

- 计算过程说明

- 计算过程模拟
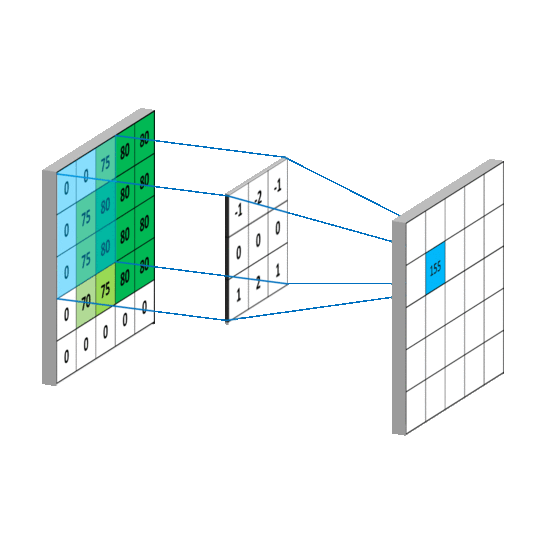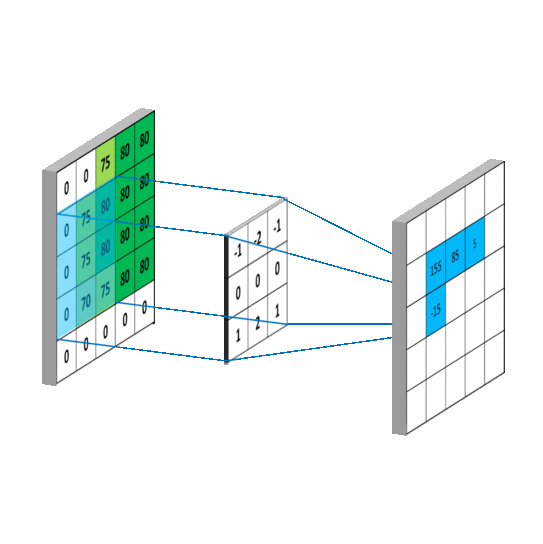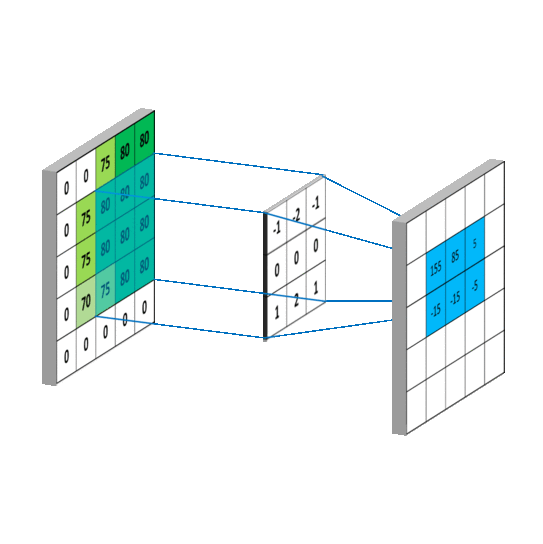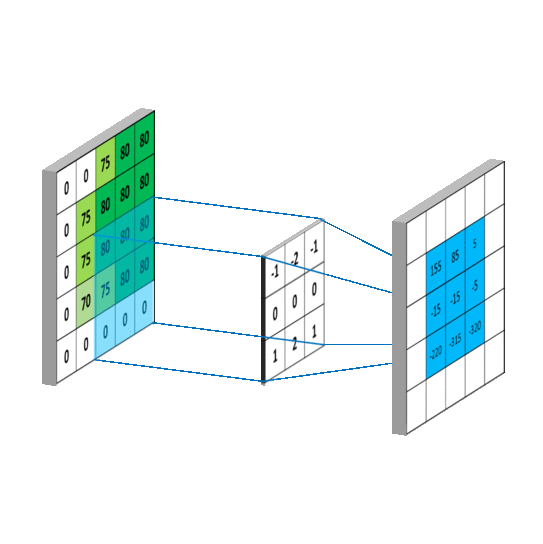
- 卷积可帮助实现平滑算法
- 图形学中Convolution:理解为加权平均
- 卷积定理:两个信号时域上的卷积,是这两个信号频域上的乘积;反之,时域上的乘积,也等于频域上的卷积
- 理解:时域和频域差一个傅里叶的叠加
对图像进行滤波(有两种方法
- Option1: 在空域使用卷积进行滤波
Option2
- 利用傅里叶变换将空域图片转到频域空间
- 图像在频域下,与卷积核相乘
- 通过逆傅里叶变换重新变回空域
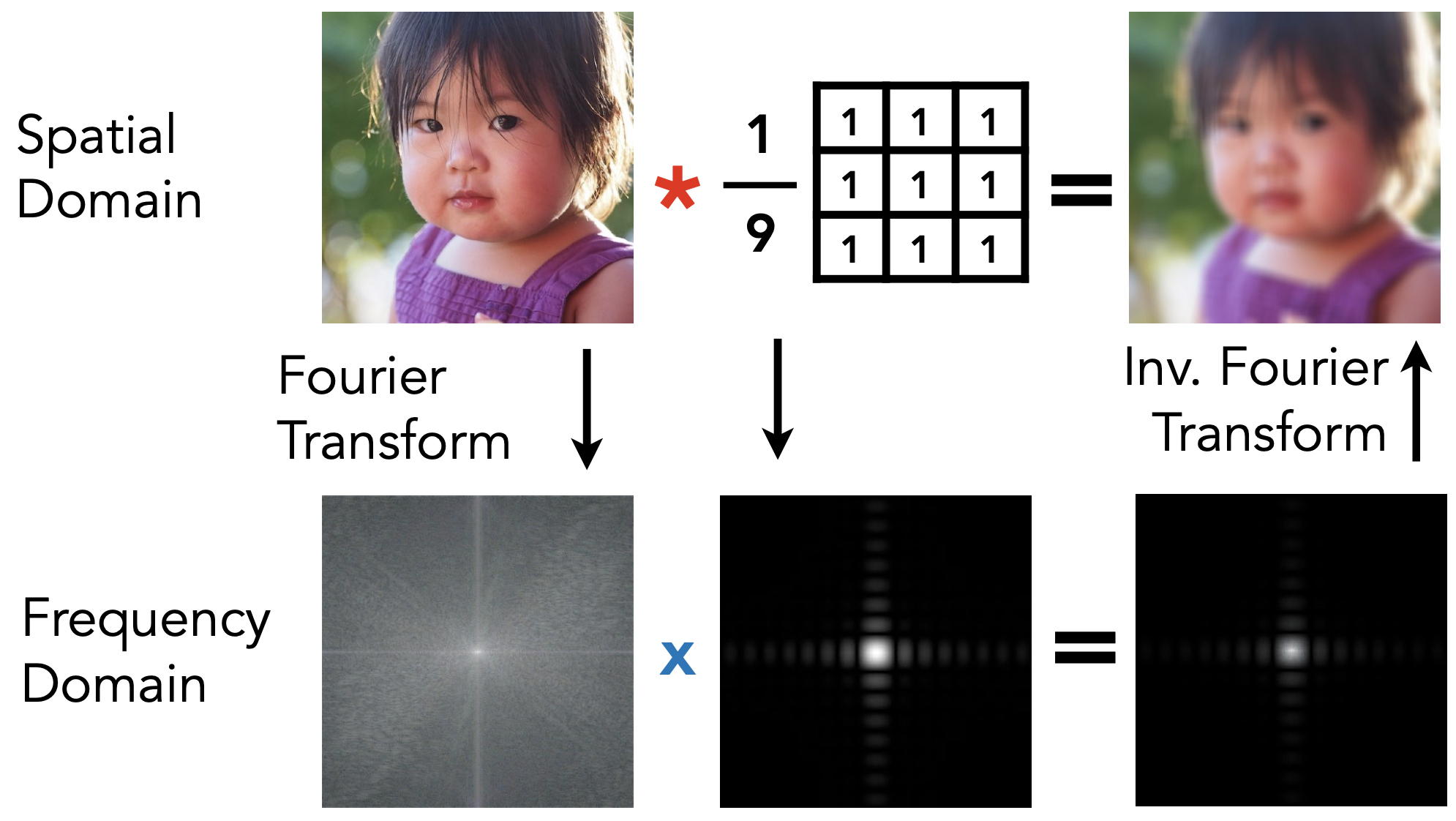
- 这个例子:一个像素* = 一个像素和周围一圈像素求平均
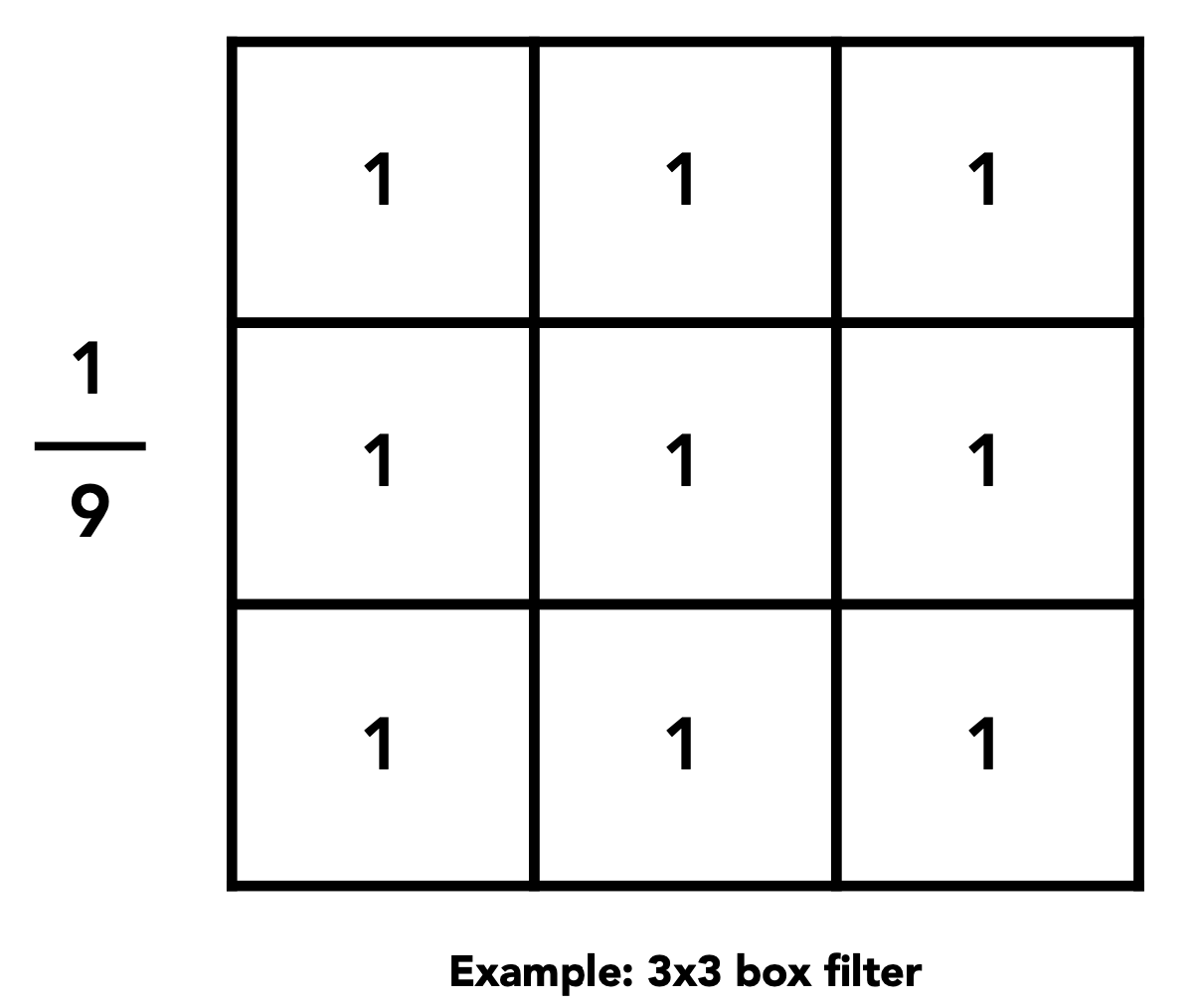
卷积核Box Filter
Box Function = 低通滤波
Wider Filter Kernel = 更低的频率

- 理解:利用更大的卷积核进行卷积操作,得到的卷积频率会更低
Sampling采样 = Repeating Frequency Contents
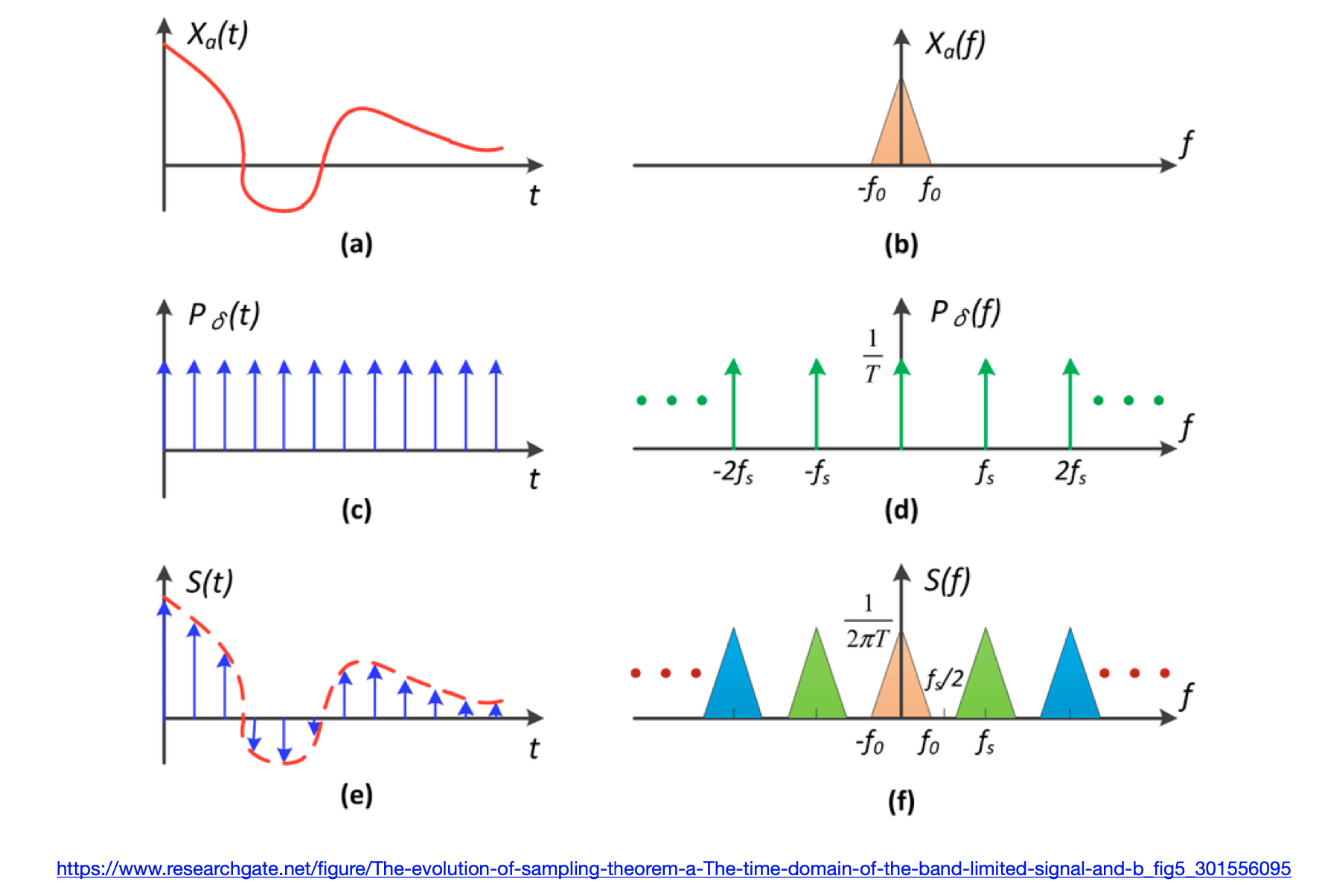
- 上图
- (e)是(a)和(c)在时域上的乘积
- (f)是(b)和(d)在频域上的卷积
- 通过观察(b)和(f),发现采样的过程是重复原始函数的频谱
- 走样 = 频谱上的混叠
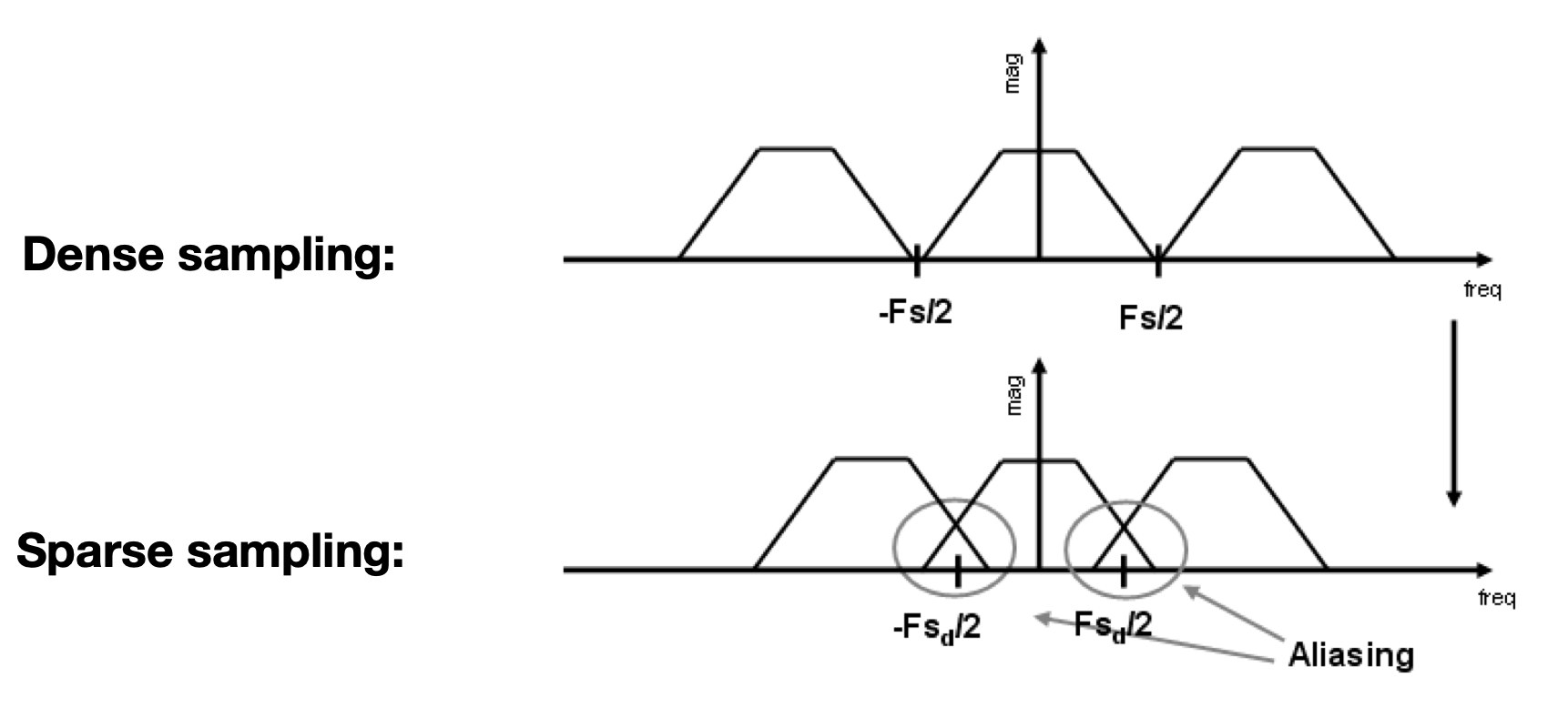
- 冲激函数周期变大等于冲击函数频域周期变小,则相乘后函数频域也变小,因此“粘贴的函数图像”变密
反走样 Antialiasing
反走样原理
- Reduce Aliasing Error
- Option1: 增加采样率
- 增大冲激信号在频域的间隔
- 更高分辨率的显示器
- 缺点:成本高&需要很高的很高的分辨率
- Option2: 进行反走样操作
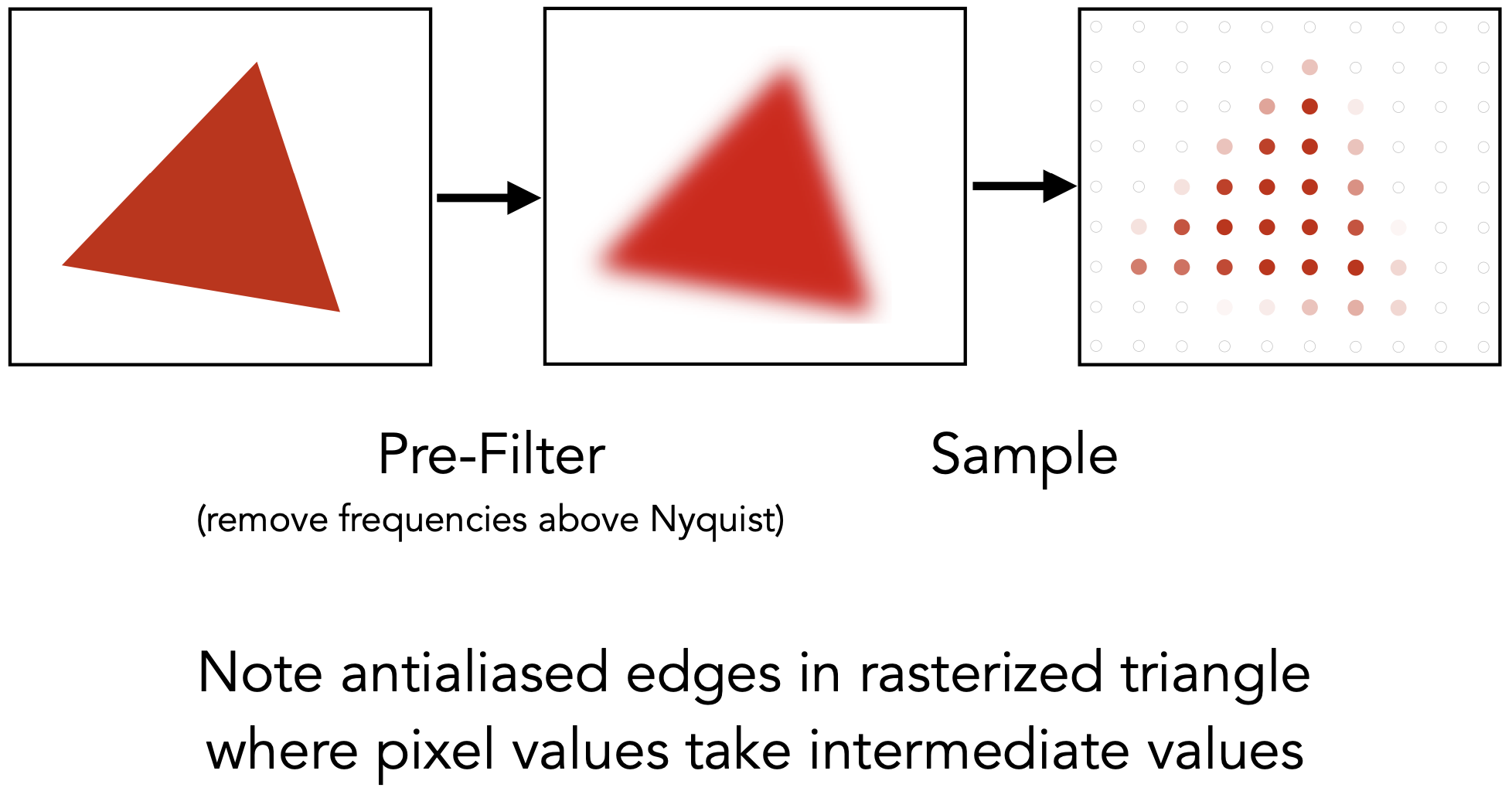
- 采样前,让信号在频域变窄 = 滤高频 = 图像模糊处理
- Option1: 增加采样率
- Antialiasing = Limiting, then repeating
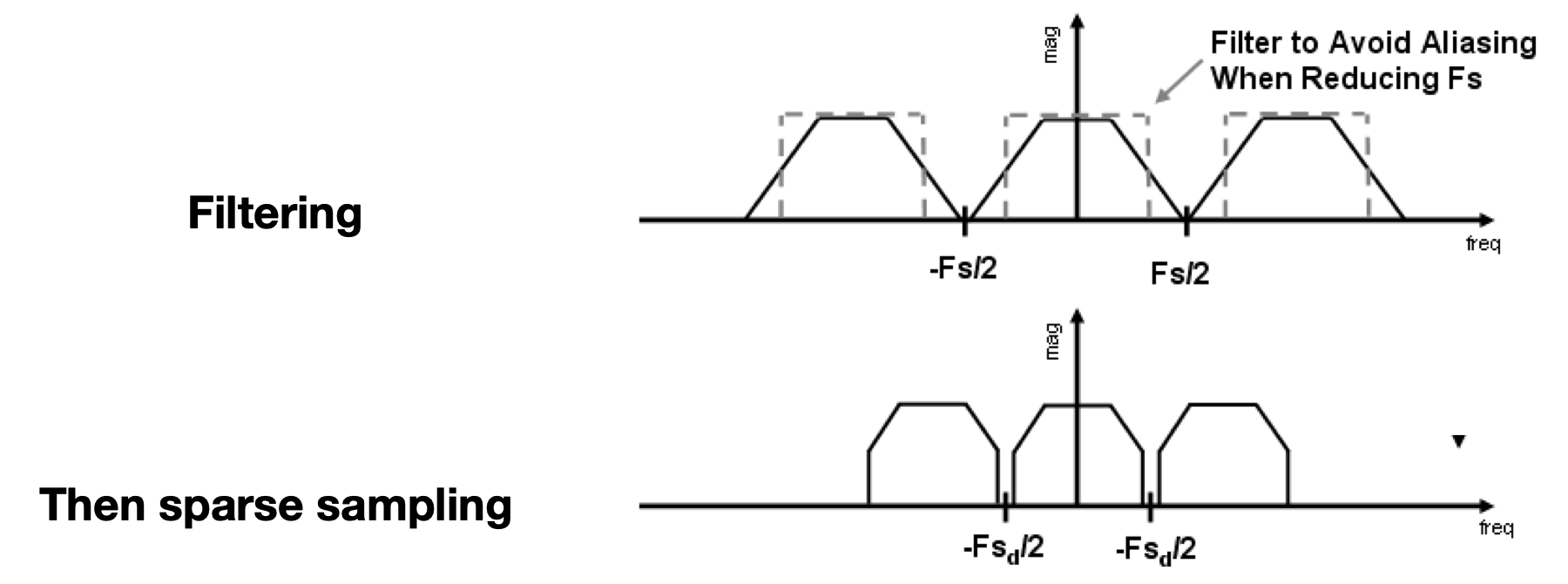
- 滤波后,避免上上图中的频域混叠
- 应用于图像处理中
- 一般采样
- 反走样——先对三角形模糊
- 一般采样
- 上述的滤波操作?(如何将三角形变模糊)
- 用一定大小的低通滤波器进行卷积
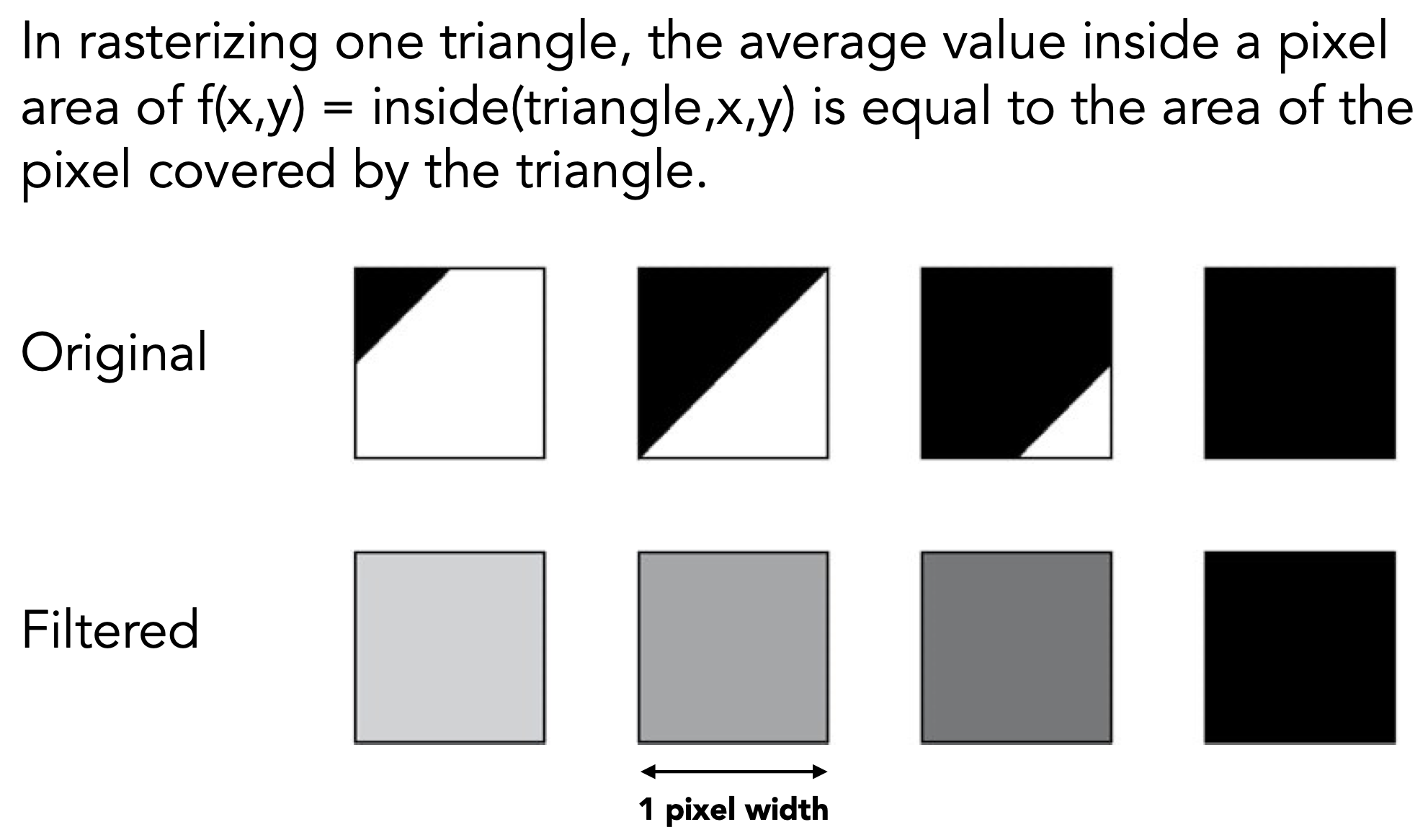
- 实际解决方法:对每个像素,把三角形求平均值,再采样

- 卷积:$f(x, y)$ by a 1-pixel box-blur
- Recall: convolving = filtering = averaging
- Then 采样,at every pixel’s center
- 卷积:$f(x, y)$ by a 1-pixel box-blur
- Antialiasing by Computing Average Pixel Value 通过计算像素平均值进行反走样
MSAA: Antialiasing By Supersampling
原理:超采样Supersampling
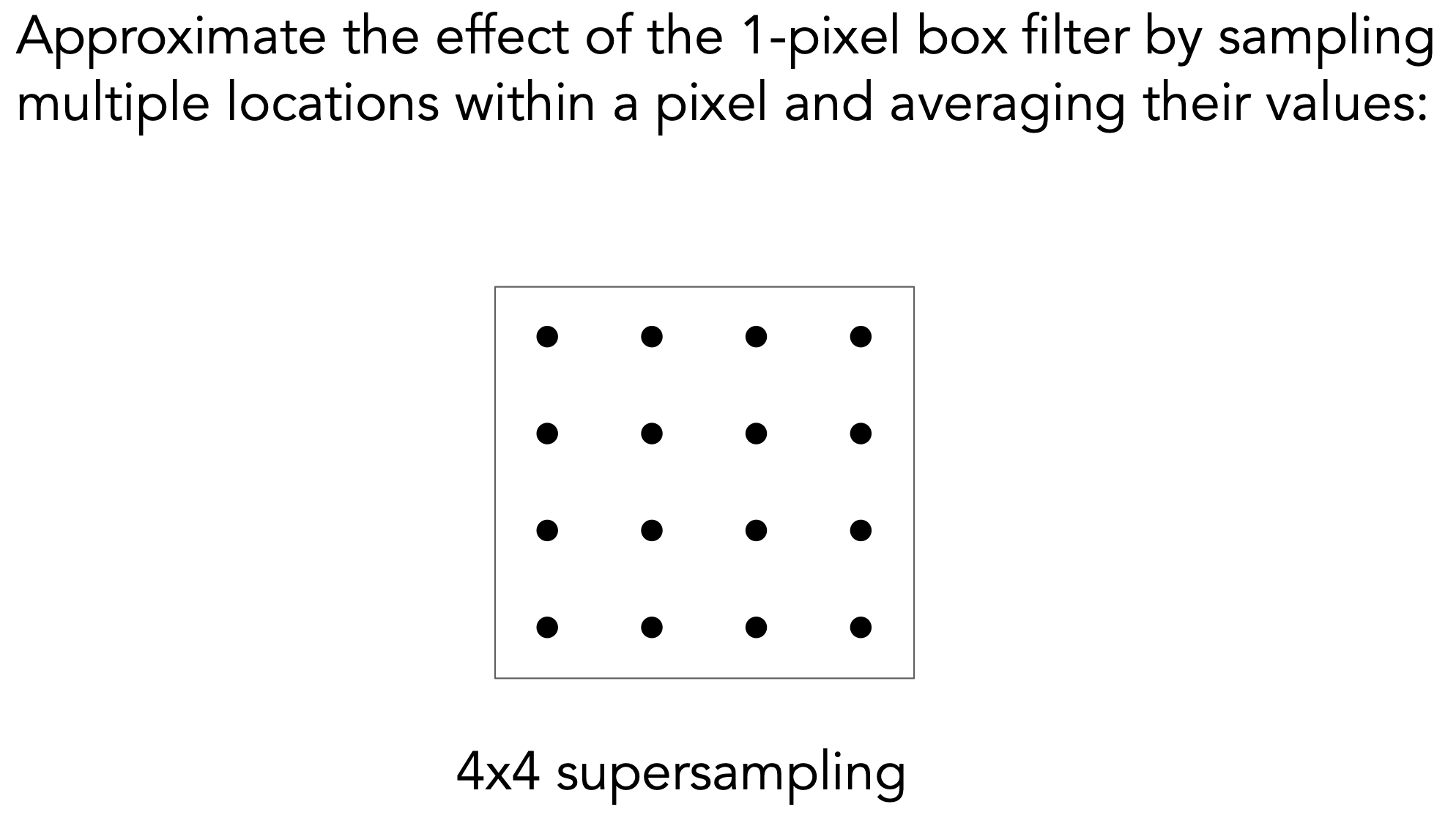
- 注意:MSAA实际上是对Blur的一种近似,是对信号的模糊,并没有提高分辨率(屏幕分辨率没改变)
- 过程举例
- 增加采样点,挨个判断是否在三角形内;四个采样点,覆盖率有$0\%, 25\%, 50\%,75\%,100\%$
- 增加采样点,挨个判断是否在三角形内;四个采样点,覆盖率有$0\%, 25\%, 50\%,75\%,100\%$
MSAA的性能代价:计算量增大
实际应用中以降低性能代价,像素不会被规则的划分为NxN,而是会用更加有效的划分方法,一些点还会被临近像素复用。
FXAA: Fast Approximate AA
- 与增加样本数无关,属于图像的后期处理。速度快
- 过程:得到有锯齿的图后,通过图像匹配的方法找到边界部分,将边界换成没有锯齿的边界
TAA: Temporal AA
- 理解:将MSAA对应样本,从空间分布改变为时间分布
补:Super Resolution超分辨率 / Super Sampling
将小图放大,并避免锯齿的产生(举例:waifu2x)
DLSS: Deep Learning Super Sampling
- 通过深度学习,对放大后缺失的细节进行猜测
Visible可见性 / Occlusion遮挡
画家算法
- 对三角面排序,从远到近画,overwrite in the framebuffer
- 会出现错误遮挡
Z-Buffer 深度缓存
- 对像素内深度进行排序
- Ideas:
- 存储当先像素最小的深度
- 在生成最终图像的同时,同步生成另一张深度图(深度缓存)

- frame buffer stores color values
- depth buffer (z-buffer) stores depth
- 注意:
- 视口变换中,相机放在原点,看向$-Z$方向
- 这里为了方便计算,Z-Buffer中规定$Z$均为正值。则$Z$越小表示越近,$Z$越大表示越远
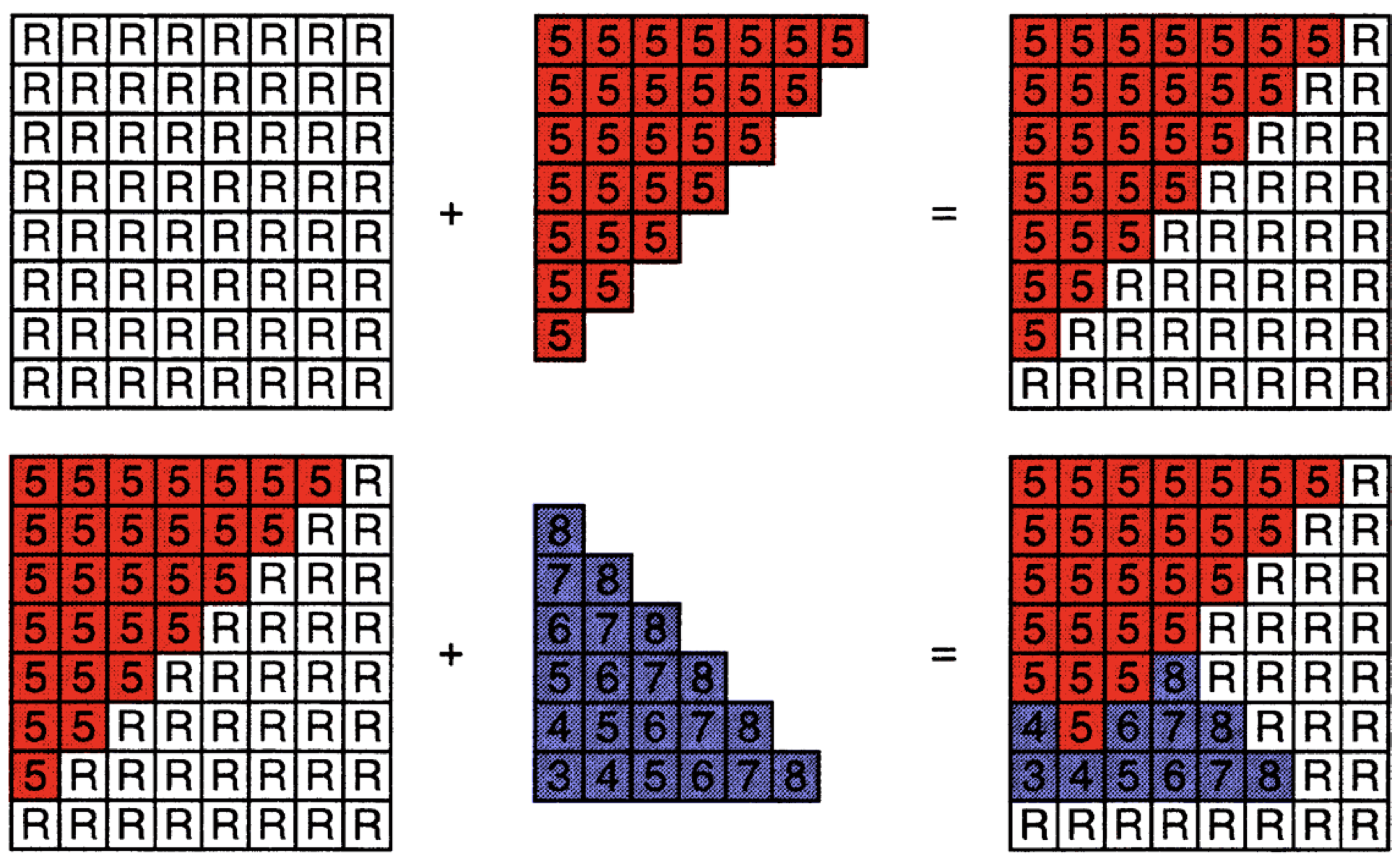
- 深度缓存实现步骤
- 初始化每个像素的深度缓存值都为$\infty$
- 对每个像素进行Rasterization:遍历每一个三角形中的每一个像素,若该三角形中该像素[x,y]的深度值z于zbuffer[x,y]中的值,则更新zbuffer[x,y]的值为z,并且更新该像素[x,y]的颜色
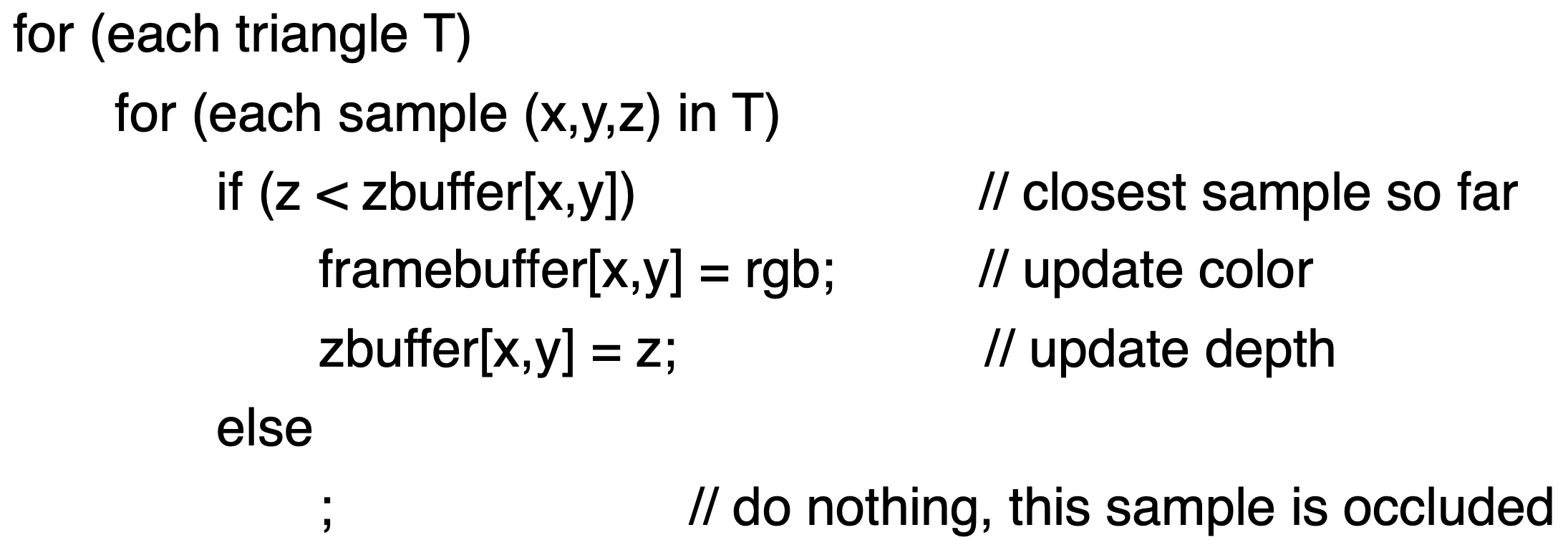
- 举例
- Z-Buffer复杂度
- 看完数据结构回来填坑

- 假设没有像素在同一深度(实际情况中,浮点数几乎不可能相等),深度缓存画三角形的顺序将不影响结果
- 若结合MSAA,则需针对每一个采样点进行相应的Z-Buffer深度操作
- Z-Buffer处理不了透明物体!
Shadows
Shadow mapping
(shadow mapping只能处理点光源的硬阴影)
Intro
- 一种图片空间的算法
- 计算阴影时,无需知道场景几何信息
- 需解决走样问题
- Key idea:若点不在阴影里,则摄影机和光源都可看到该点(若在阴影中,摄影机可看到但光源看不到)
Steps
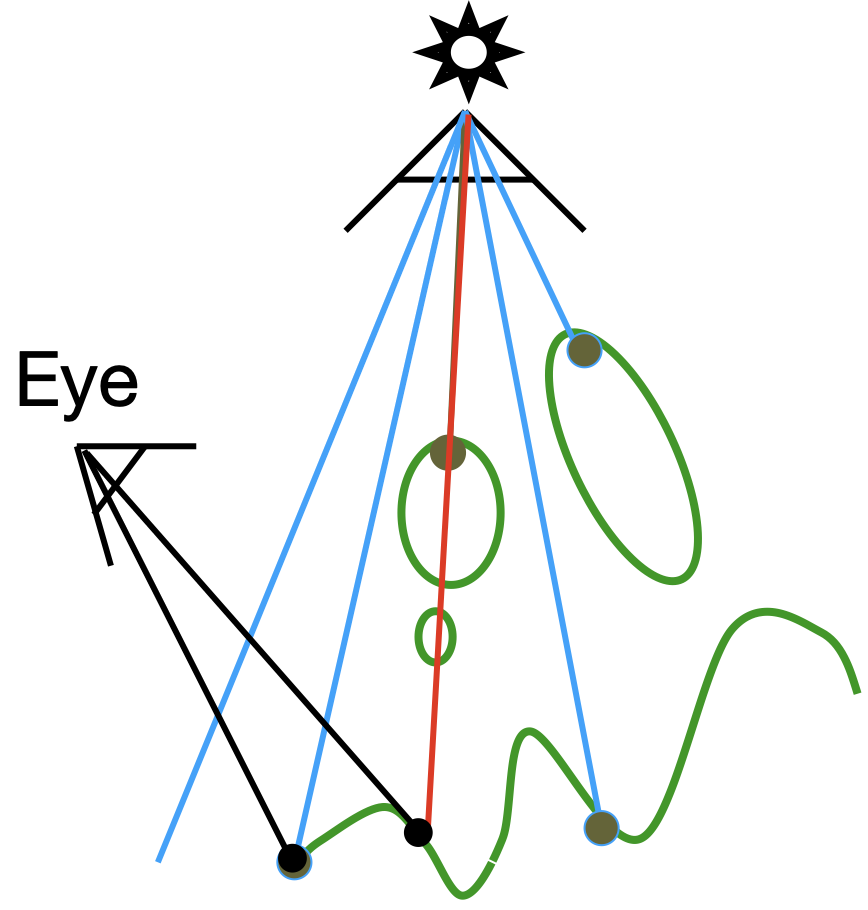
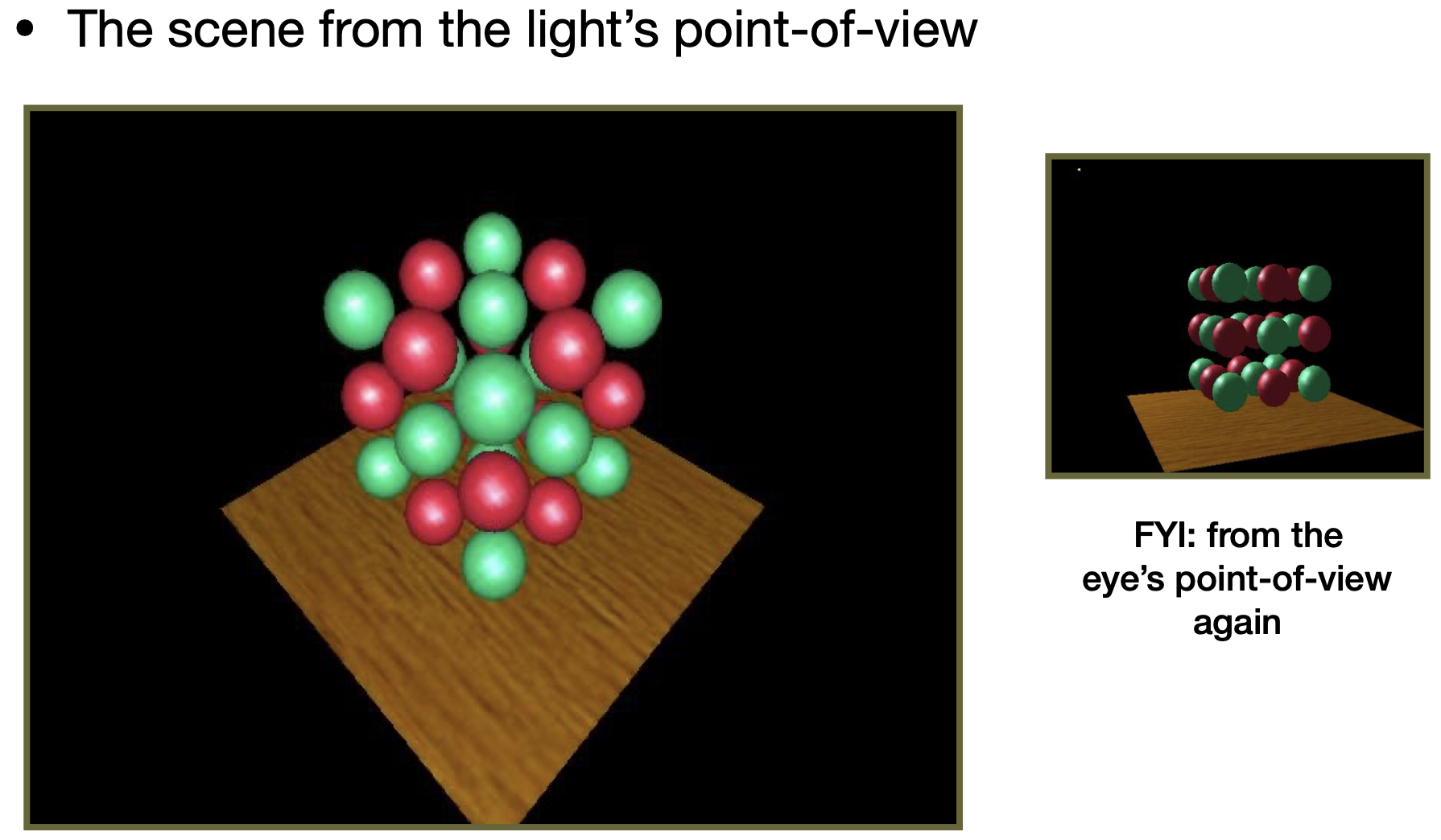
Render from light:从光源看向场景,记录深度图
Render from eye:从眼睛(摄像机)处看向光源,记录深度和颜色信息图
- Project to light:将眼睛所看见的点映射回光源所看到的深度图中对应的像素,计算该点在光源处看的深度,比较所得深度和第一步该点处深度。一致,则光源可以看到,该点不在阴影中;不一致,则光源看不到,该点在阴影中。
- 举例
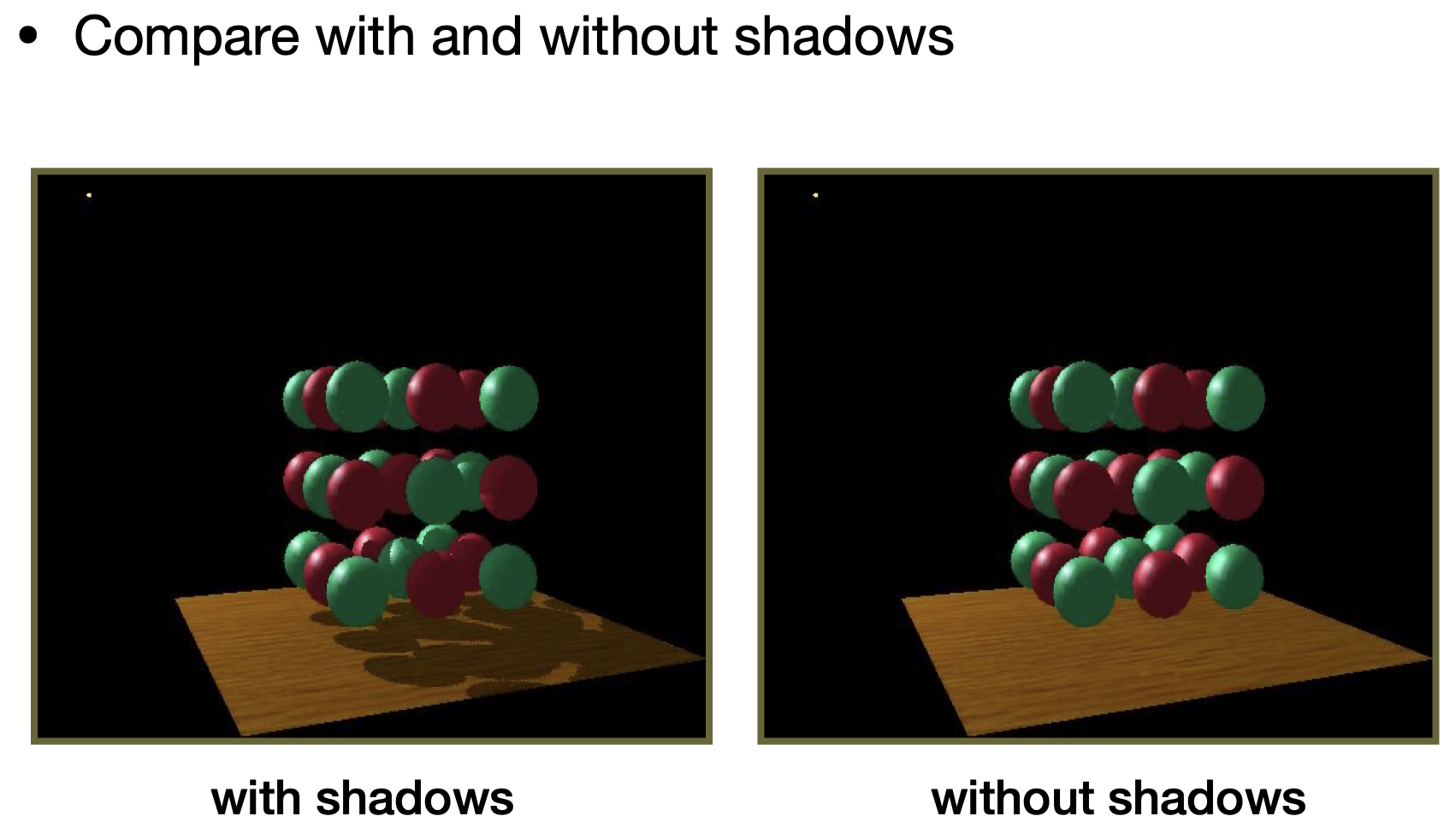
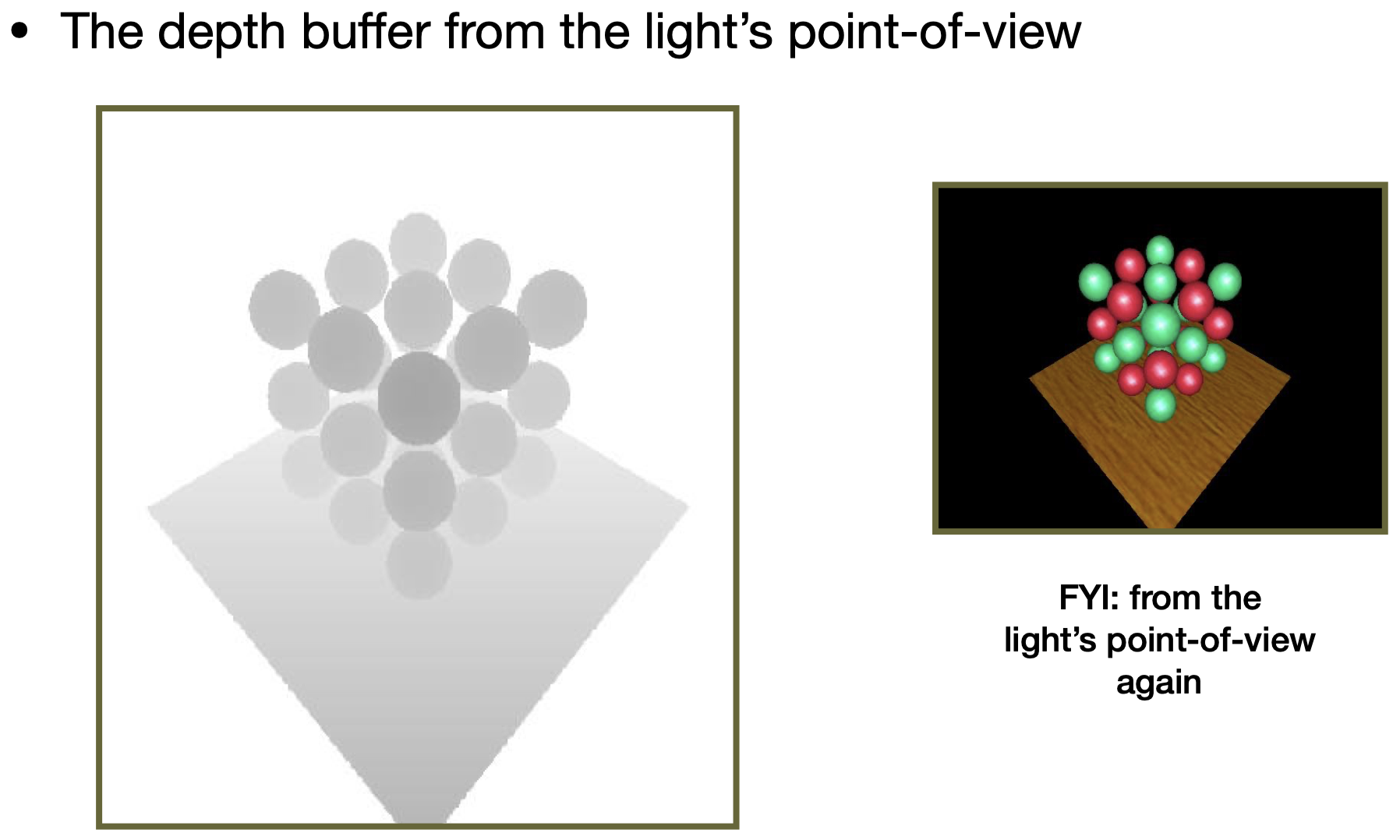

- 问题:边缘不清晰——浮点数很难判断相等,边界处深度判断易出错;shadow map分辨率会引起相应采样问题
Problems with shadow maps
- Hard shadows (point lights only)
- 补:软阴影
- 光源有大小才可能出现软阴影
- 出现在Penumbra半影区。本质是本影、半影、影子外的过渡
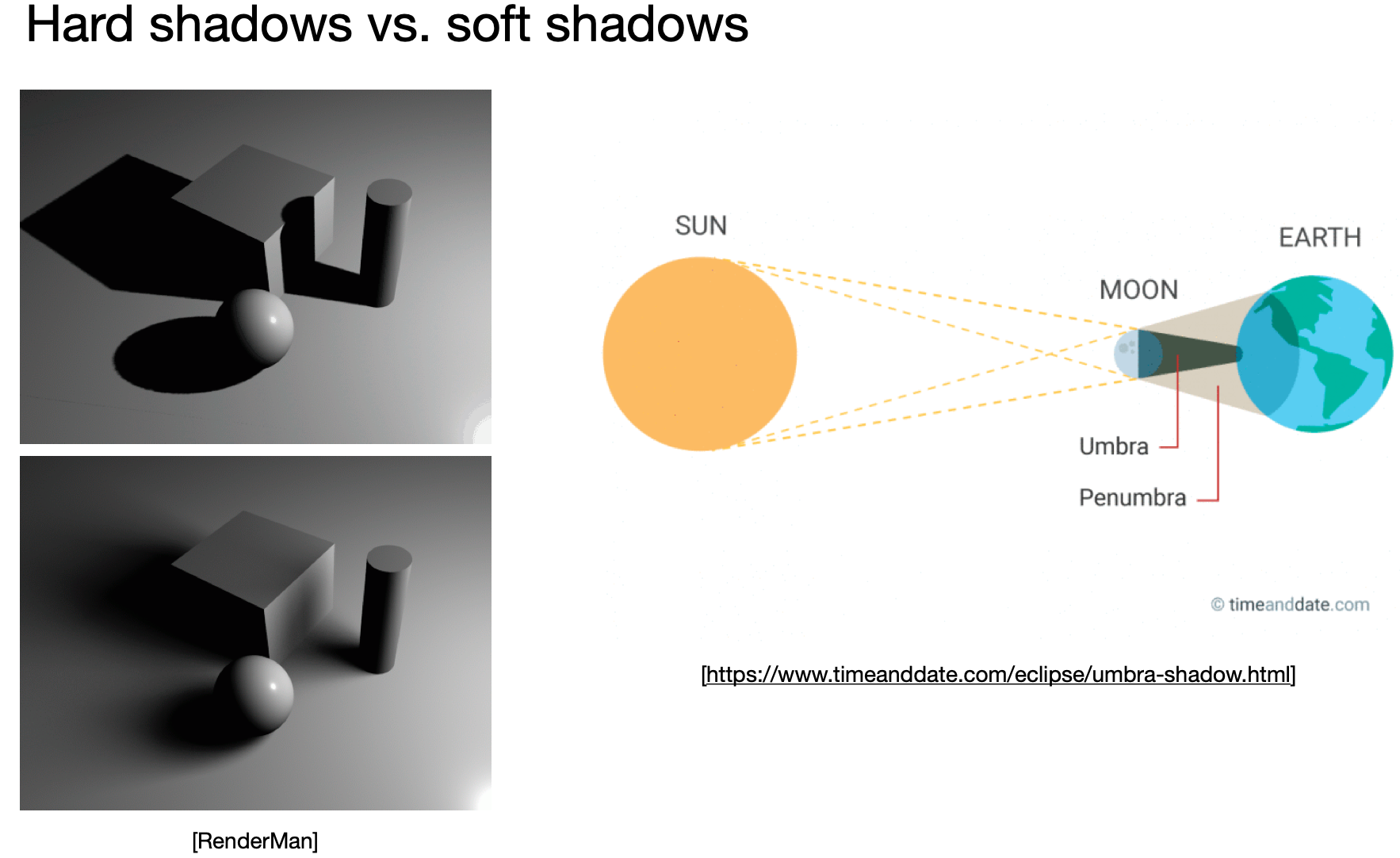
- 补:软阴影
- 阴影质量取决于shadow map分辨率(采样率低有锯齿,采样率高耗性能)(general problem with image-based techniques……)
- 涉及浮点深度值的相等比较,是指尺度、偏差、公差等问题