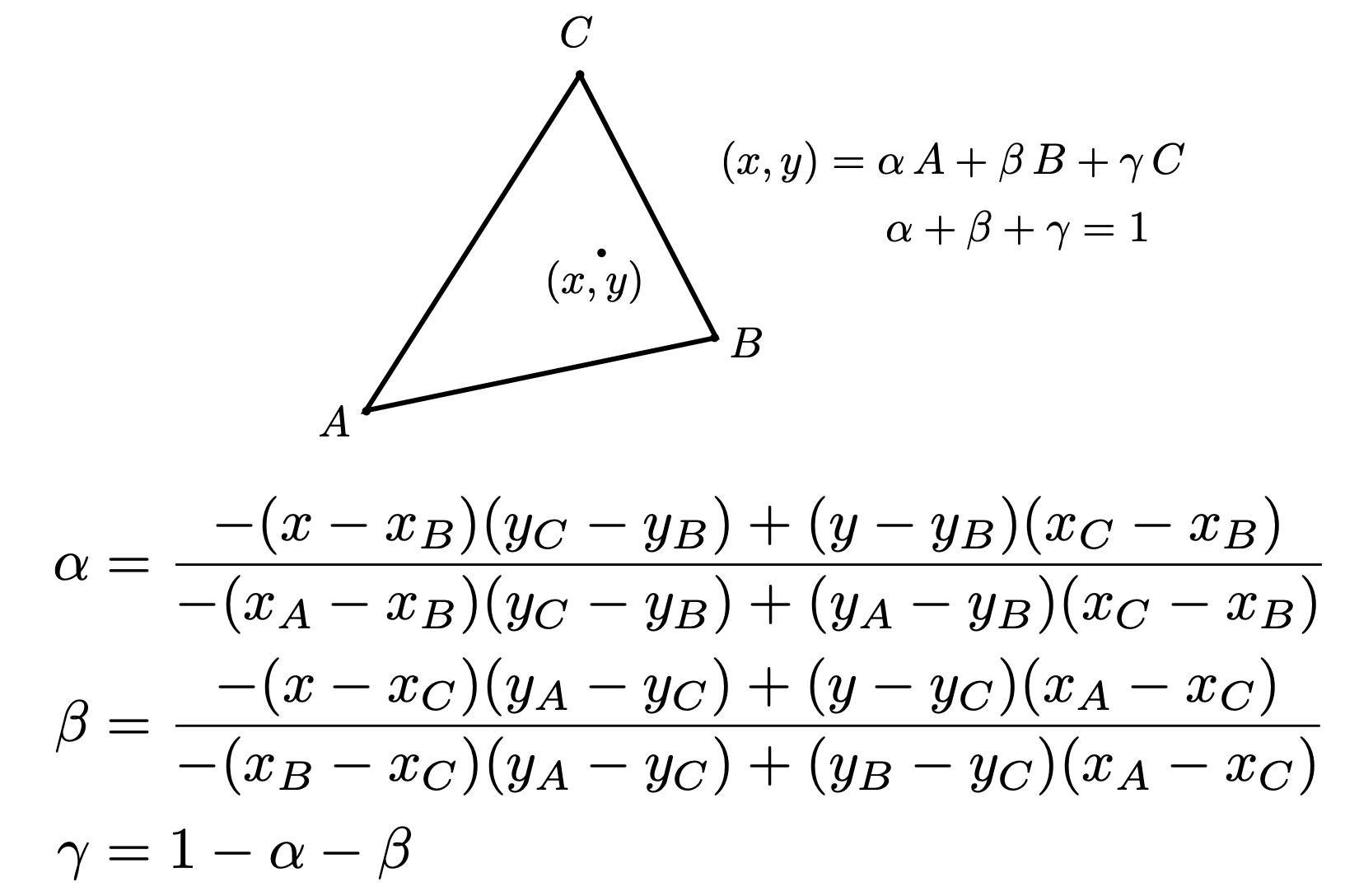Games101-P7-9 Shading

Posted on 2023-04-02 Edited on 2023-07-30 In Games101 Word count in article: 6.4k

P7 Preview
- Blinn - Phong Diffuse Reflection Model
  - Diffuse：
P8 Preview
- Blinn - Phong Diffuse Reflection Model：
  - Specular：
  - Ambient：
- Shading Frequencies
- Graphics Pipeline
P9 Preview
- Barycentric coordinate 重心插值：
- Texture Magnification
  - Bilinear Interpolation 双线性插值：
- Texture antialiasing (MIPMAP)
- Application of texture

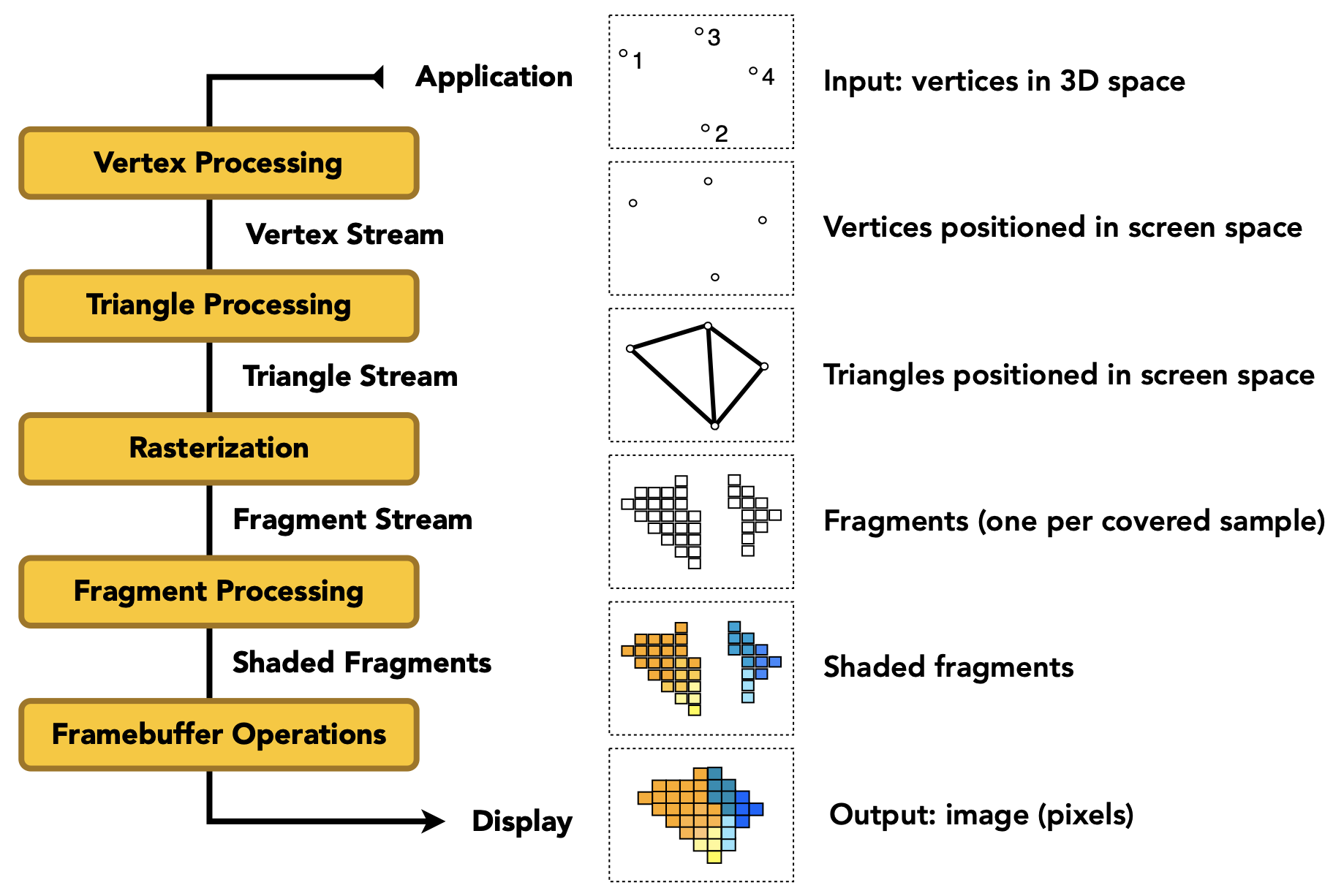
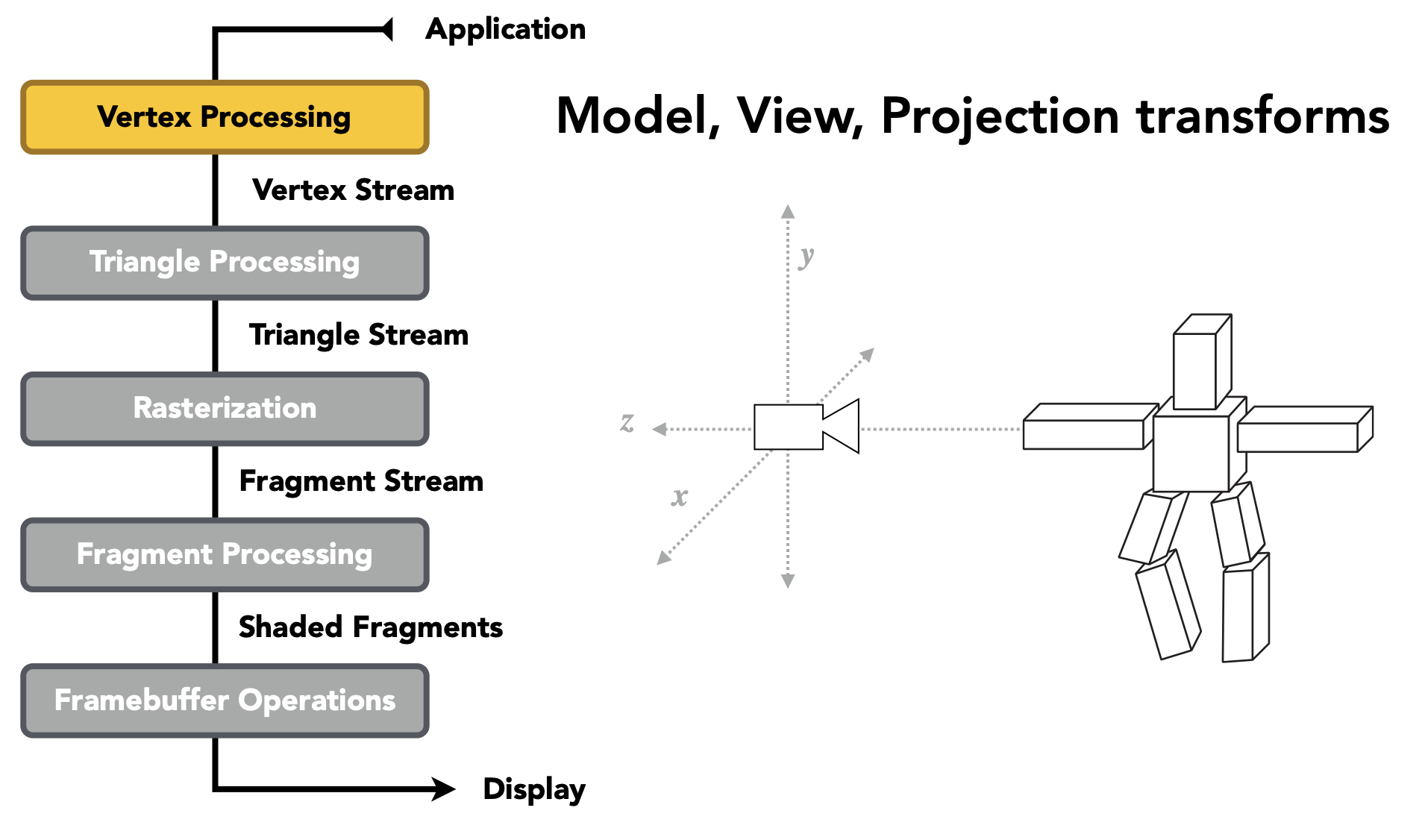
P7 Shading (Illumination, Shading and Graphics Pipeline)

回顾：Model - View - Projection - Viewport - Rasterization

Shading Definition

字典中：The darkening or coloring of an illustration or diagram with parallel lines or a block of color.
本课中：The process of applying a material to an object. // 不同材质和光线相互作用的方法不同

简单的着色例子：Blinn - Phong Reflection Model

Blinn - Phong Reflection Model是经验型模型，并不完全符合物理

Shading in Local

光——得出反射模型
- Specular Highlight 高光
- Diffuse Reflection 漫反射光
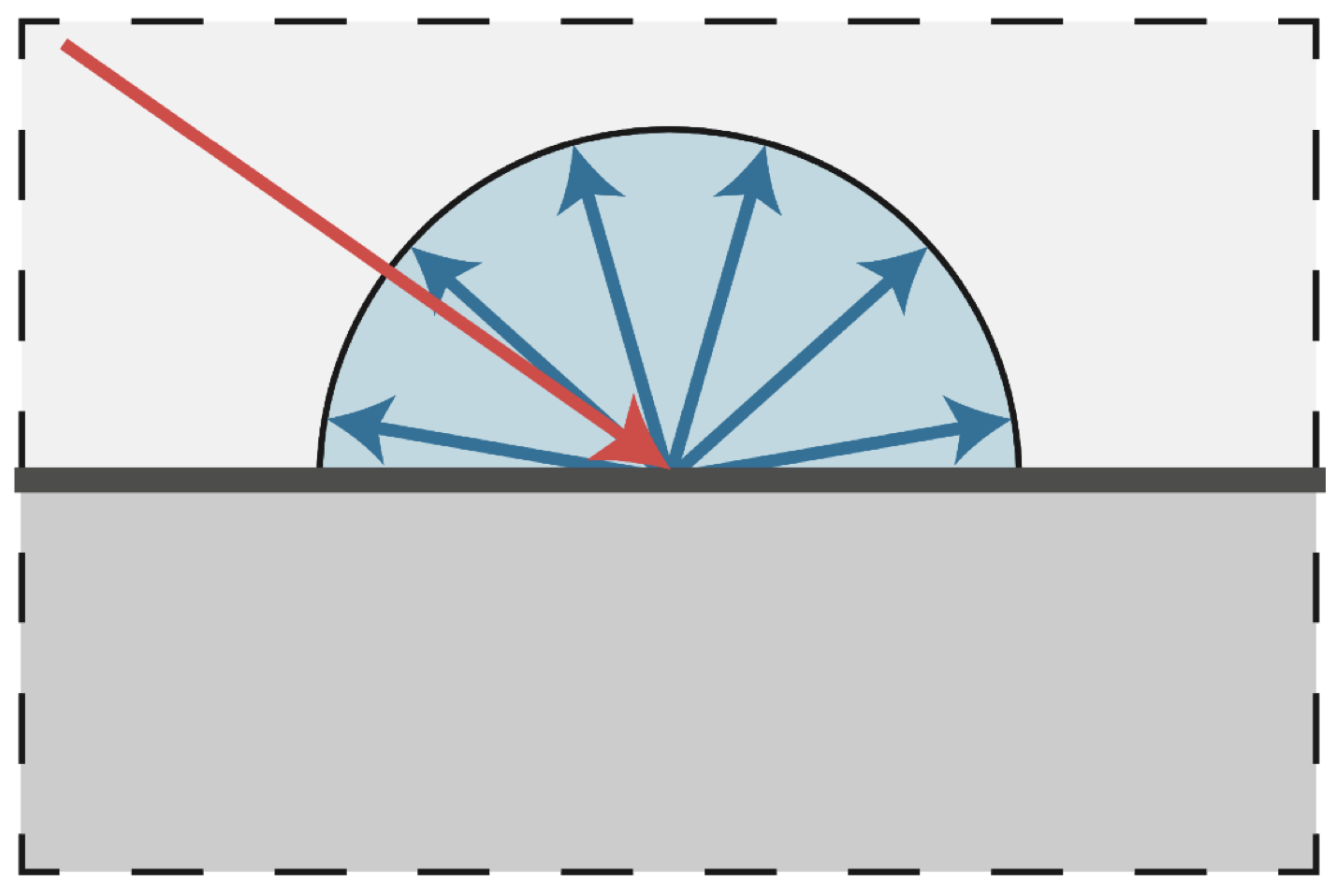
- Ambient Light 环境光：不是直接接收到的光照，是通过物体反射接收到的光照
Shading Point：相机所观察到的点
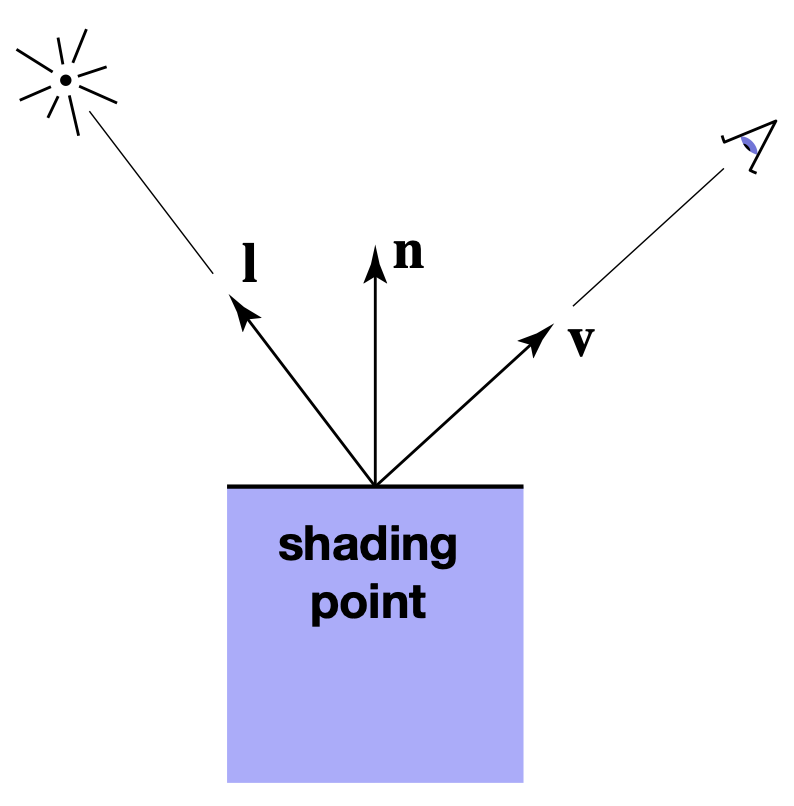
- input：（一下所有向量只表示方向，均为单位向量，由两点向量归一化得到）
  - Viewer direction, v：观测方向，shading point向相机连线的方向
  - Surface normal, n：法线方向
  - Light direction, l：光照方向，shading point向光源连线的方向
  - Surface Parameter(color, shininess, …)：表面属性
注意⚠️：Shading in Local只关注该点自身着色，产生明暗变化，不产生阴影，与shadow无关

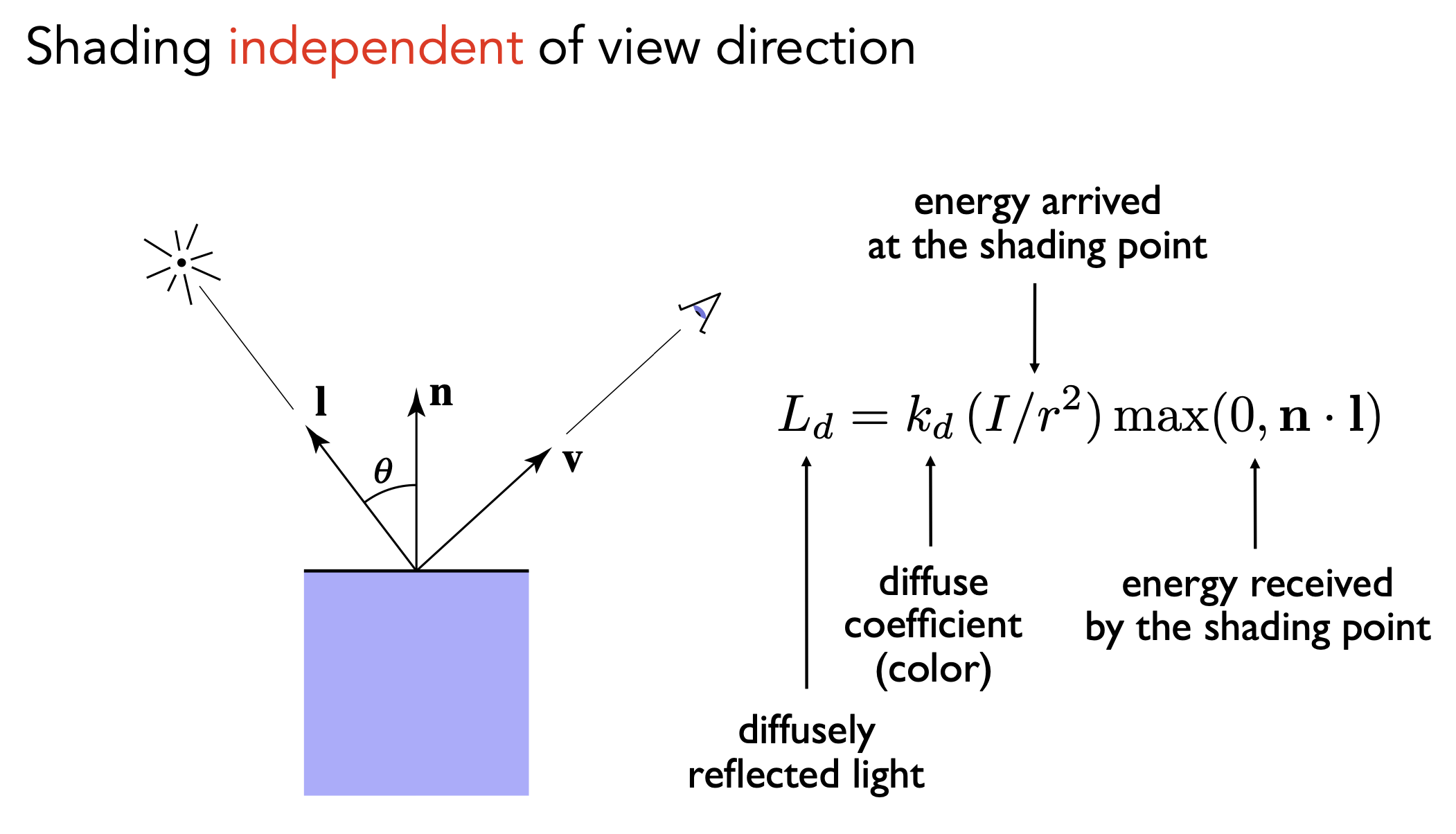
Diffuse Reflection 漫反射

漫反射
为什么光以不同的角度照射到物体表面，得到的明暗不同
- Lambert’s cosine law（Lambert余弦定理）：物体表面单位面积接收到的光照和$cos\theta(=n \cdot l)$成正比，直射接收到所有能量
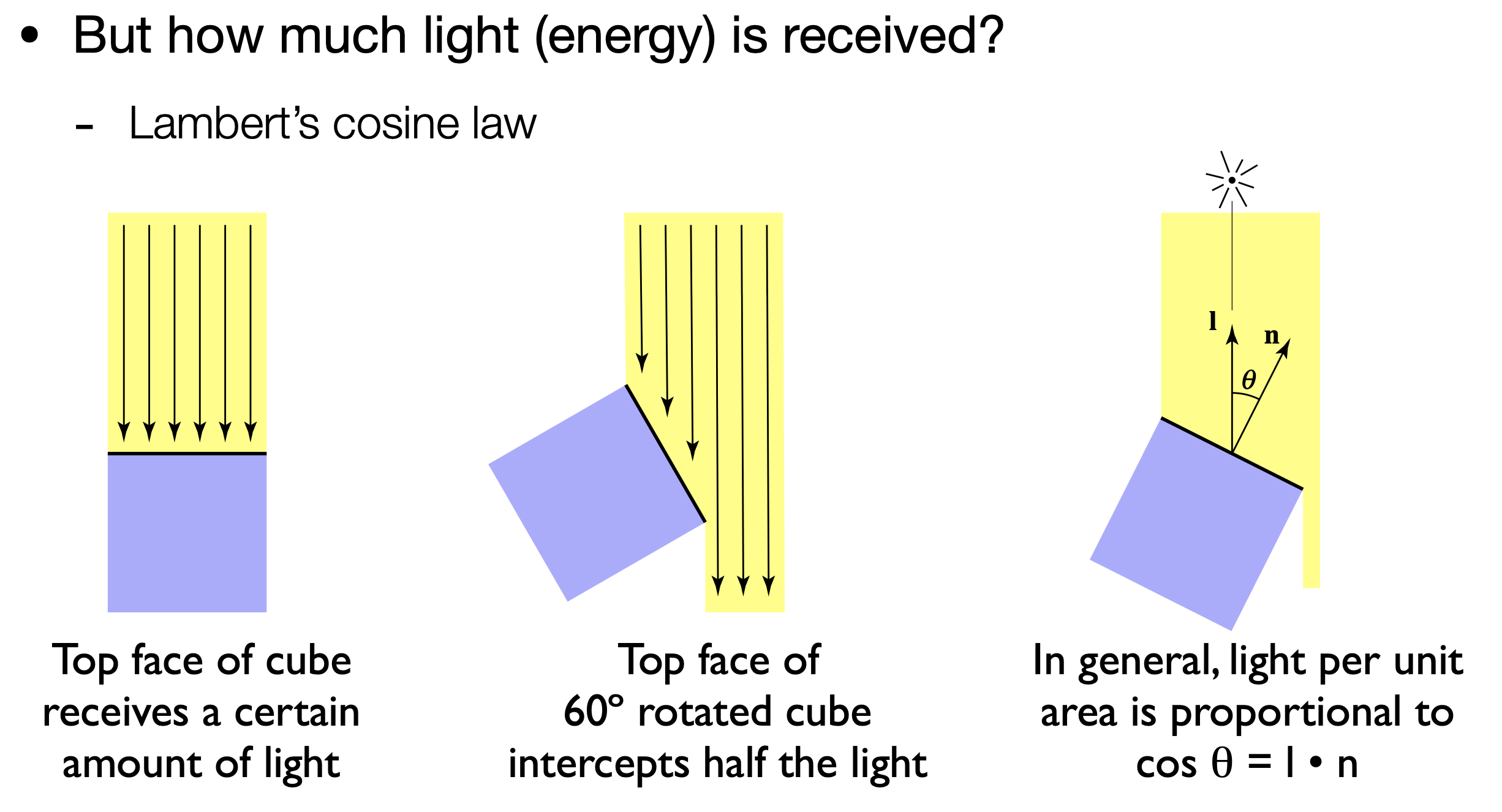
Light Falloff
- 能量守恒，远近球壳能量相等；平方反比
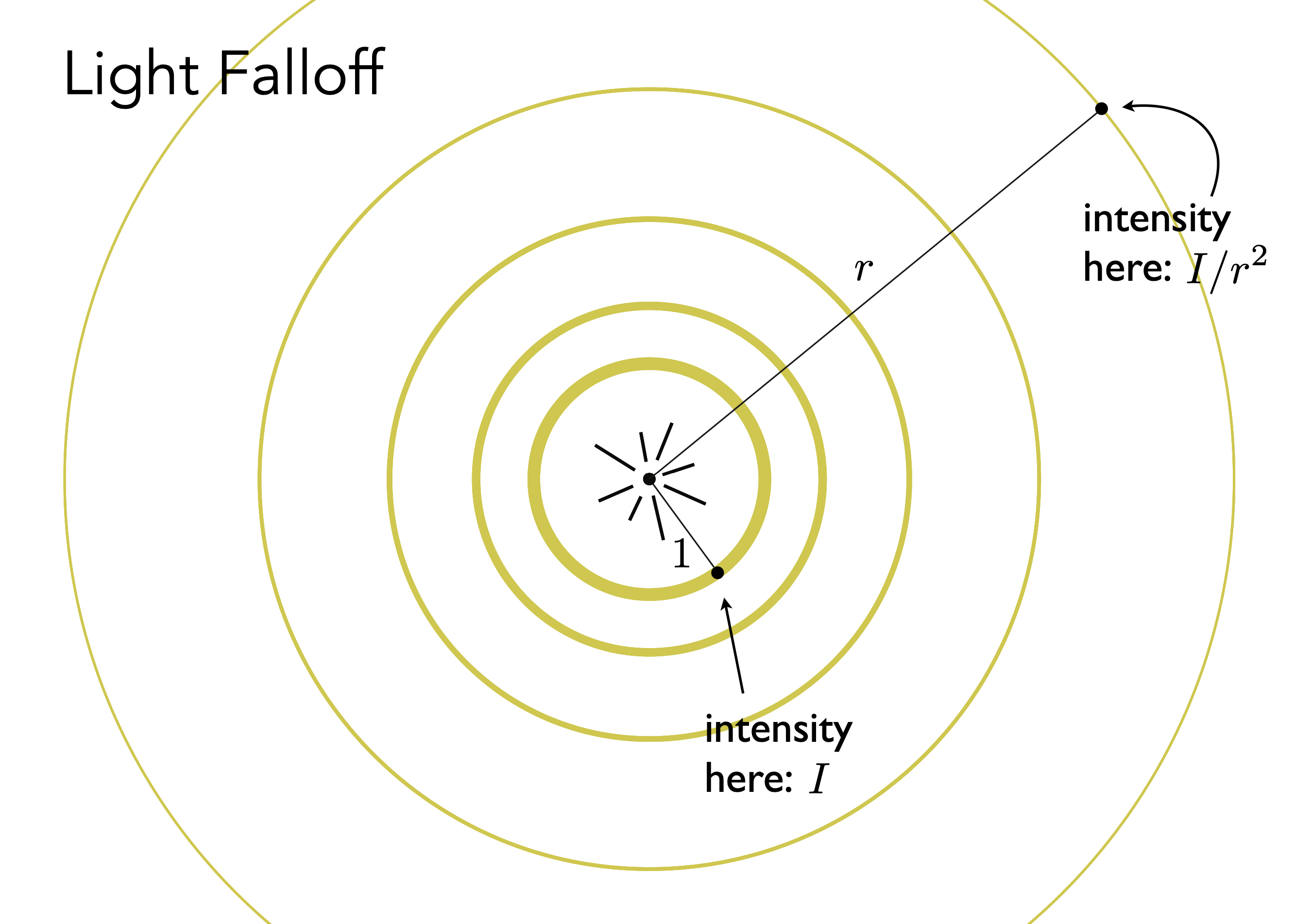
- - 推广：已知光源能量 & shading point与光源间距离，可知有多少光可传播到shading point；结合Lambert’s cosine law，可得出diffuse reflection的表示方法
Lambertian (Diffuse) Shading —— 漫反射最终着色
- 光源光强$I$，距离$r$，计算基于世界坐标
- $max(0, n \cdot l)$：避免$cos\theta<0$光照反向，无意义
- $k_d$漫反射系数，表示吸收和反射的能量，1白0黑，表示明暗；若$k_d$是vector3，则RGB三通道可表示颜色
漫反射理论上各个方向反射均匀，各个方向所观测到的着色应一致

P8 Shading (Pipeline and Texture Mapping)

Blinn - Phong Model

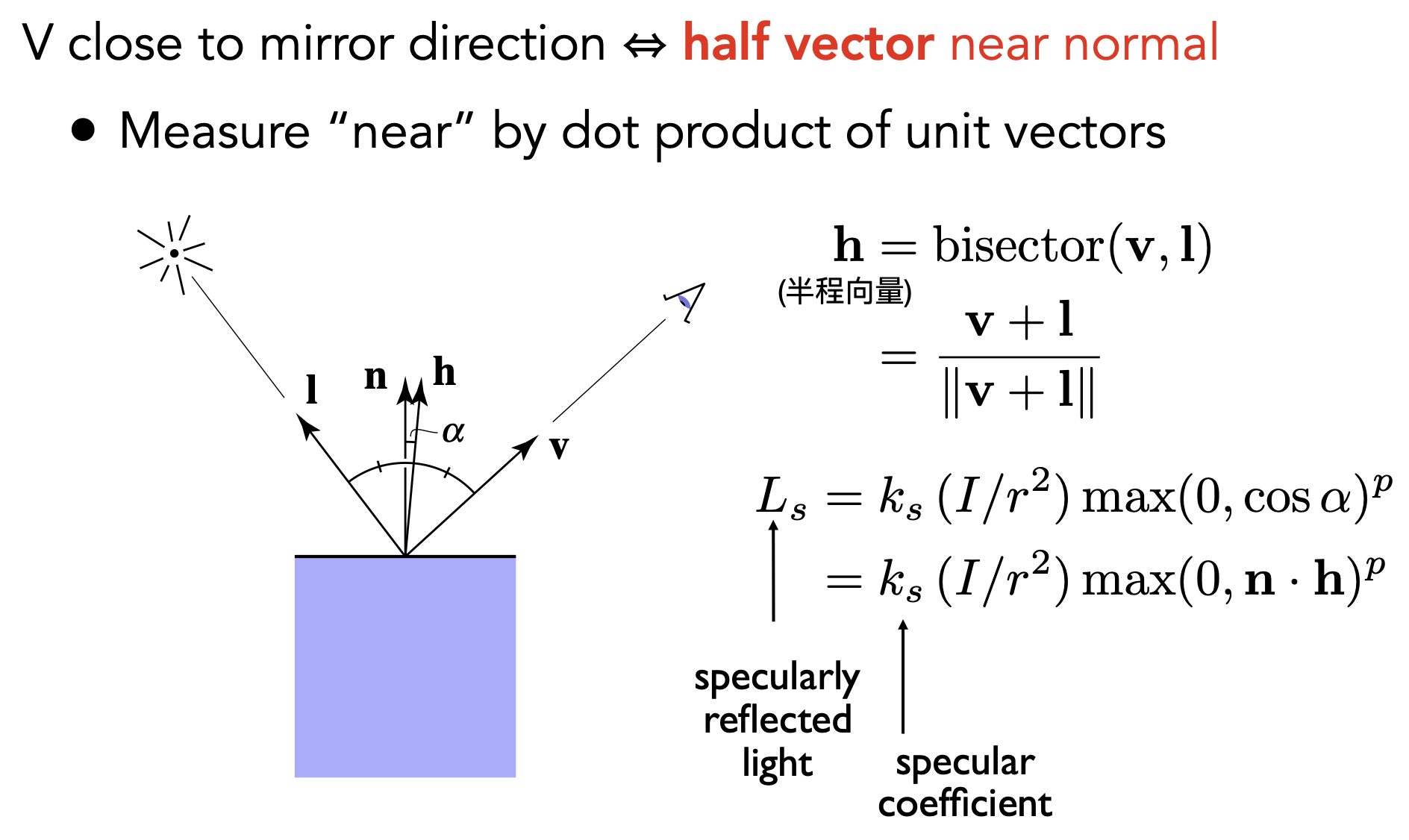
Specular Term 高光

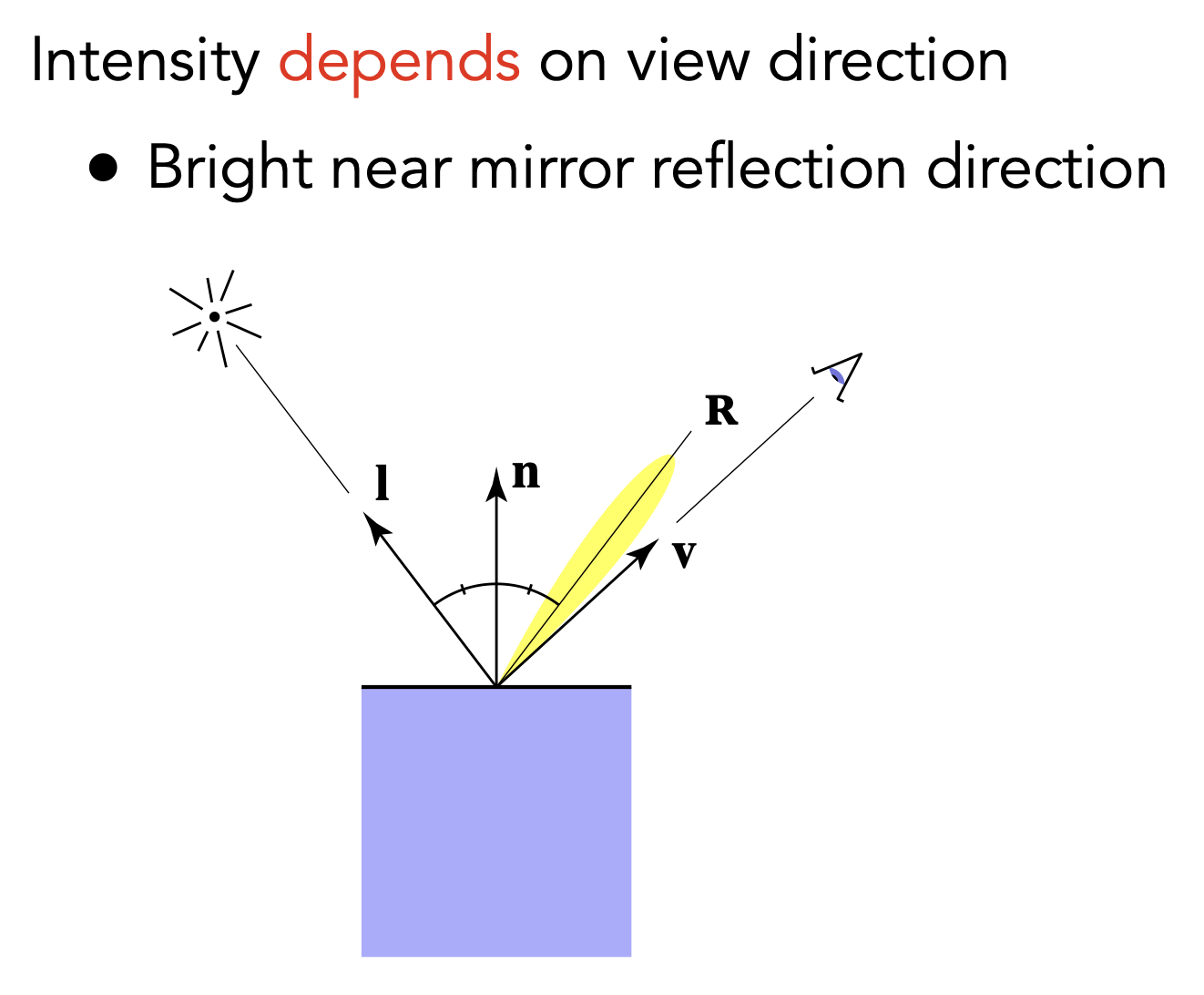
- $v$$和r$足够接近时，可得到高光项
Blinn - Phong 模型中的trick
- 备注：
  - $v$$和r$很接近$\iff$法线方向和半程向量($l$和$v$角平分线方向)很接近；$n\cdot h$越接近1，则观察到的镜面反射越强烈
  - 镜面反射系数$k_s$通常认为是白色的
  - 利用半程向量的Blinn - Phong模型是对计算反射方向$r$的简化计算。若直接$r\cdot v$，则是Phong模型。
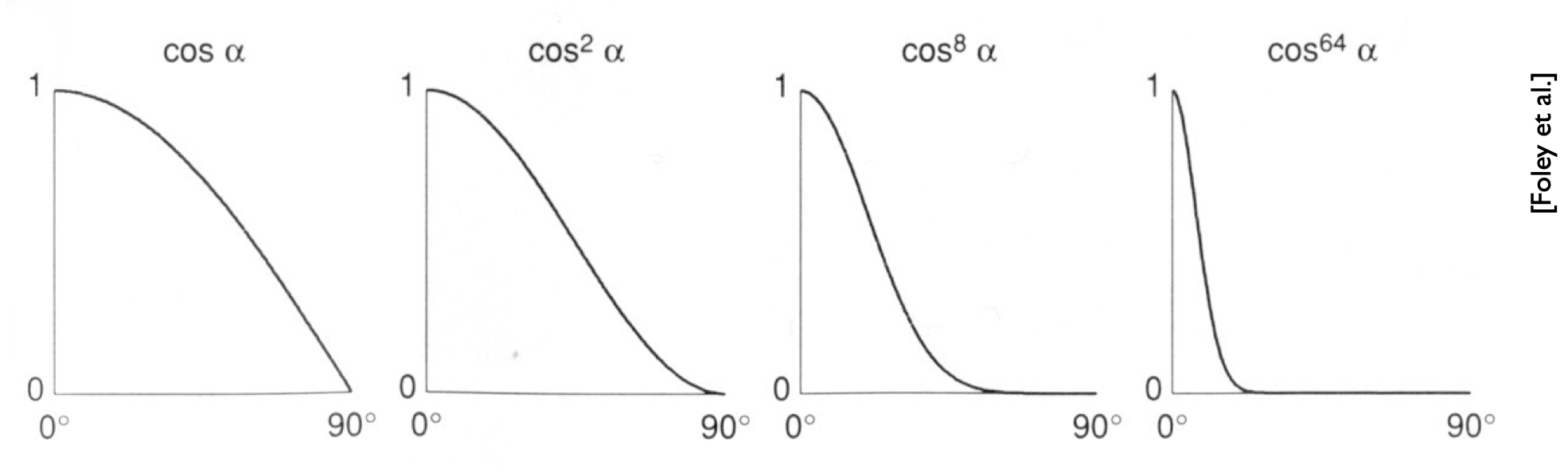
  - $max(0, n \cdot h)^p$指数$p$的作用：限制高光范围
    - 下图最左，不做指数运算，则会看到很大的高光；$p$通常为100~200
最终效果

Ambient Term 环境光

假设所有点接收到的环境光相同，强度$I_a$，来自四面八方；假设是错的！

最终效果

叠加所有光效

Shading Frequencies 着色频率

- 利用法线插值

Flat Shading: shade each triangle

- 每一个面都是平的，只有一个本身的法线
- 针对以一个三角面进行着色

Gouraud Shading: shade each vertex

- 求出顶点法线，针对每一个顶点进行着色
- 三个顶点所确定的三角形，根据三个顶点的颜色进行插值

Phong Shading: shade each pixel

- 得出三个顶点的法线后，插值三个顶点间每一个像素的法线方向，针对每个像素着色

对比

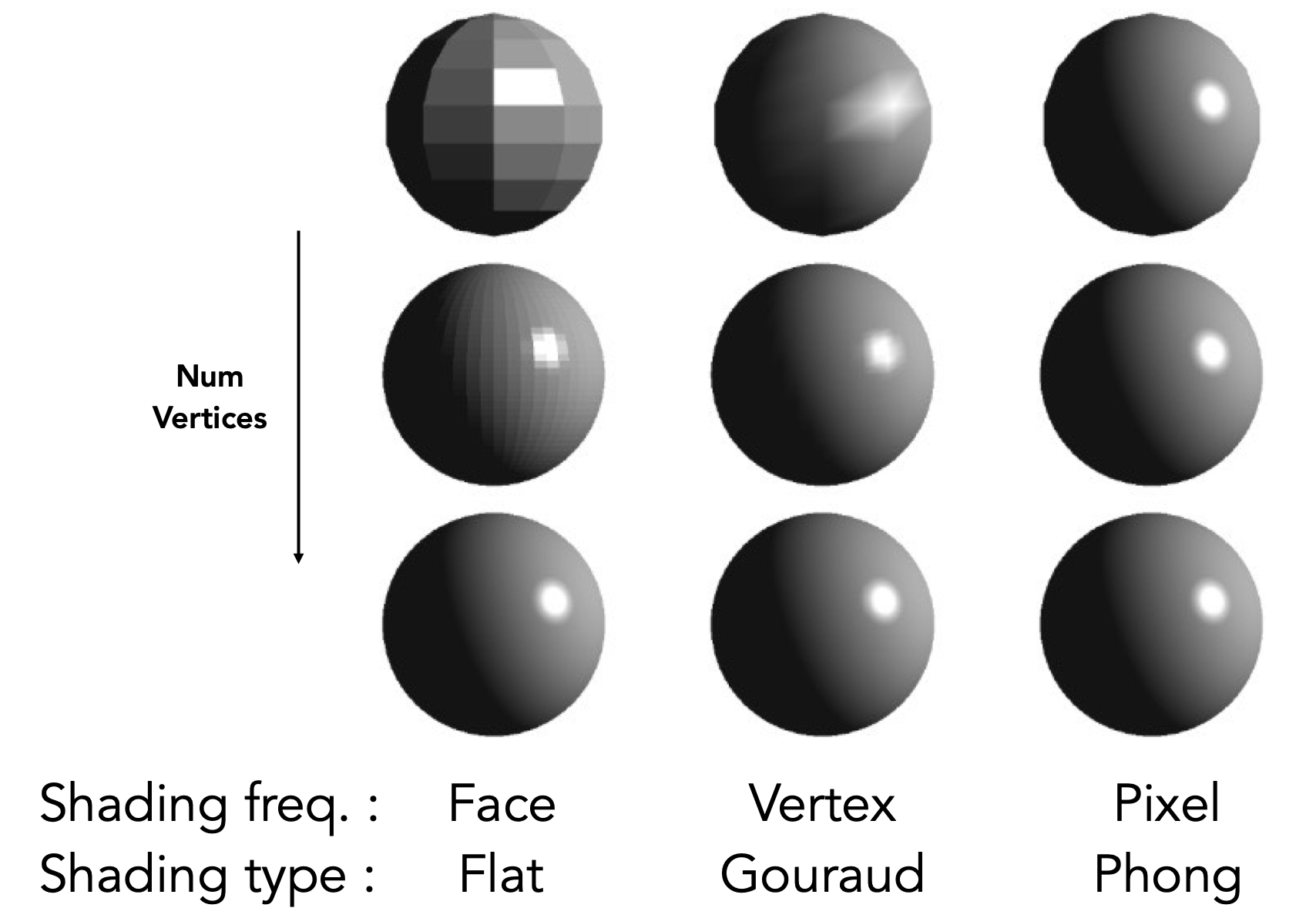
- 效果好坏是相对的
- 当面数极高，高于像素数，Flat shading消耗少于Phong shading，而效果差异不大

定义顶点法线方向

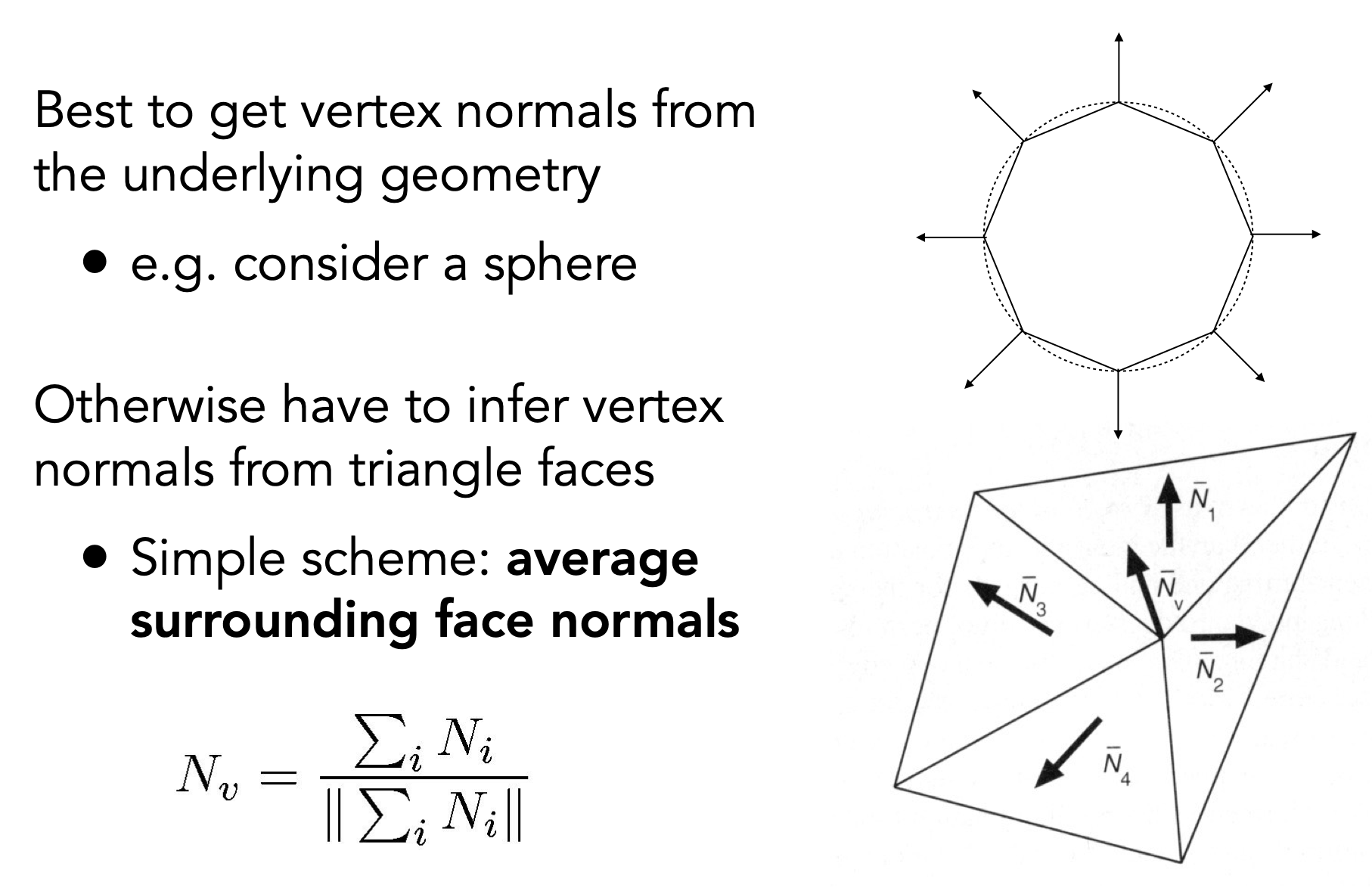
- 顶点法线：相邻面的法线方向加权平均(根据面积)，再归一化

定义像素法线方向

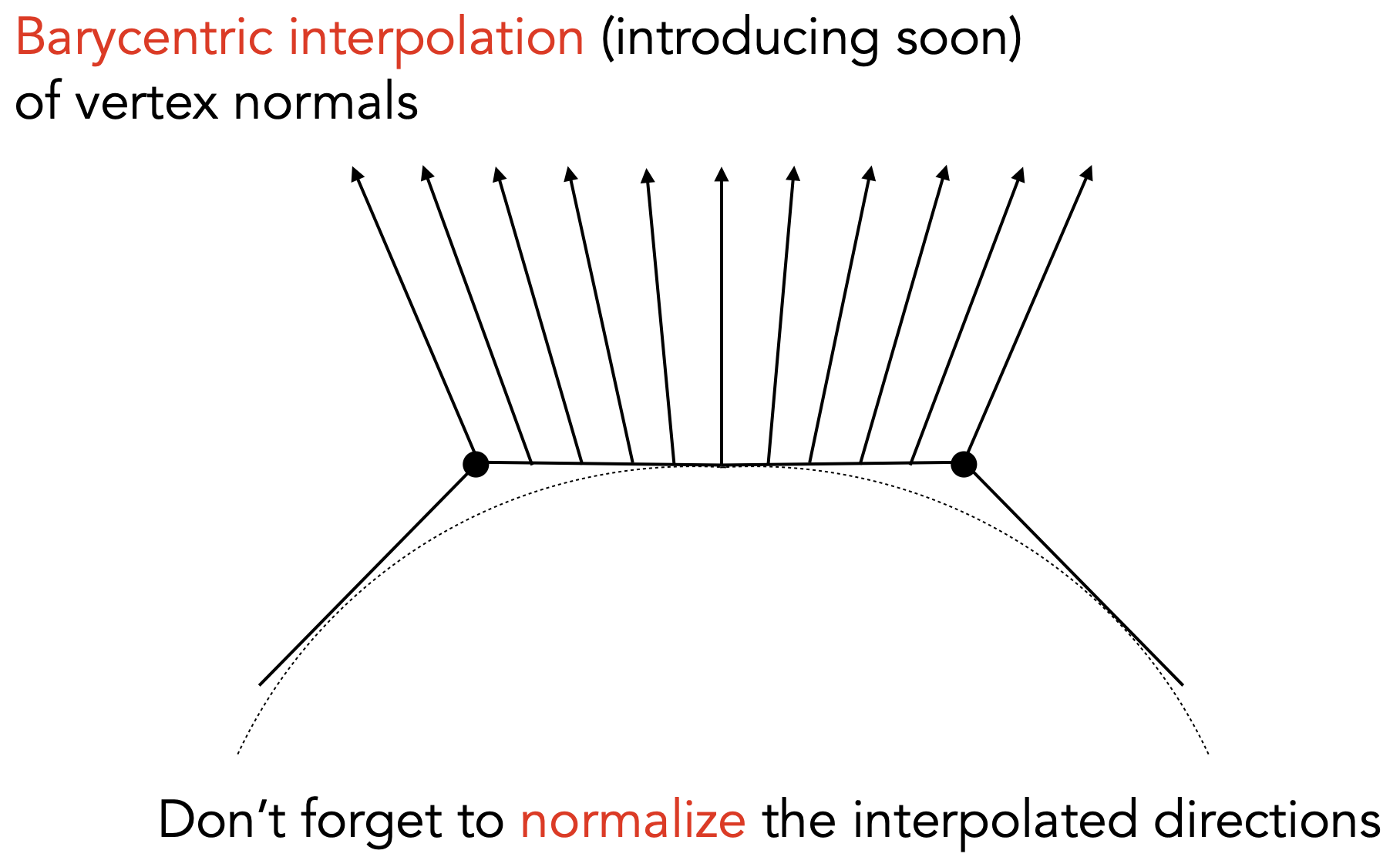
- 逐像素的法线：根据顶点法线，利用重心坐标(Barycentric interpolation)插值，而后归一化

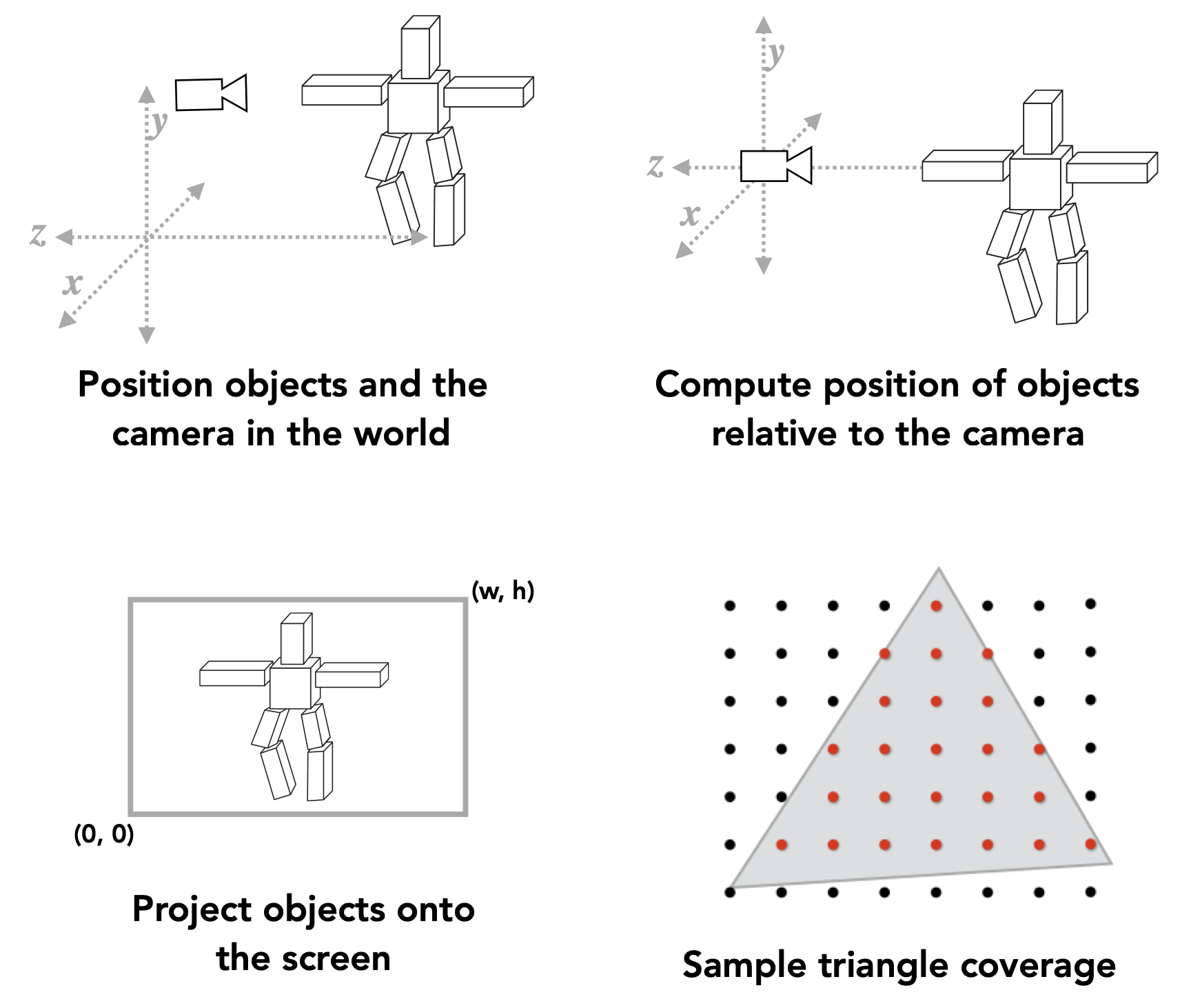
Graphics (Real-time Rendering) Pipeline 实时渲染渲染管线

渲染管线概述

概览
attention
- MVP变换发生在顶点阶段
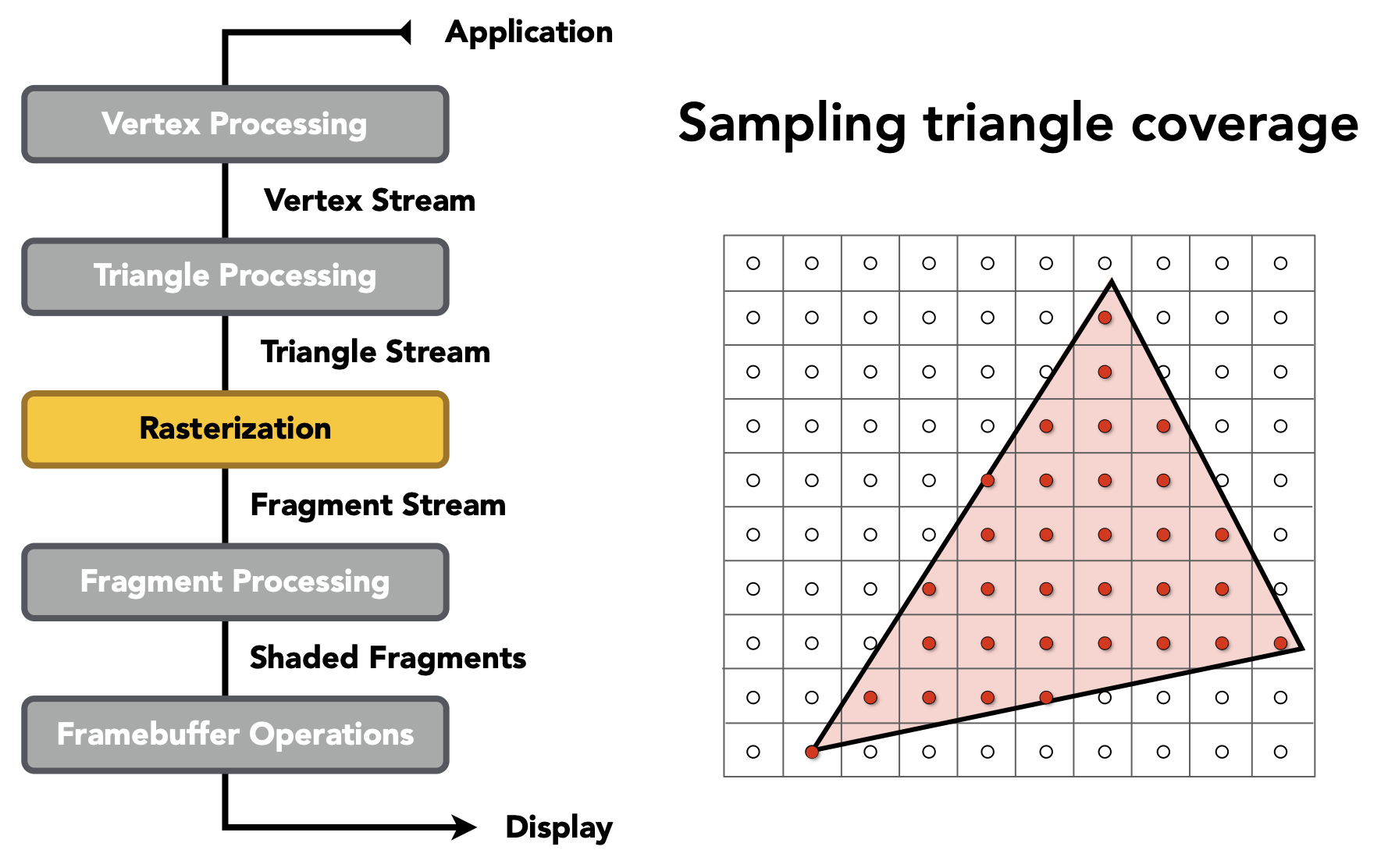
- 光栅化
- 深度缓存
- Shading可发生在不同阶段，顶点的着色发生在顶点阶段，像素着色发生在Fragment阶段
  - eg：Gouraud shading发生在顶点阶段；Phong shading发生在Fragment阶段（需像素产生后进行
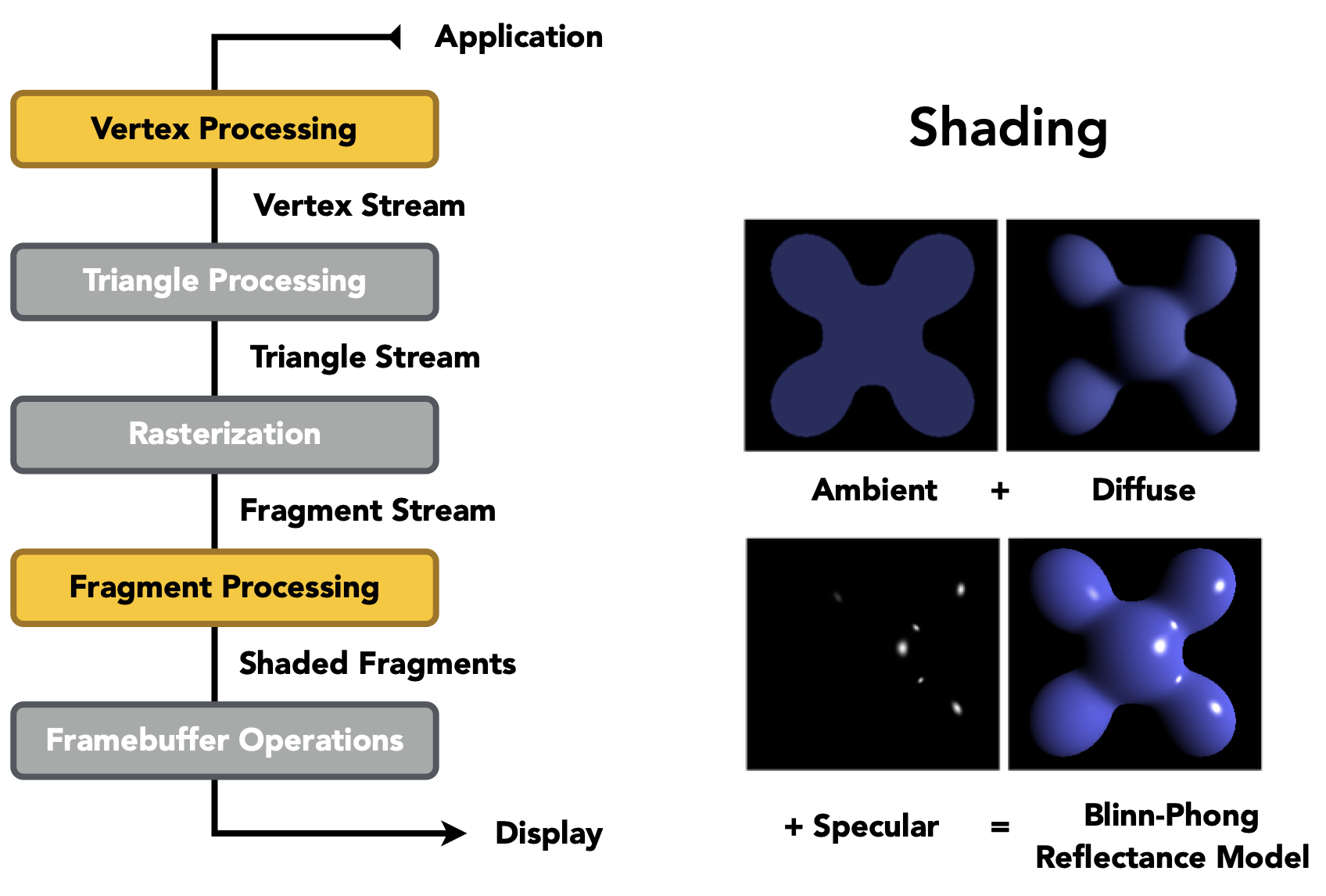
- Texture Mapping 纹理映射

Shader Programs

关于shader
- 本质是可以通过API在硬件上执行的语言
- 分顶点shader和fragment shader，每个顶点/fragment执行一次。shader程序对任何顶点/像素通用，不用for循环

一个像素着色器的例子

关于像素着色器：通过程序写出，如何计算出像素最终的颜色，并输出

uniform sampler2D myTexture;    // program parameter；纹理全局变量
uniform vec3 lightDir;    // program parameter；光照方向全局变量
varying vec2 uv;    // per fragment value (interp. by rasterizer)；插值
varying vec3 norm;    // per fragment value (interp. by rasterizer)；插值
void diffuseShader()
{
    vec3 kd;    // 漫反射系数
    kd = texture2d(myTexture, uv);    // material color from texture 

    // Phong模型漫反射计算
    kd *= clamp(dot(–lightDir, norm), 0.0, 1.0);    // Lambertian shading model；认为入射方向向内，因而lightDir为负

    gl_FragColor = vec4(kd, 1.0);    // output fragment color
}

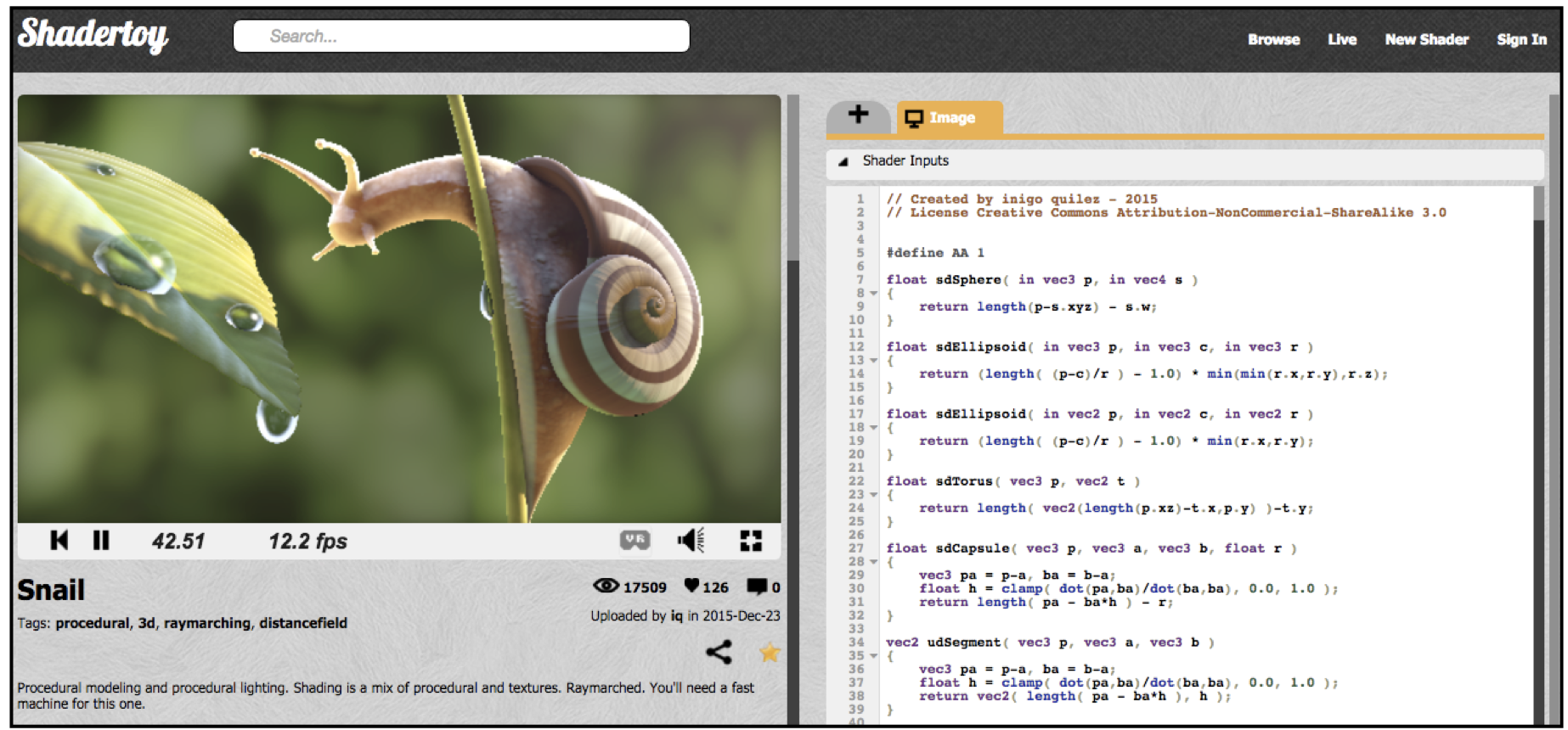
IQ大神的shader：Inigo Quilez, http://shadertoy.com/view/ld3Gz2
- 大神博客：https://iquilezles.org/
- 大神油管：https://www.youtube.com/@InigoQuilez

Texture Mapping 纹理映射

注意⚠️：接下来的配图有点儿掉san🥵
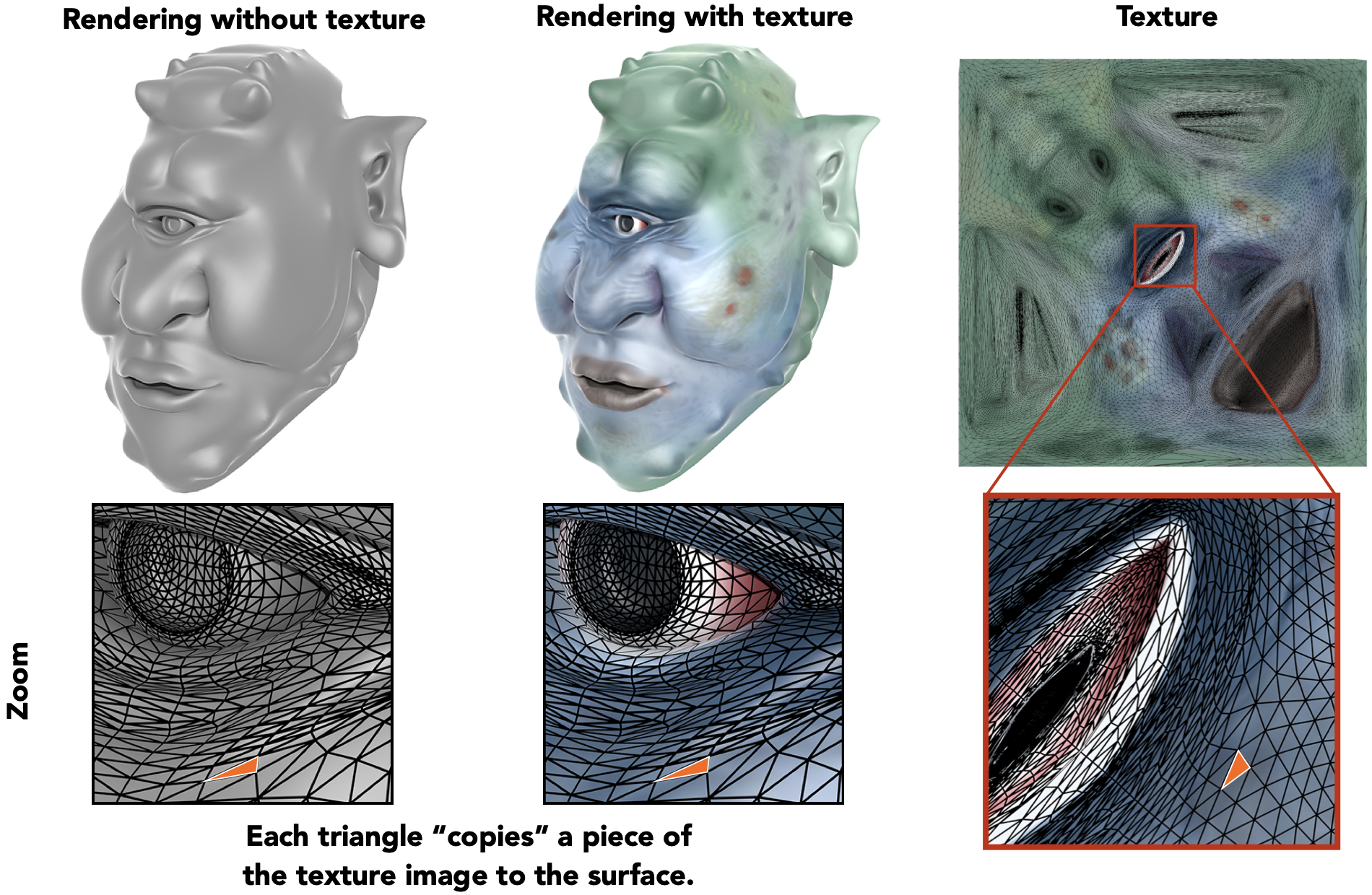
思路：共用同一个模型，但漫反射系数发生了改变；需寻找一种方法，定义一个物体上任意一点的属性
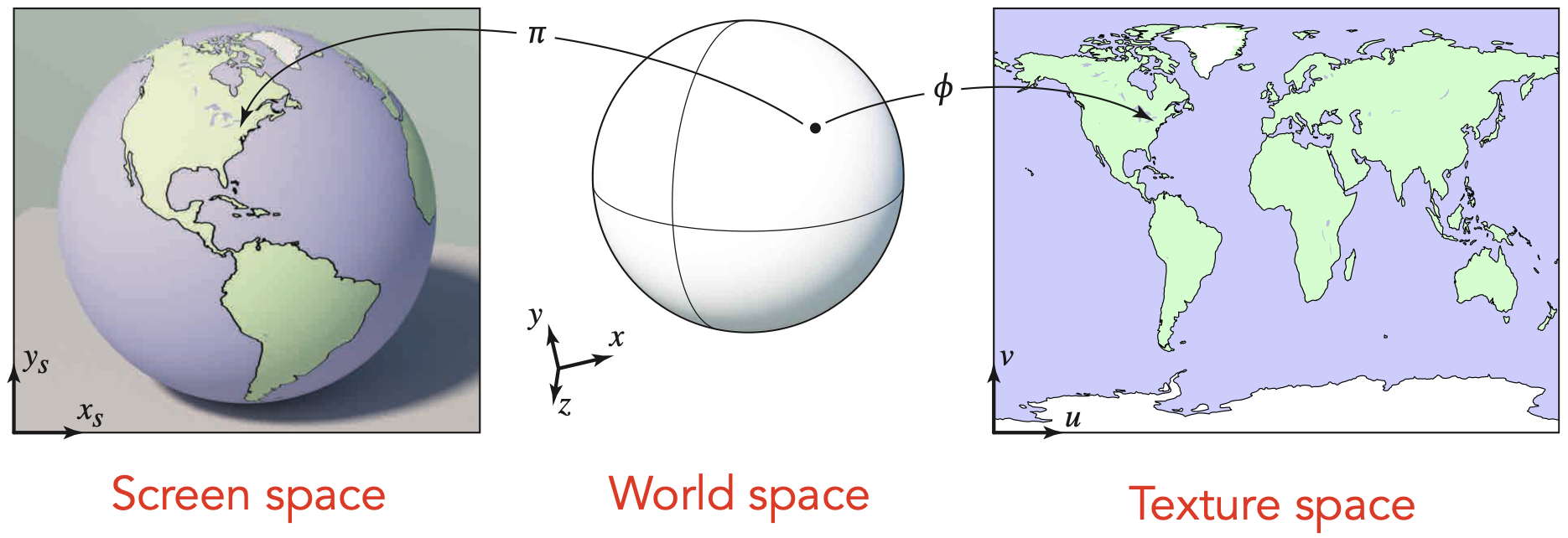
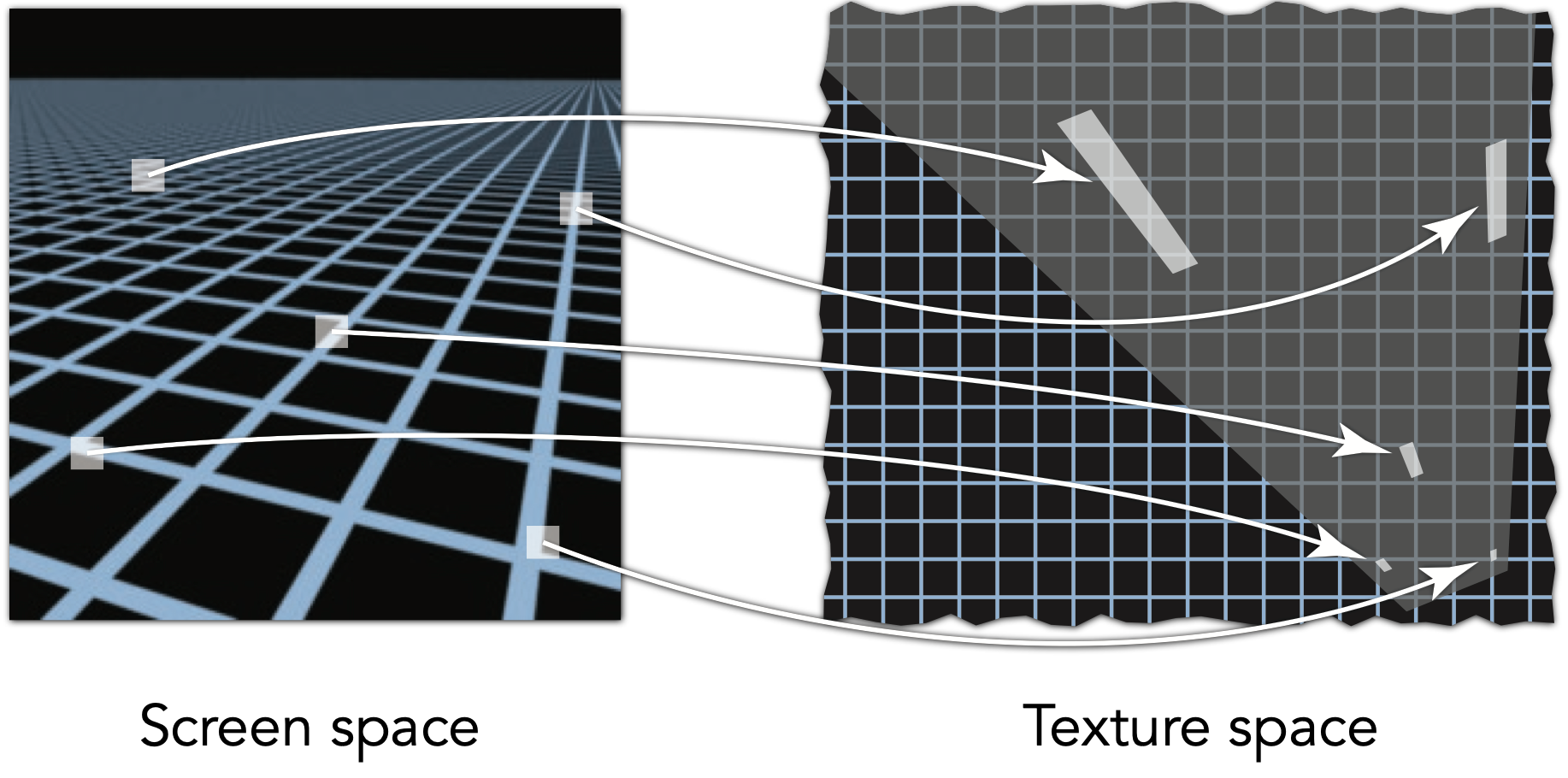
Surfaces are 2D: Every 3D surface point also has a place where it goes in the 2D image (texture).
Texture Applied to Surface
Visualization of Texture Coordinates
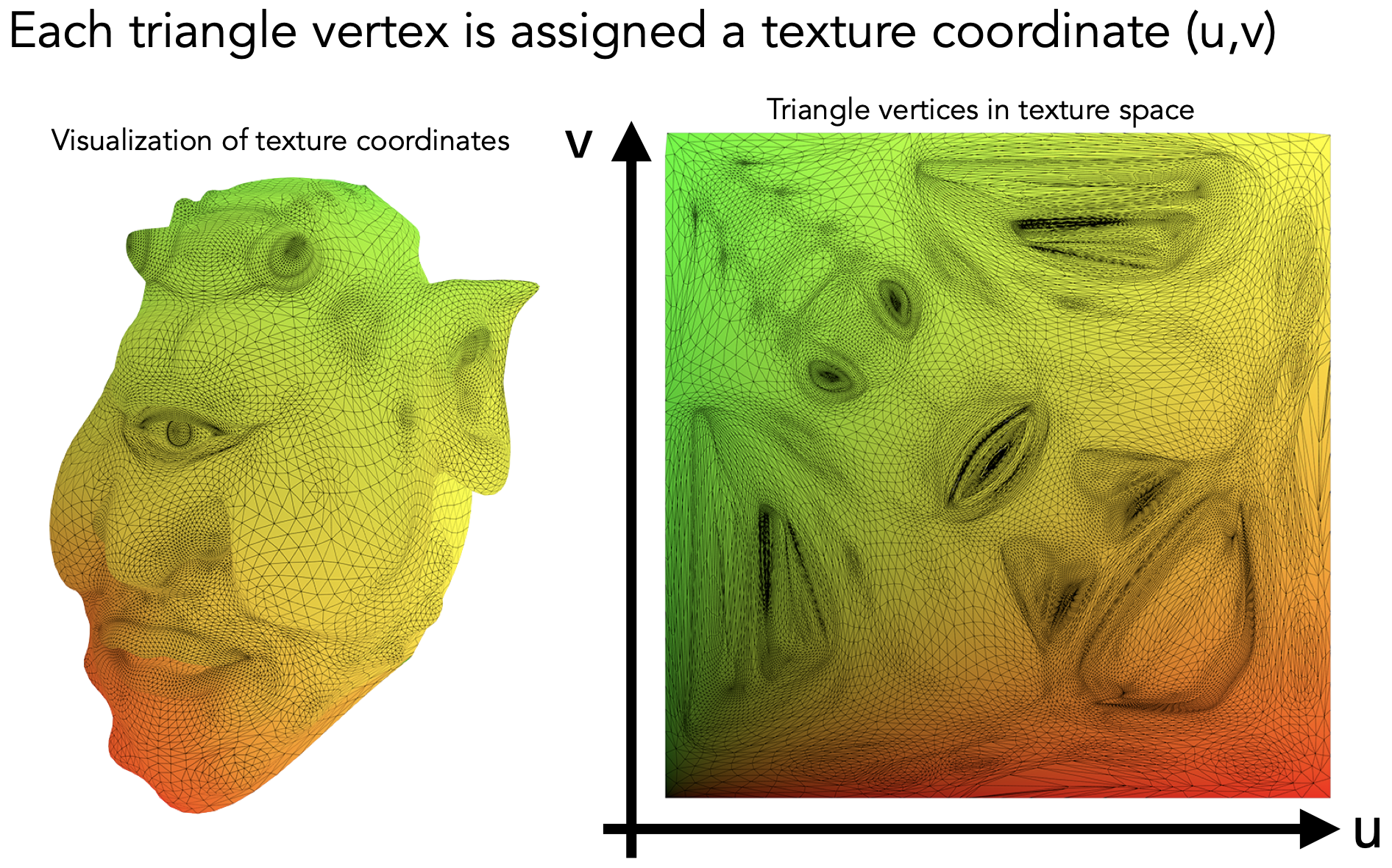
- uv纹理范围在$(0,1)$
Texture Applied to Surface
纹理被重复利用
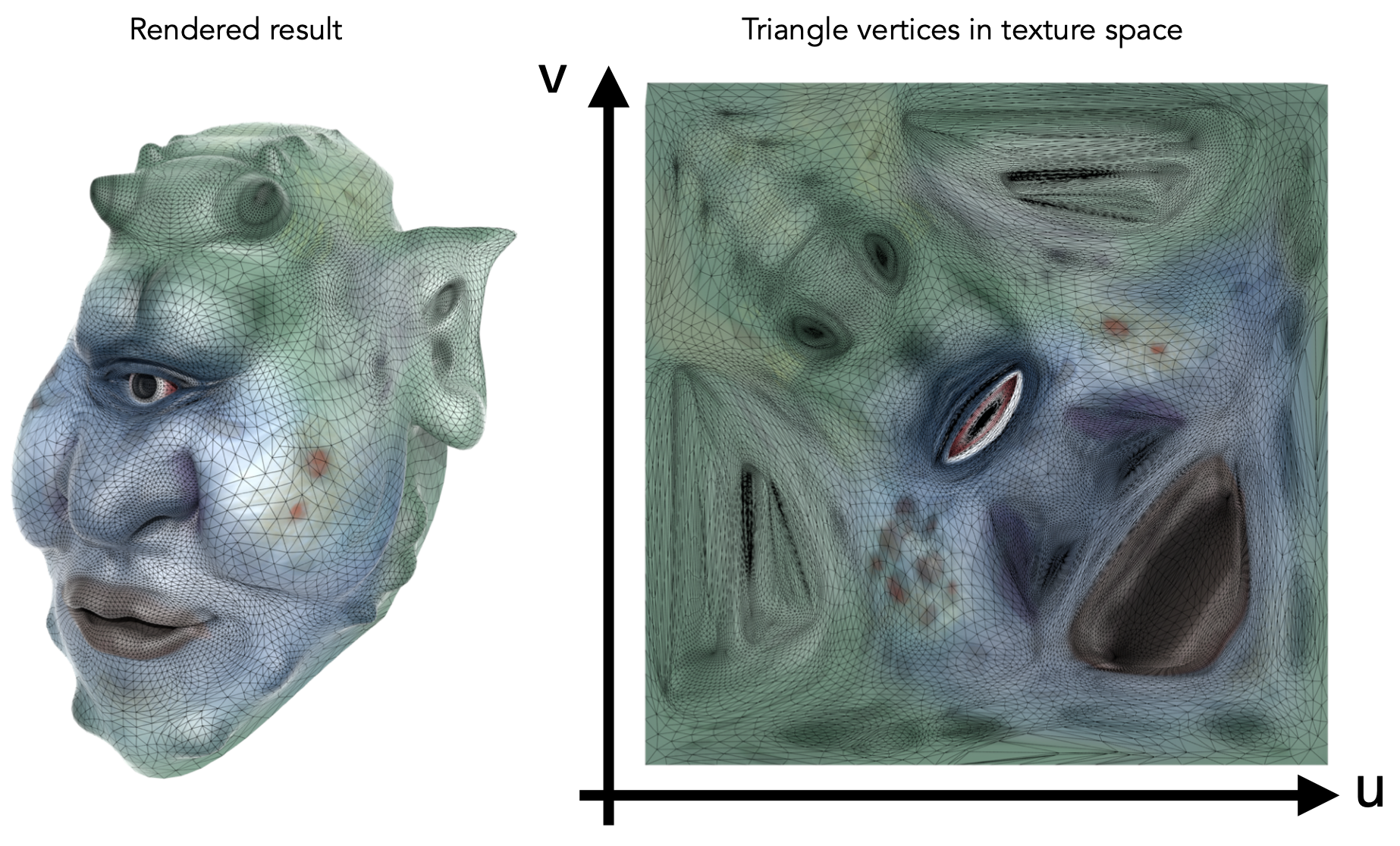
关于三角形内部点的uv值：通过顶点uv和重心坐标插值得出

P9 Shading (Texture Mapping cont.)

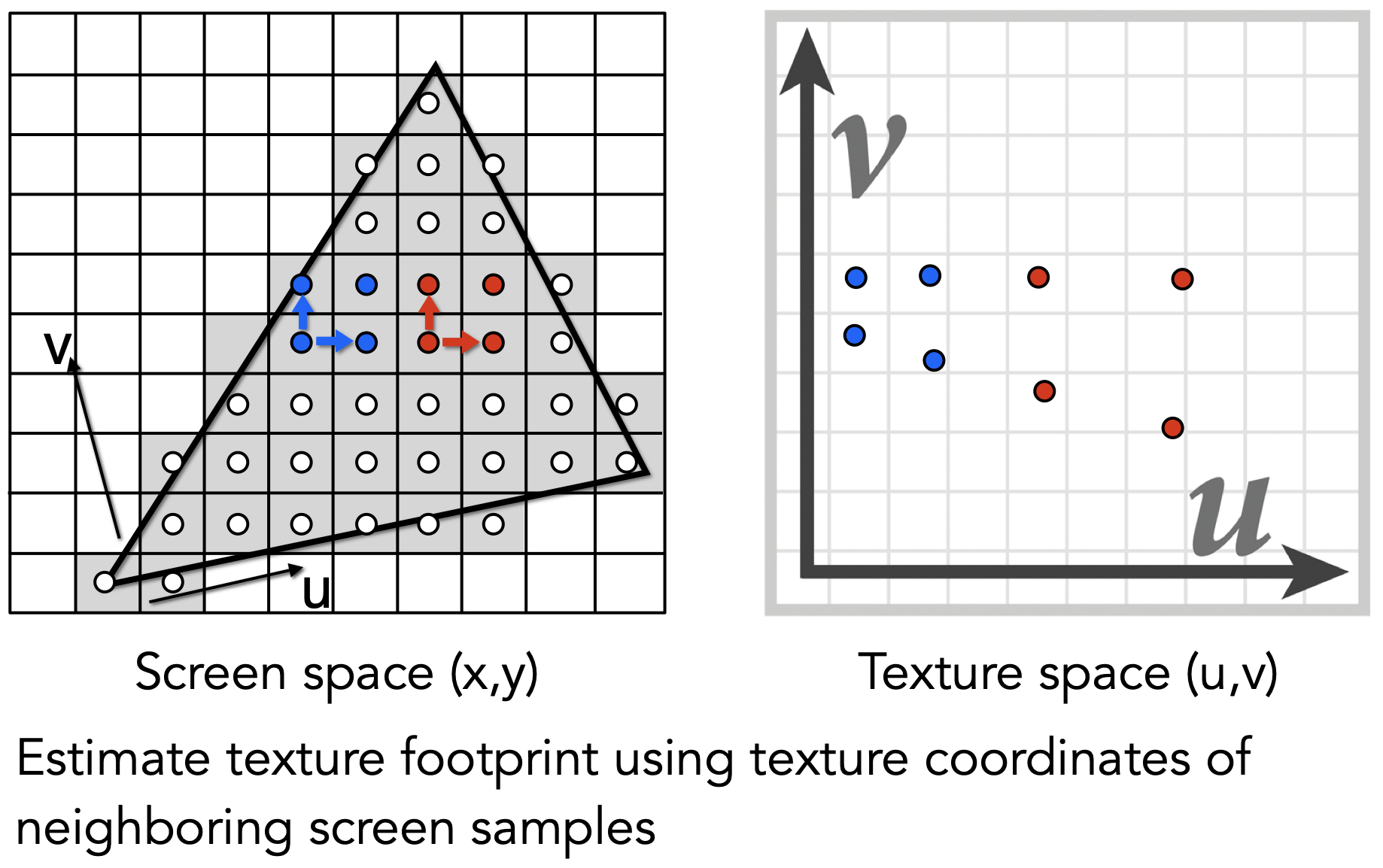
Interpolation Across Triangles: Barycentric Coordinates 重心坐标

三角形内部插值的作用：通过顶点的值，完成顶点间片元（像素）的平滑过度
插值的内容：texture coordinates, color, normal vectors…
重心插值数学基础
- 重心坐标概念基础
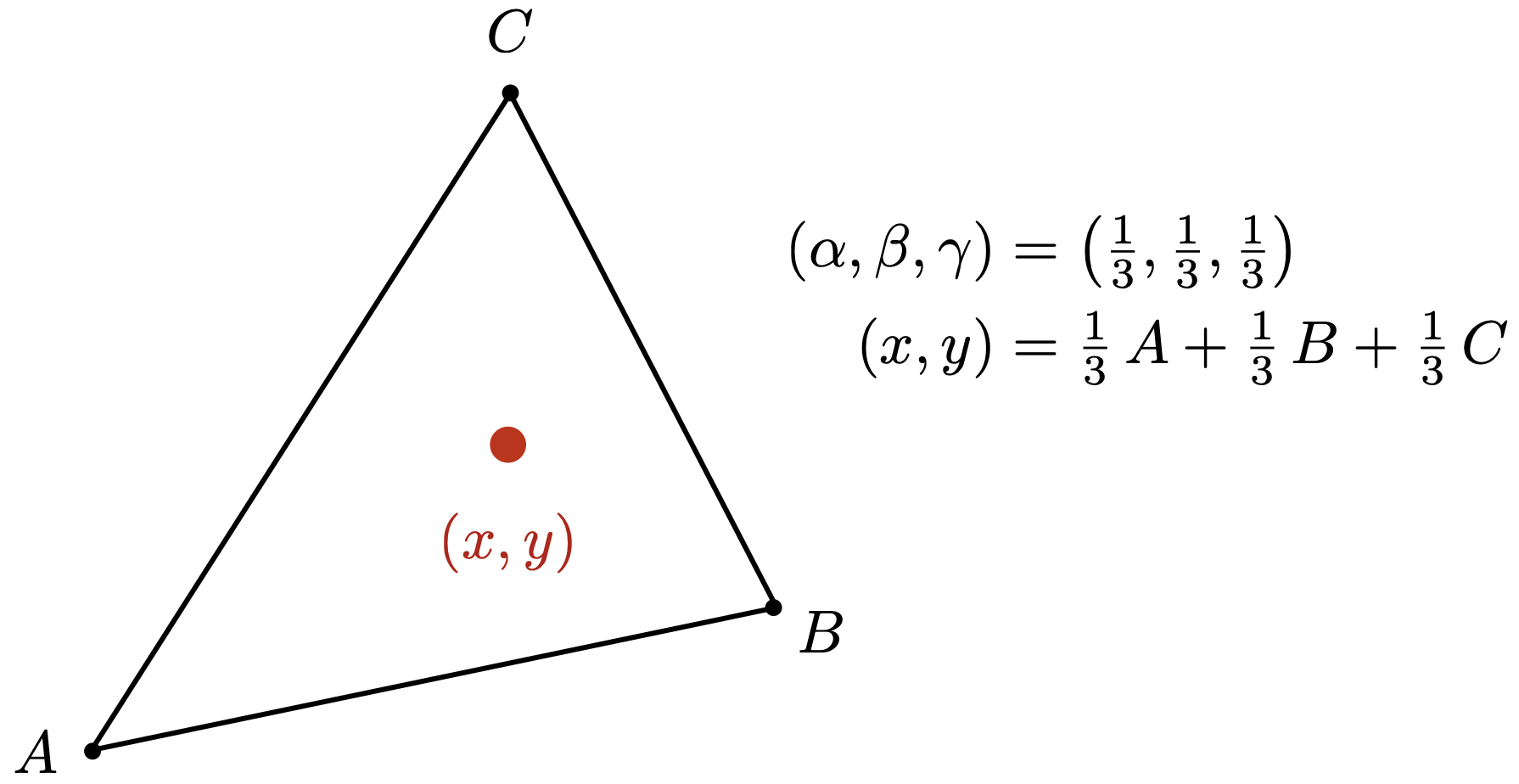
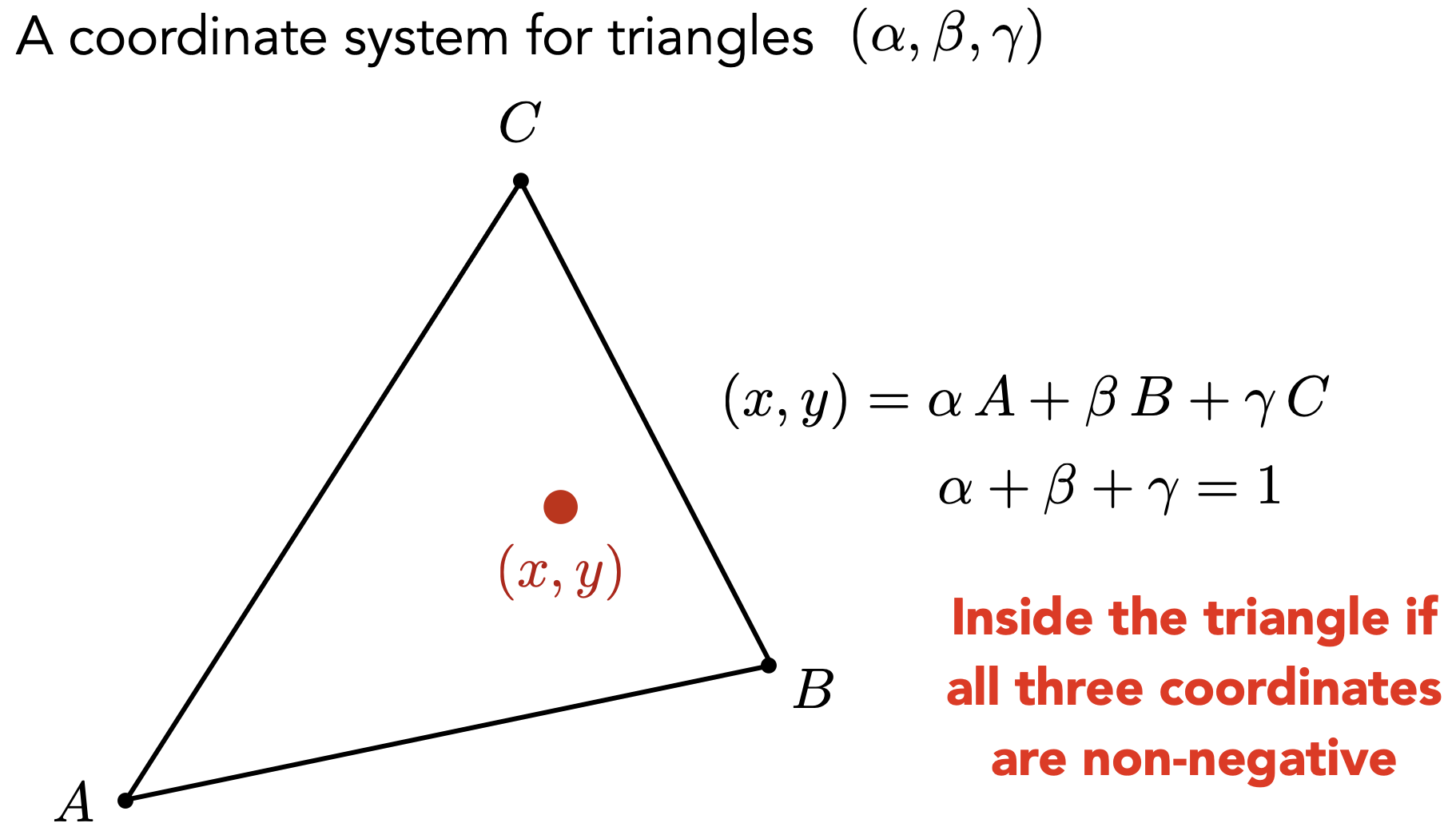
  - 三角形内任意一点$(x,y)$都可以写成三个顶点的线性组合：$(x,y) = \alpha A+\beta B + \gamma C$；其中，$\alpha + \beta + \gamma = 1$，且$\alpha,\beta,\gamma > 0$。重心坐标即为$(\alpha,\beta,\gamma)$
  - $\alpha + \beta + \gamma = 1$表明点在三角形所在平面内，$\alpha,\beta,\gamma > 0$表明点在三角形内部
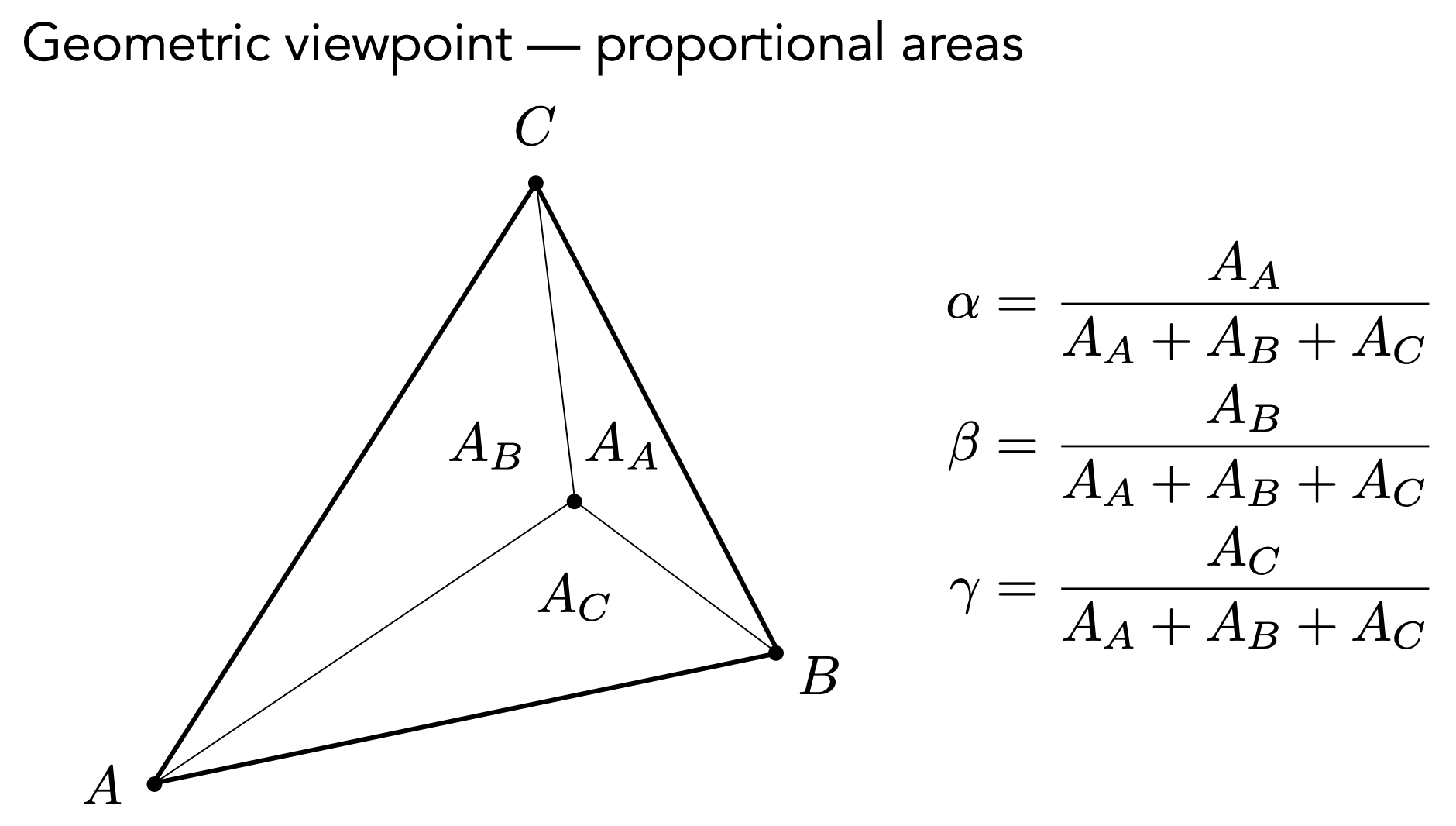
- 重心坐标求法：利用面积
- 三角形自身重心的性质：重心与三角形顶点连线所得的三角形面积相等。可得：
- 导出公式
三角形内重心坐标的应用
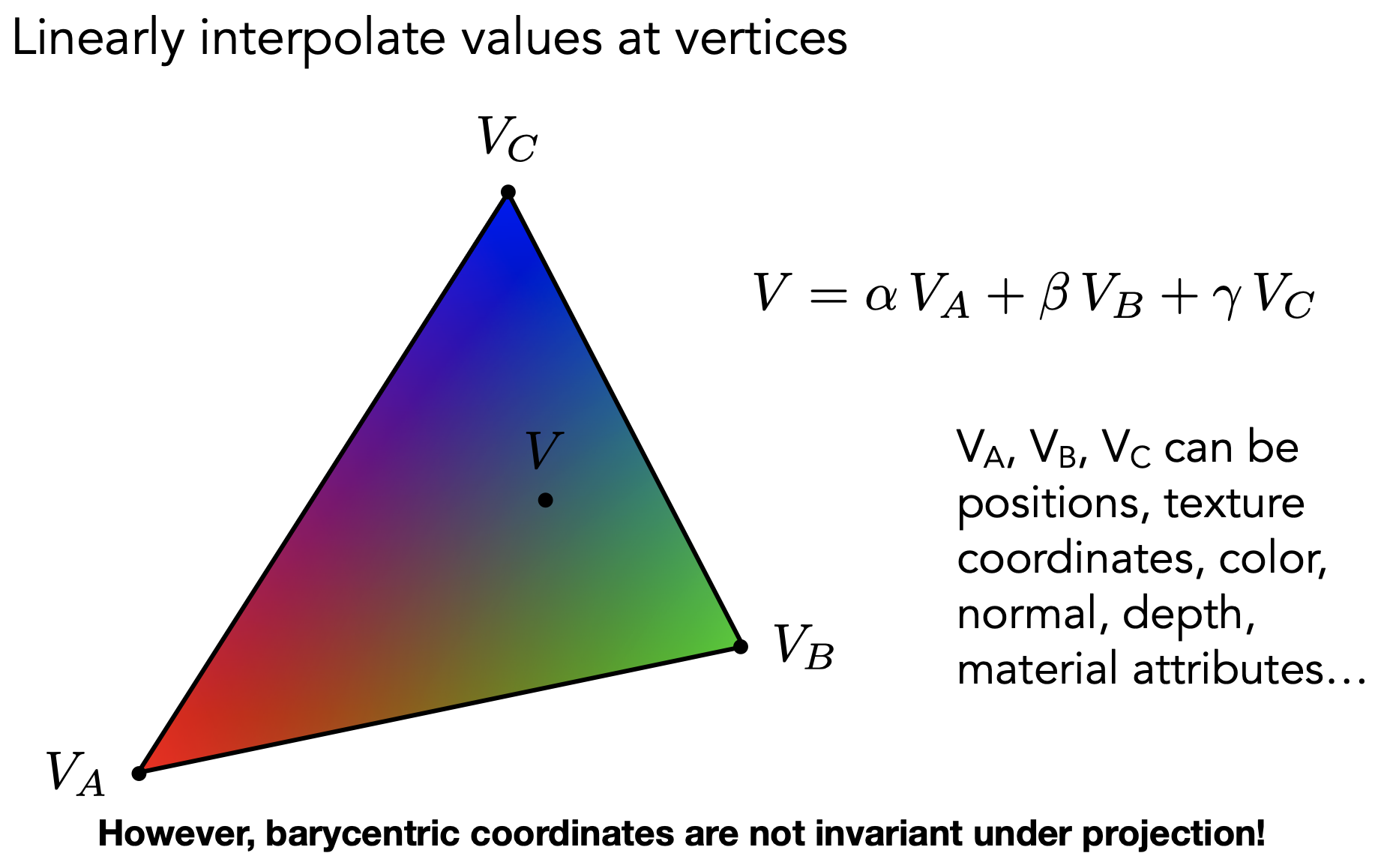
- - 注意⚠️：三角形投影后形状发生拉伸，重心坐标会改变。三维空间中三角形应在三维空间中插值，不能在二维投影屏面插值。

Applying Textures 纹理应用

纹理映射举例——Diffuse Color
- 通过对顶点插值，得出每一个片元(x, y)的uv坐标；
- 随后在纹理上查询该片元uv值，得出该片元的颜色texcolor；
- 将漫反射系数$k_d$设置为texcolor。

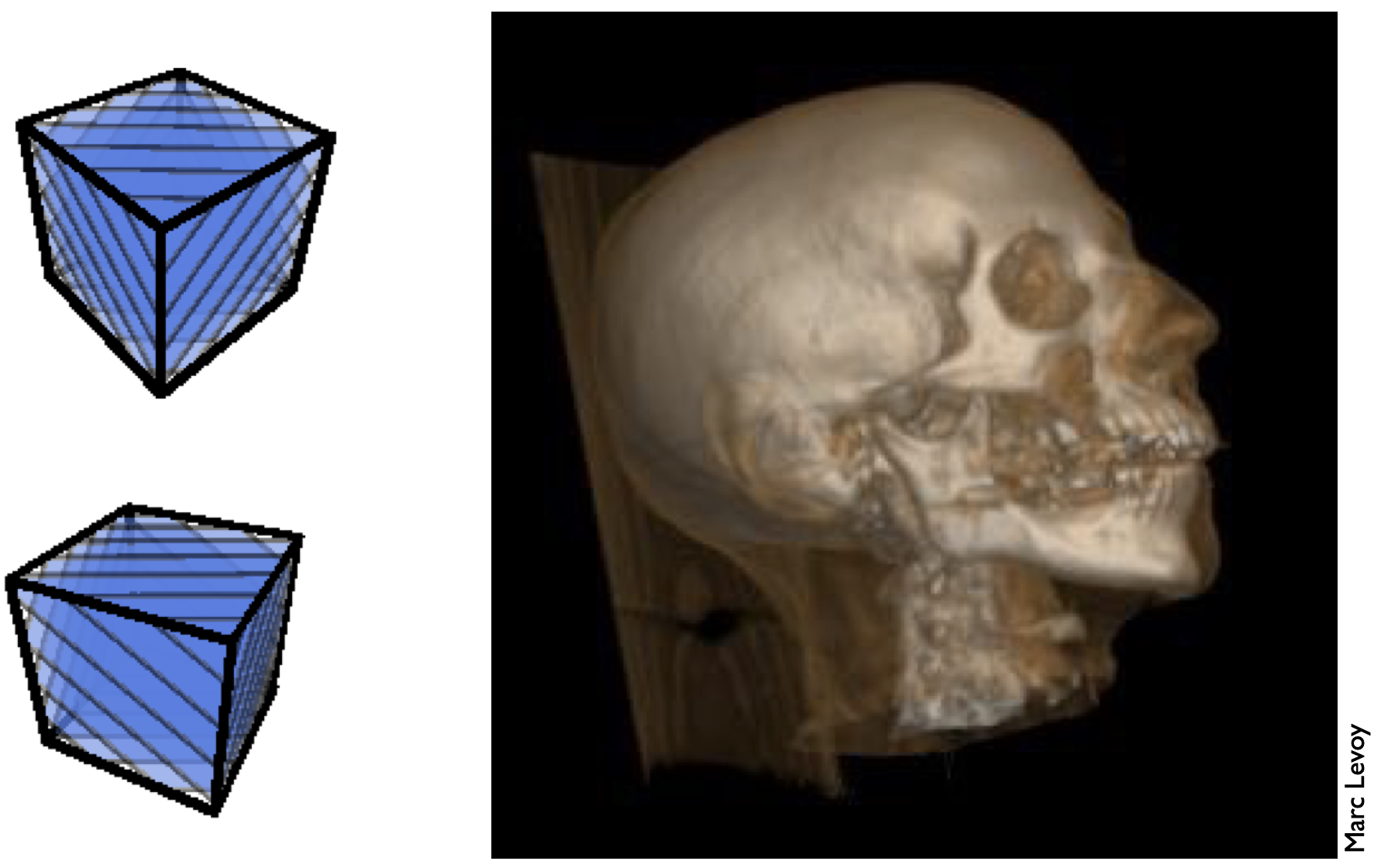
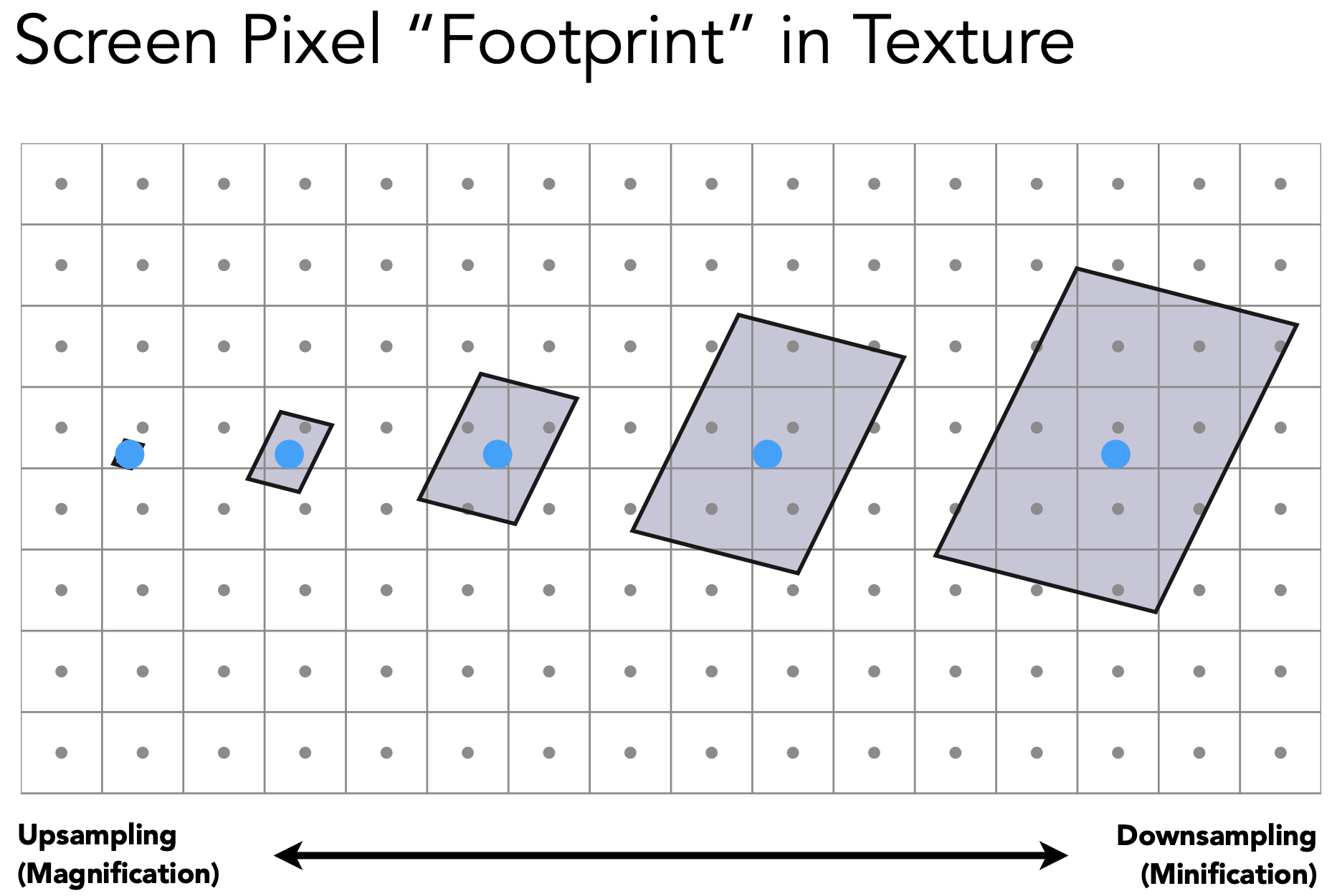
Texture Magnification(纹理分辨率小，需放大)

插值方法：Nearest, Bilinear, Bicubic

Nearest

屏幕pixel颜色应用最近的纹理texel的颜色，导致多个相邻pixel被映射成一个texel

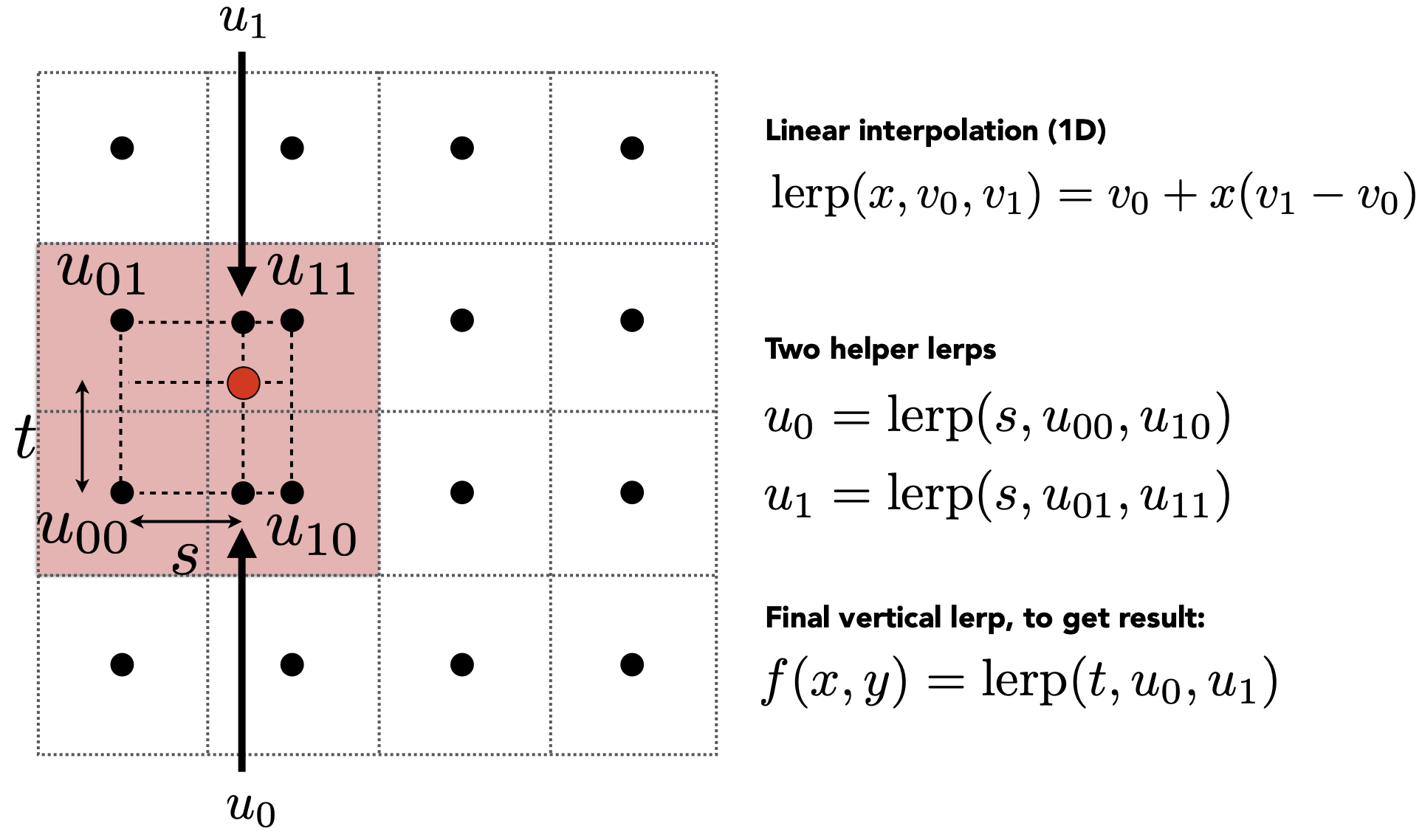
Bilinear Interpolation 双线性插值

寻找一个pixel(红色)附近的四个texel(黑色)，定义$t$和$s$范围都为$(0,1)$
由此插值后，$u_{00},u_{01},u_{10},u_{11}$四个texel所围成的区域内，pixel可实现平滑过度

Bicubic Interpolation

利用pixel附近的十六个texel，进行三次的插值

Texture Magnification(纹理分辨率大，需缩小)

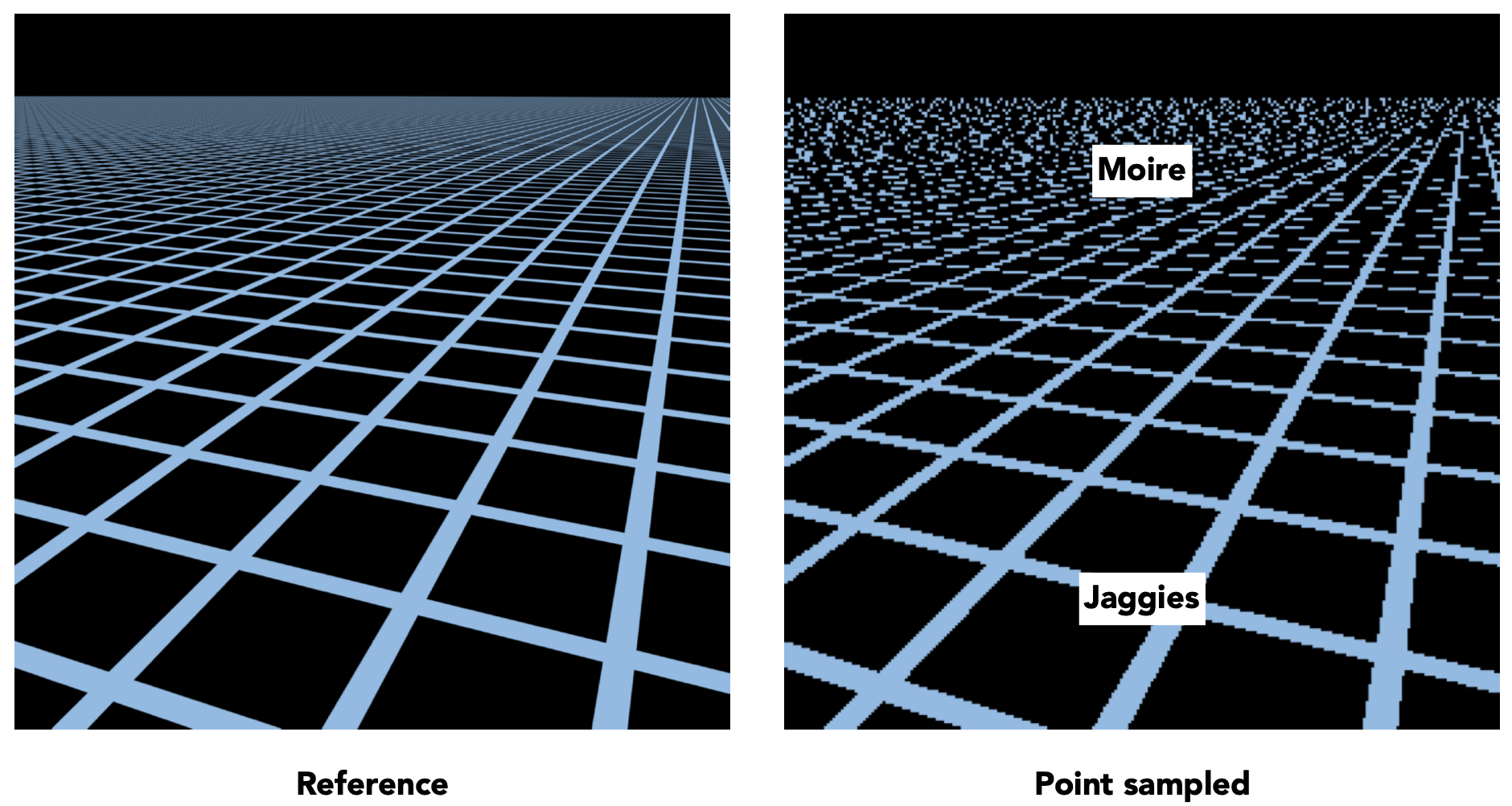
问题：产生摩尔纹和锯齿
Antialiasing — Supersampling 超采样？
- 可以，但消耗太大
- 当纹理严重缩小时，多个texel会集中在一个pixel中。一个pixel中，信号频率太快，而采样频率跟不上
采样会引起走样，因此引入不采样的思路。
- 理想：可直接得知像素覆盖的texel的平均值$\Rightarrow$给定任何一个texel区域即可得知平均值
- 引入Range Query范围查询

Mipmap: Allowing (fast, approx., square) range queries

Intro

mipmap做近似的、正方形的查询
如下图，Level提升以及，分辨率减半

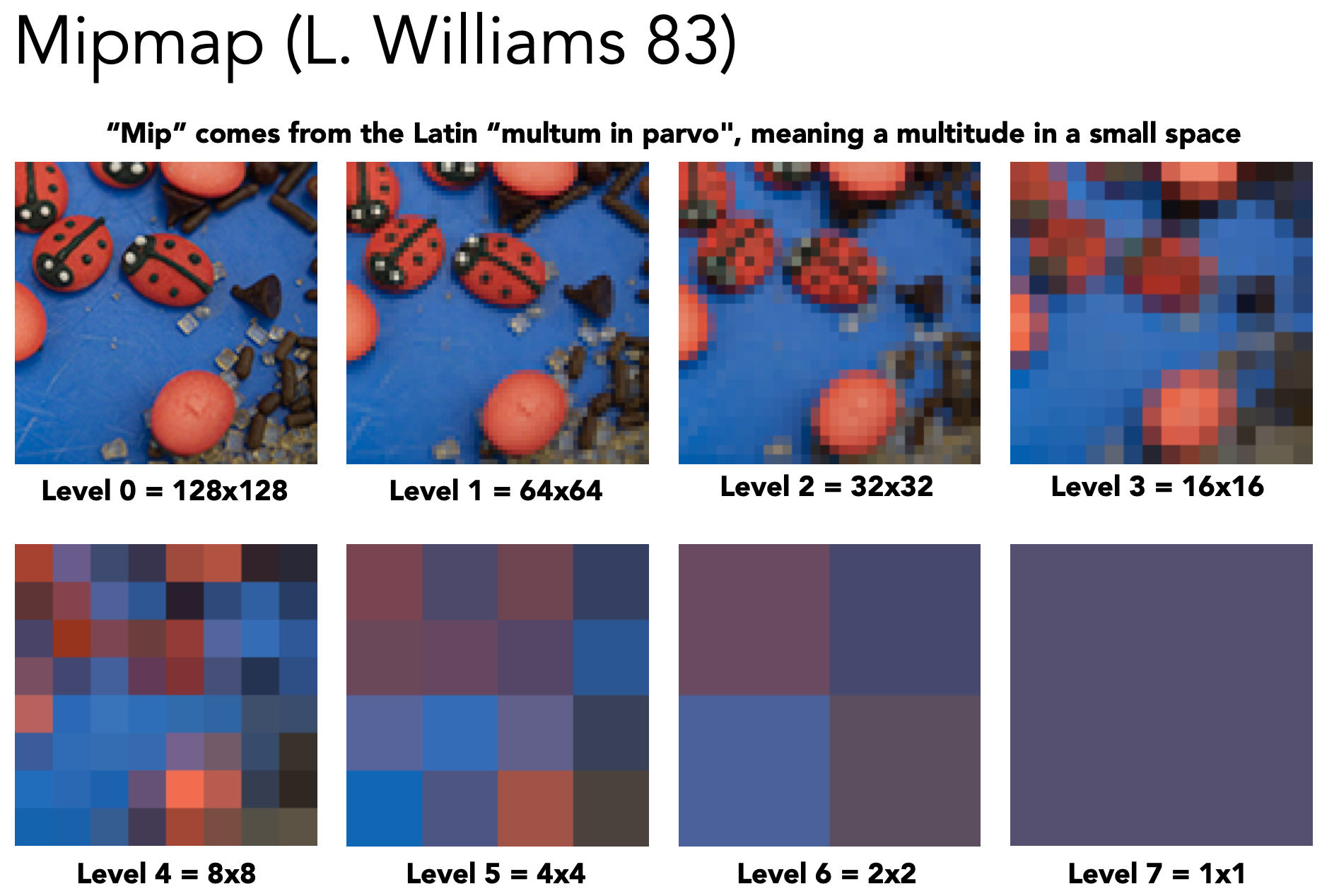
截屏2023-04-13 20.07.23

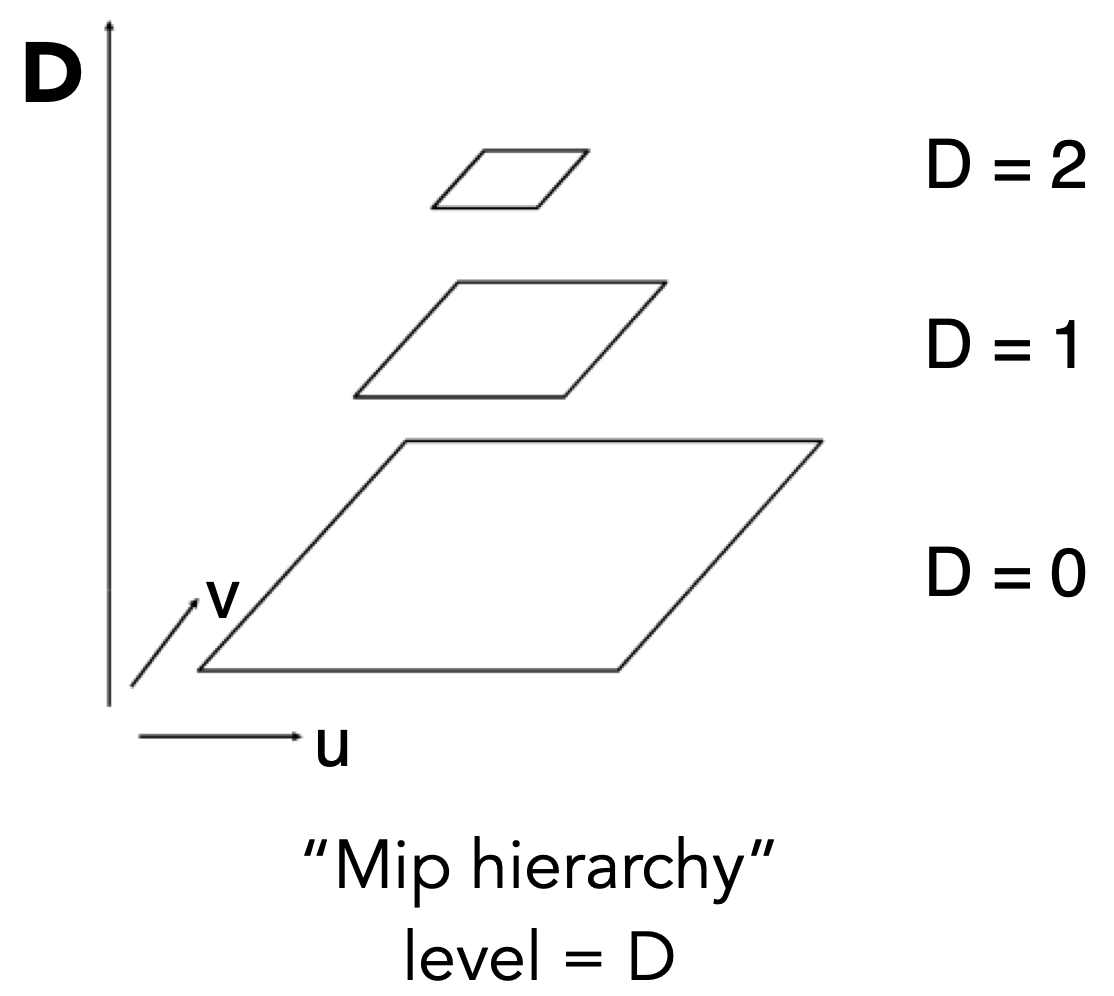
截屏2023-04-13 20.53.07

What is the storage overhead of a mipmap?
- 原图存储量为1，而后每提高一个Level，存储量都变为前者的四分之一
- $1+\frac 1 4++\frac 1 {16}+\frac 1 {64} + … = \frac 4 3$ 即变为原来的三分之四

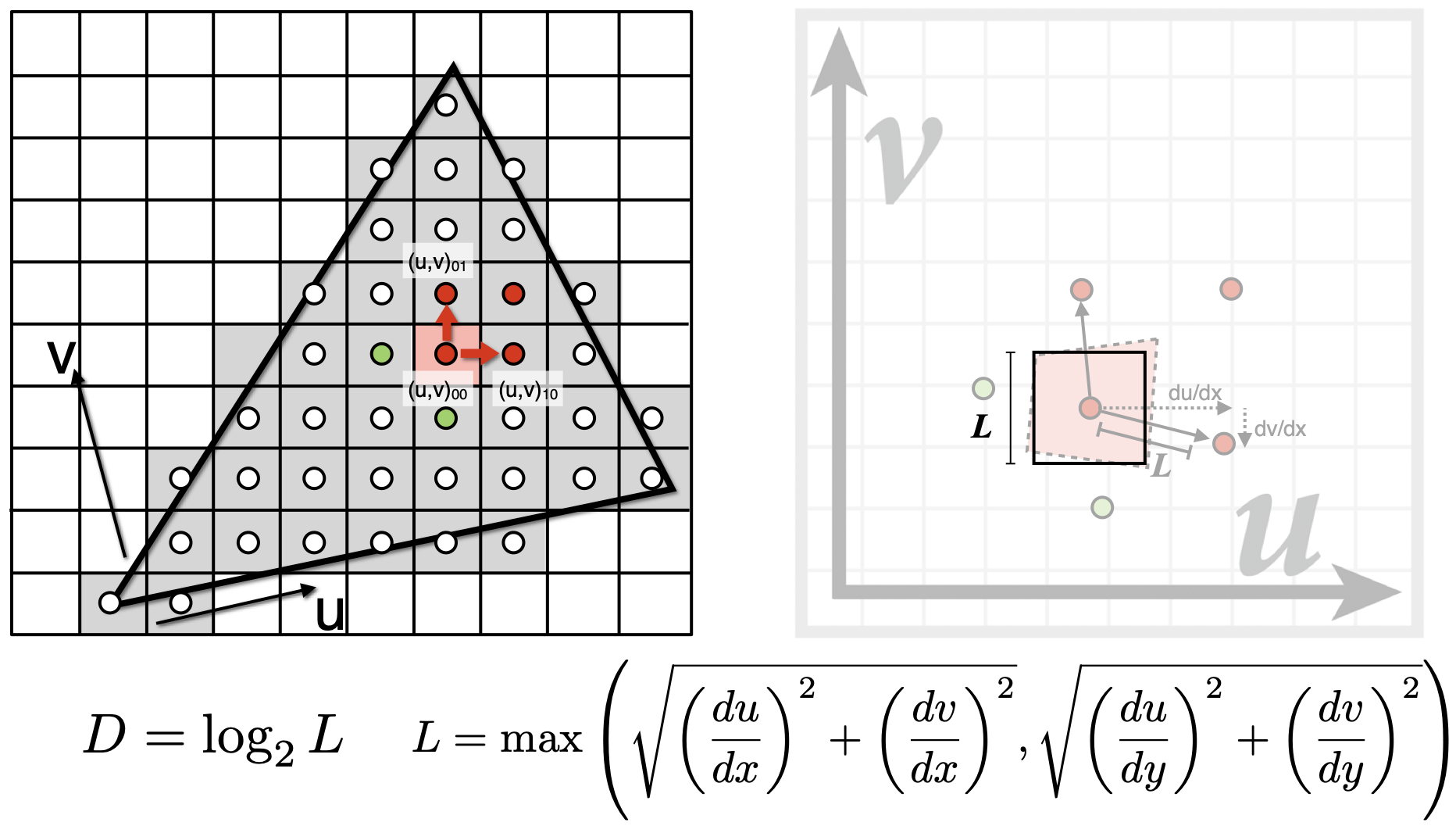
如何计算Mipmap的Level D(得出范围查询的面积)

思路
- 计算一个像素在纹理上的覆盖面积，$D=log_2L$
- 求出这个像素对应的纹理在第几Level会变到一个像素内
- 查找（提前算出Mipmap）对应Level的Mipmap，得出平均值
将像素分别映射到纹理
计算映射到纹理后，各个像素间的距离，$L$取距离的最大值。用正方形近似不规则四边形
得出$D=log_2L$，在根据预先计算好的Mipmap进行对应D的范围查询
- 举例：假如$L$为4（正方形$4 \times 4$），则该区域在$D=2$时，会变为一个像素（正方形$1 \times 1$）
结果
- 问题：渐变不连续，D不为整数时接缝明显
- 解决：Trilinear Interpolation进行过渡

Mipmap间过渡: Trilinear Interpolation 三线形插值

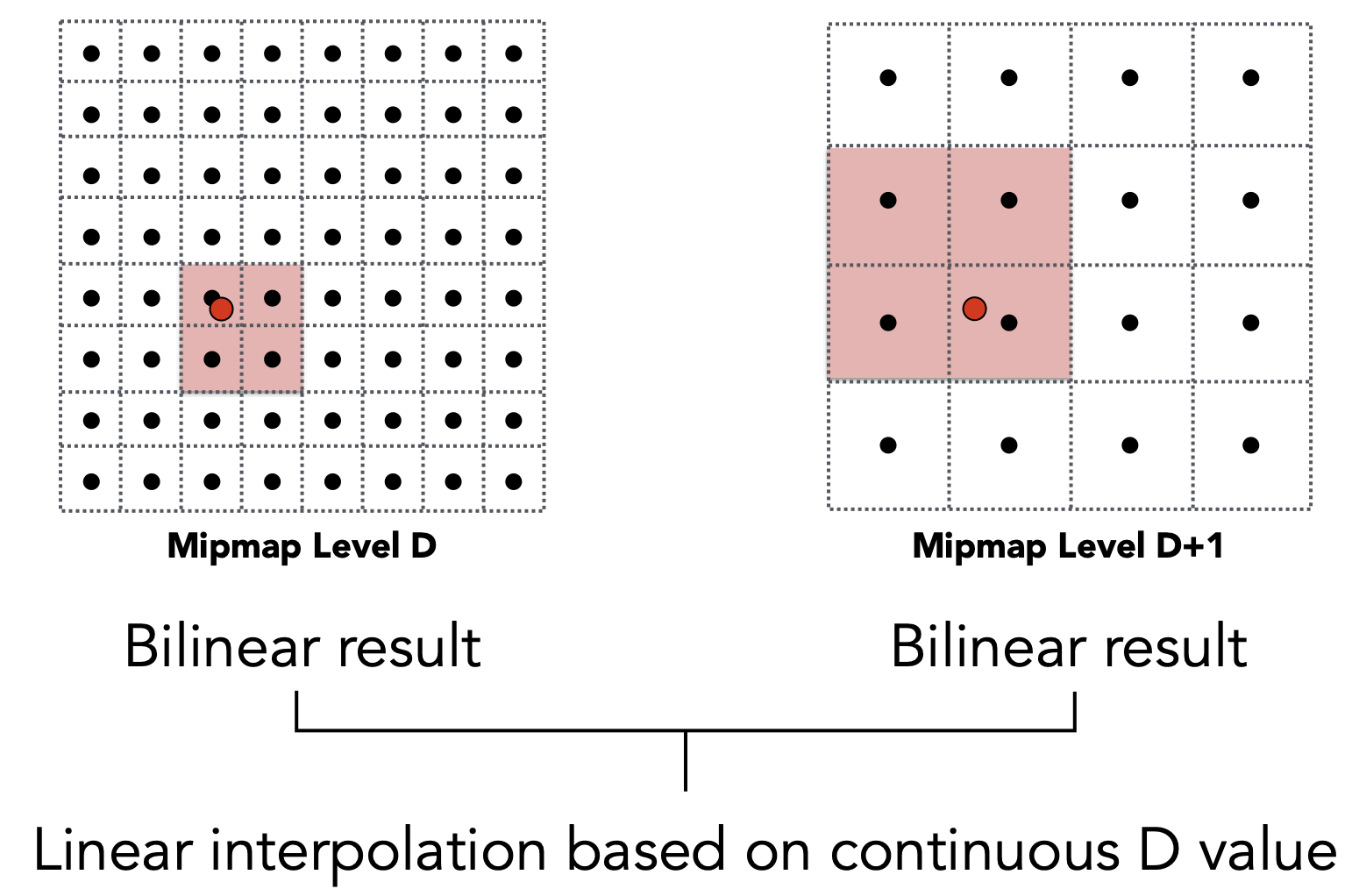
- 两层Level分别先做Bilinear Interpolation，所得的插值结果再进行一次插值
结果
三线形插值优点
- 得到完全连续的过渡
- 开销小：做两次查询，一次插值
三线形插值的局限性：远处overblur

Anisotropic Filtering各向异性过滤；EWA Fliter

解决
各向异性过滤可解决mipmap只能查询正方形的问题。（可对单一方向压缩剧烈的长条形区域进行范围查询，不必限制在正方形内）
但是各向异性查询对如下对角线方向倾斜的矩形仍无法完美近似，因此也存在局限性
解决：EWA filtering

Application of texture

纹理应用范围很广

Environment Map 环境光贴图

运用环境光贴图的假设前提：光来自无限远处，贴图只记录方向信息，无实际深度意义
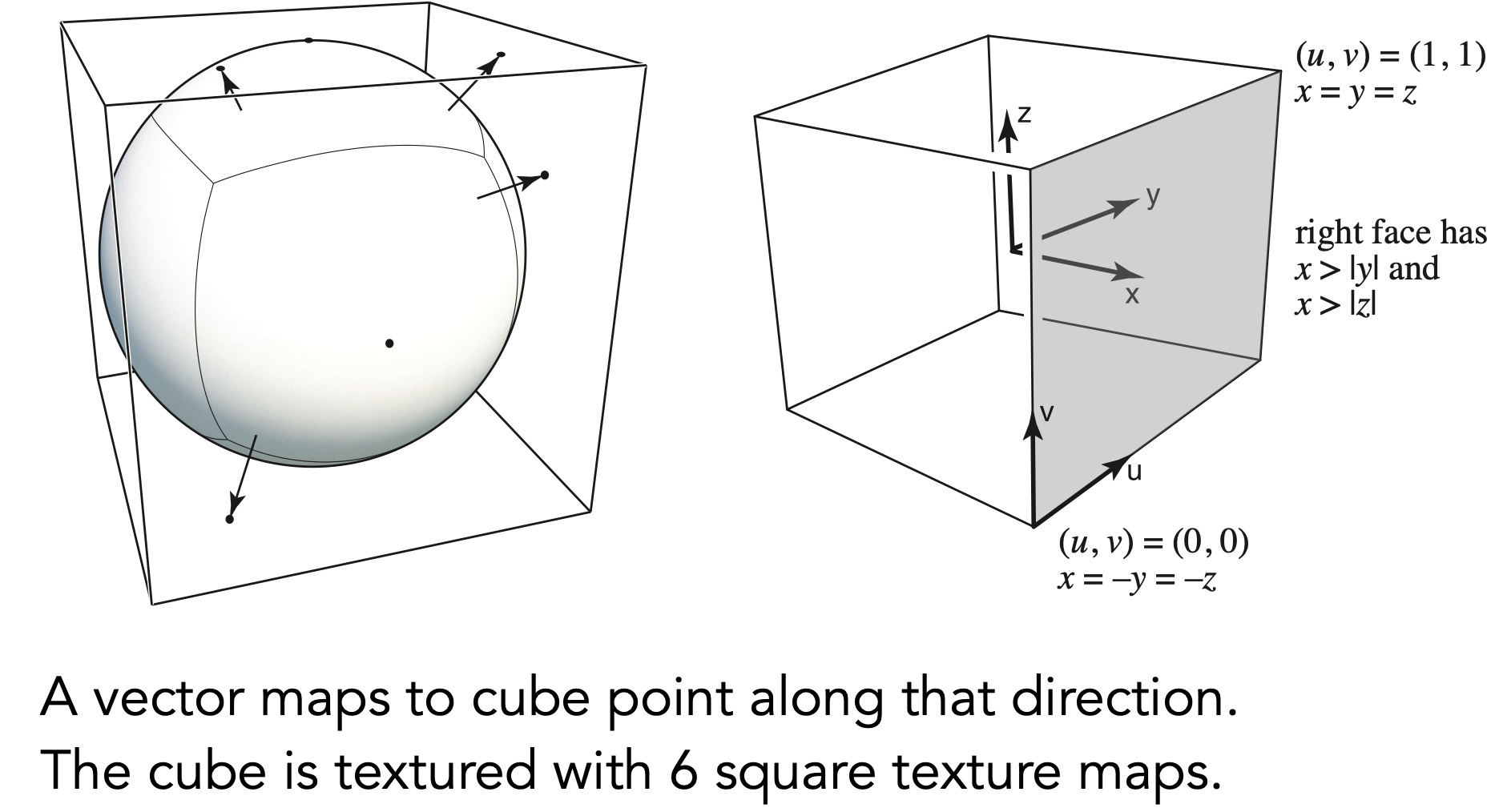
Spherical Environment Map
- 环境光贴图被记录在球面上
- 展开会产生扭曲，无法均匀描述
利用 Cube Map 解决扭曲问题

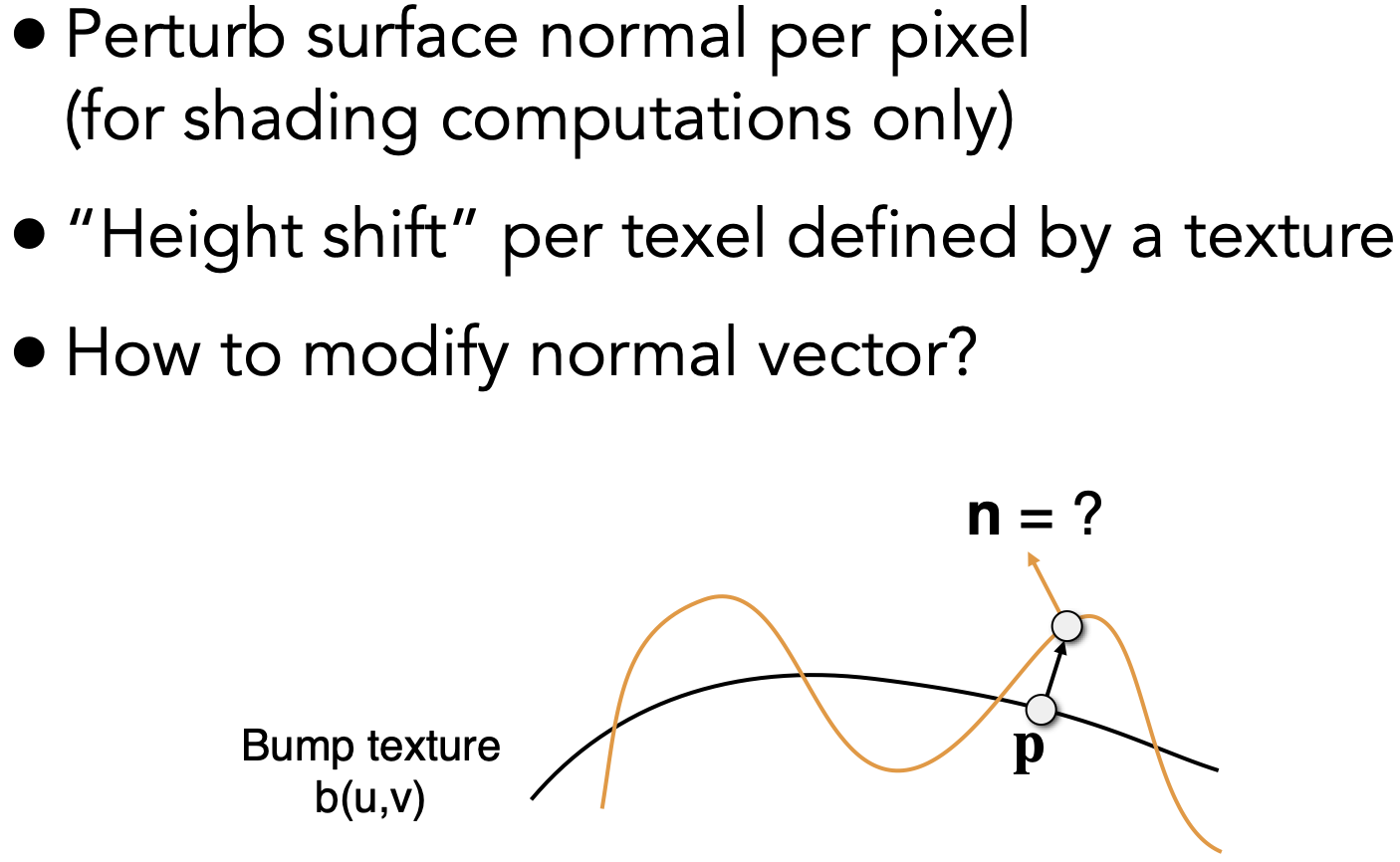
Bump Map 凹凸贴图

区分：高度贴图和法线贴图
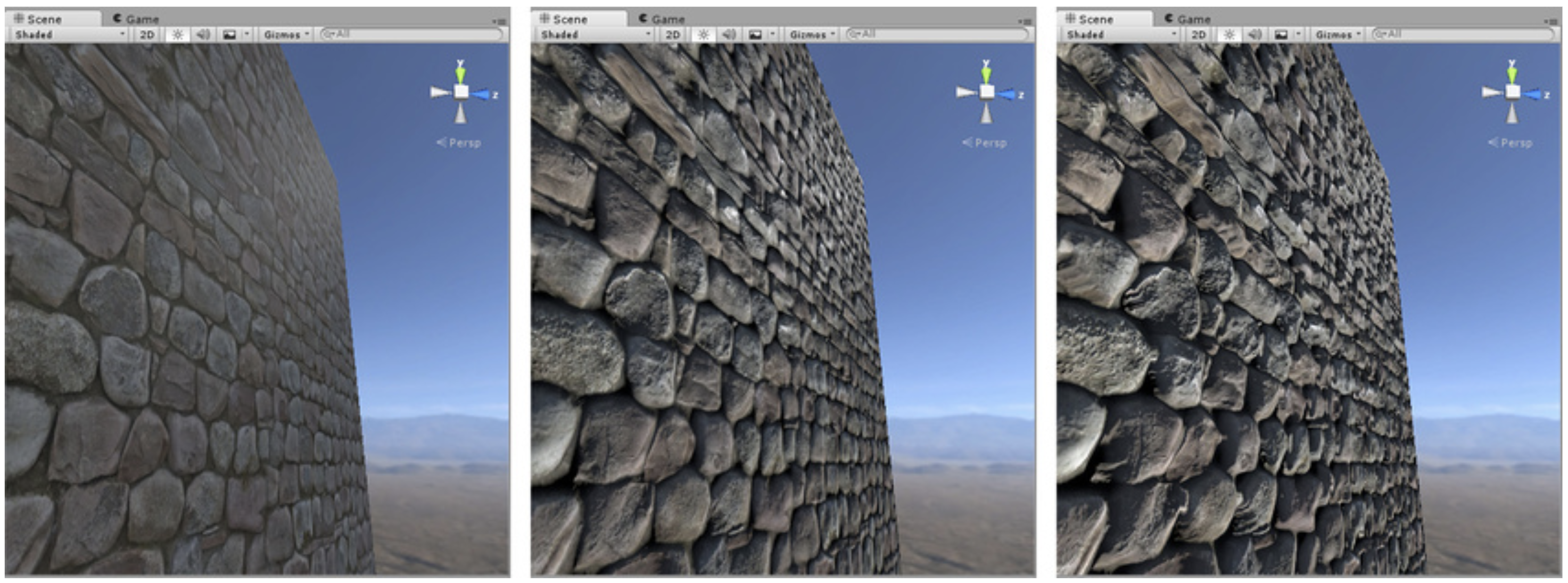
- - 1. base color
    2. base color + normal：法线贴图修改表面光照
    3. base color + normal + height：高度贴图实现遮挡
Height map: 定义在法线基础上，上下位移的相对高度
作用
- 在不增加三角面的基础上，增加表面细节
法线的计算
- Case1: flatland 图中原本面为平面，蓝色面由凹凸贴图定义得到：
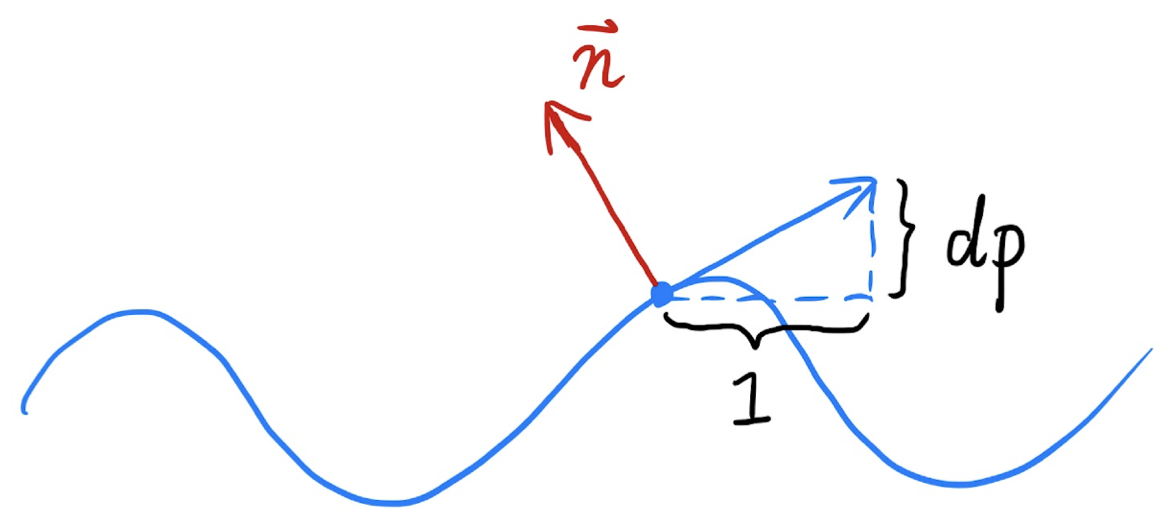
  - 思路：
    1. 平面上$p$点原本法线：$n(p) = (0,1)$
    2. 应用凹凸贴图后，$p$点切线方向：$dp = c*[h(p+1) - h(p)]$ (其中$c$为常数，用于表示凹凸贴图的影像大小)
    3. 由于法线垂直于切线，即可知：$n(p) = (-dp, 1).normalized()$
- Case2: 3D
  - 思路：
    - 原平面表面法线：$n(p) = (0,0,1)$
    - 对贴图在三维空间的$u$方向和$v$方向求偏导：
      - $dp/du = c1 * [h(u+1) - h(u)]$
      - $dp/dv = c2 * [h(v+1) - h(v)]$
    - 得出切线方向：$n(p) = (-dp/du, -dp/dv, 1).normalized()$
  - 注意⚠️：以上计算均在切线空间、局部空间进行（记得去补这块内容！！）
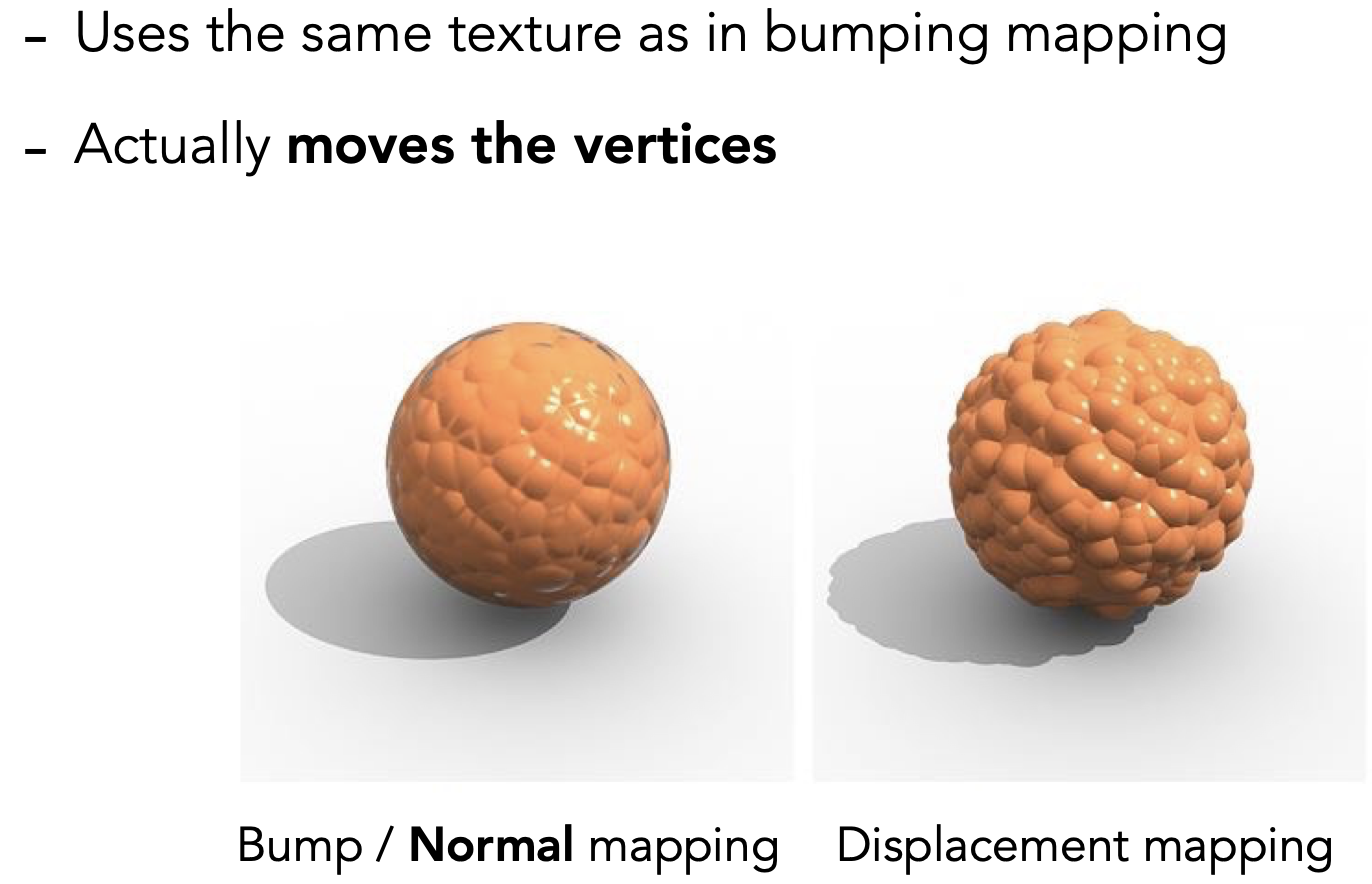
Displacement Map 置换贴图
- 对顶点进行真实的位移
- 区分：bump vs. normal vs. displacement
- 代价：三角面数需足够多，需高于置换贴图的采样频率
  - 理想：根据置换贴图采样频率，按需规定模型细分精度
  - DX中解决方法：动态曲面细分Dynamic Tessellation

三维纹理

3D Procedural Noise + Solid Modeling
- 纹理是实心的球，可以定义三维空间中任意一点的纹理。
- 并没有生成对应的内部纹理图，但是定义了一个三维空间中的噪声函数(Perlin Noise)，可以通过解析式算出任意一点的噪声

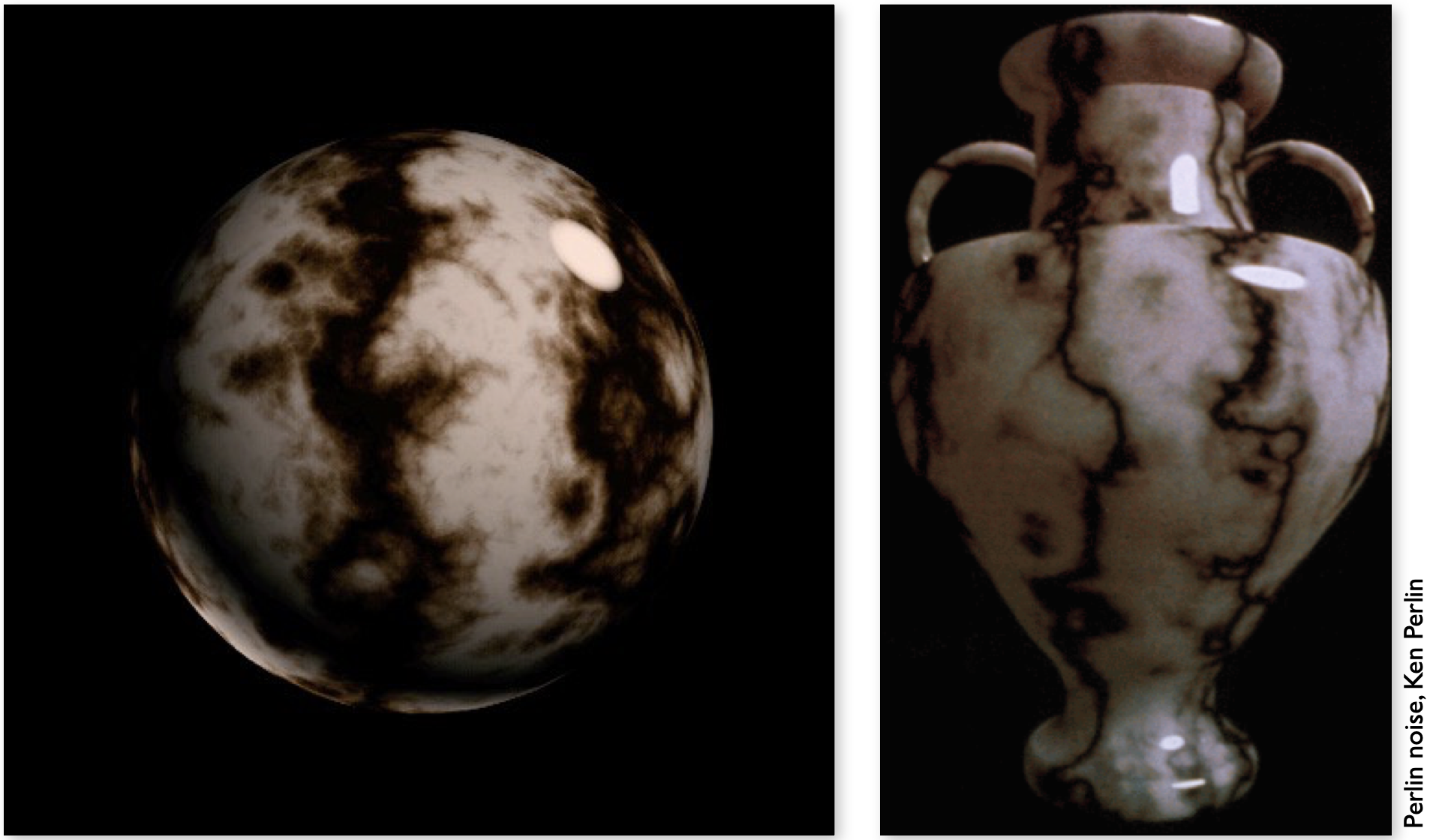
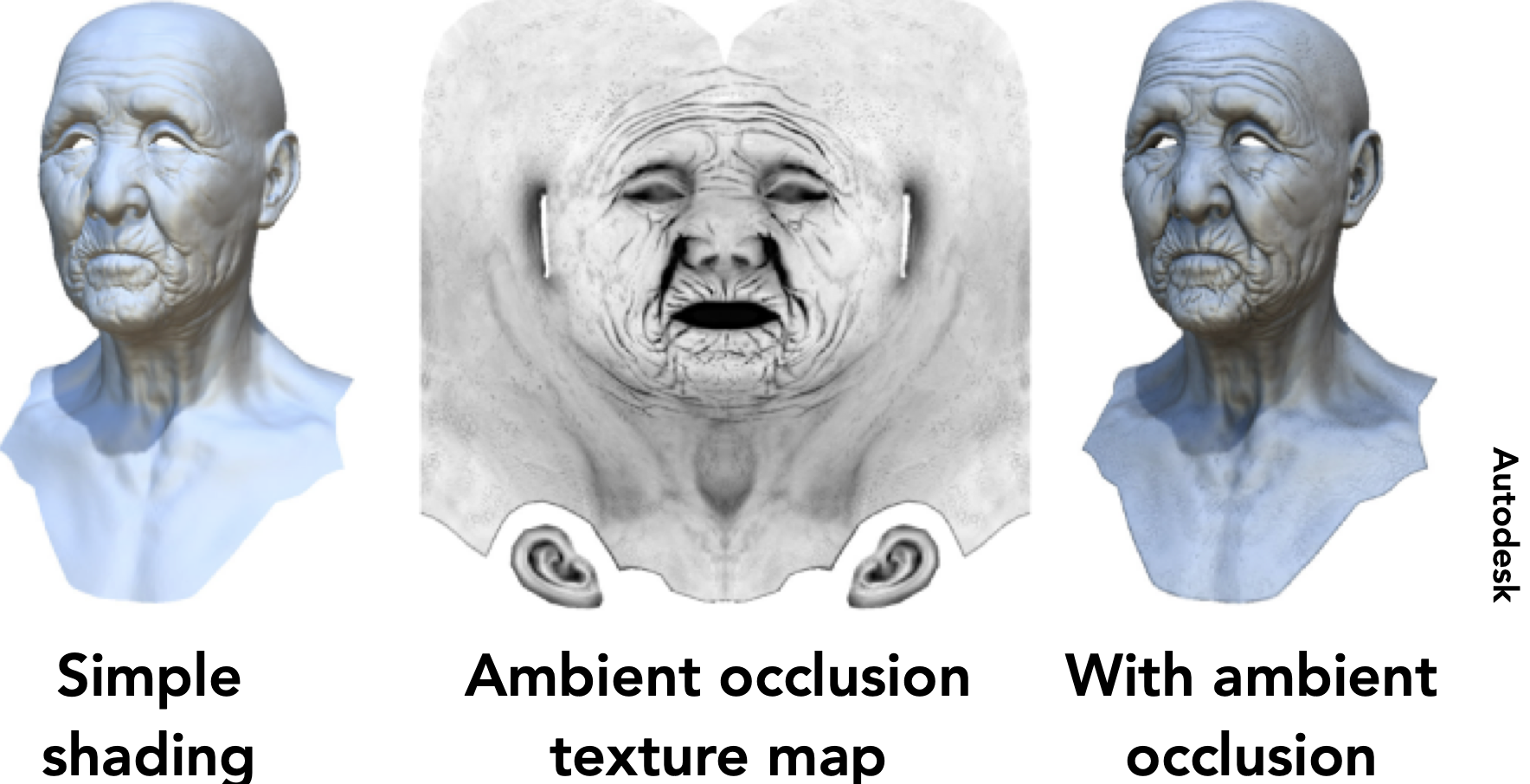
Provide Precomputed(预先计算的) Shading

eg：提前计算AO Map，与原有shader做multiple

截屏2023-04-15 00.44.30

3D Textures and Volume Rendering

eg：医学CT影像，扫描出的数据处理成三维纹理以呈现

截屏2023-04-15 00.49.03

P7 Shading (Illumination, Shading and Graphics Pipeline)

Shading Definition

简单的着色例子：Blinn - Phong Reflection Model

Shading in Local

Diffuse Reflection 漫反射

P8 Shading (Pipeline and Texture Mapping)

Blinn - Phong Model

Specular Term 高光

Ambient Term 环境光

最终效果

Shading Frequencies 着色频率

Flat Shading: shade each triangle

Gouraud Shading: shade each vertex

Phong Shading: shade each pixel

对比

定义顶点法线方向

定义像素法线方向

Graphics (Real-time Rendering) Pipeline 实时渲染 渲染管线

渲染管线概述

Shader Programs

Texture Mapping 纹理映射

P9 Shading (Texture Mapping cont.)

Interpolation Across Triangles: Barycentric Coordinates 重心坐标

Applying Textures 纹理应用

Texture Magnification(纹理分辨率小，需放大)

Nearest

Bilinear Interpolation 双线性插值

Bicubic Interpolation

Texture Magnification(纹理分辨率大，需缩小)

Mipmap: Allowing (fast, approx., square) range queries

Intro

如何计算Mipmap的Level D(得出范围查询的面积)

Mipmap间过渡: Trilinear Interpolation 三线形插值

Anisotropic Filtering各向异性过滤；EWA Fliter

Application of texture

Environment Map 环境光贴图

Bump Map 凹凸贴图

三维纹理

Provide Precomputed(预先计算的) Shading

3D Textures and Volume Rendering

Graphics (Real-time Rendering) Pipeline 实时渲染渲染管线