Games101-P10-12 Geometry
- P10&11 Preview
- Introduce to geometry
- Examples of geometry
- Various representations of geometry
- Implicit
- Explicit
- Introduce to geometry
P11 Preview
Curves
- Bézier Curves
- De Casteljau’s algorithm
- B-splines, etc.
Surfaces
- Bezier surfaces
- Triangles & quads
- Subdivision, simplification, regularization
P12 Preview
- Mesh Subdivision (upsampling)
- Mesh Simplification (downsampling)
- Mesh Regularization (same #triangles)
P10&11 Geometry (Implicit&Explicit)
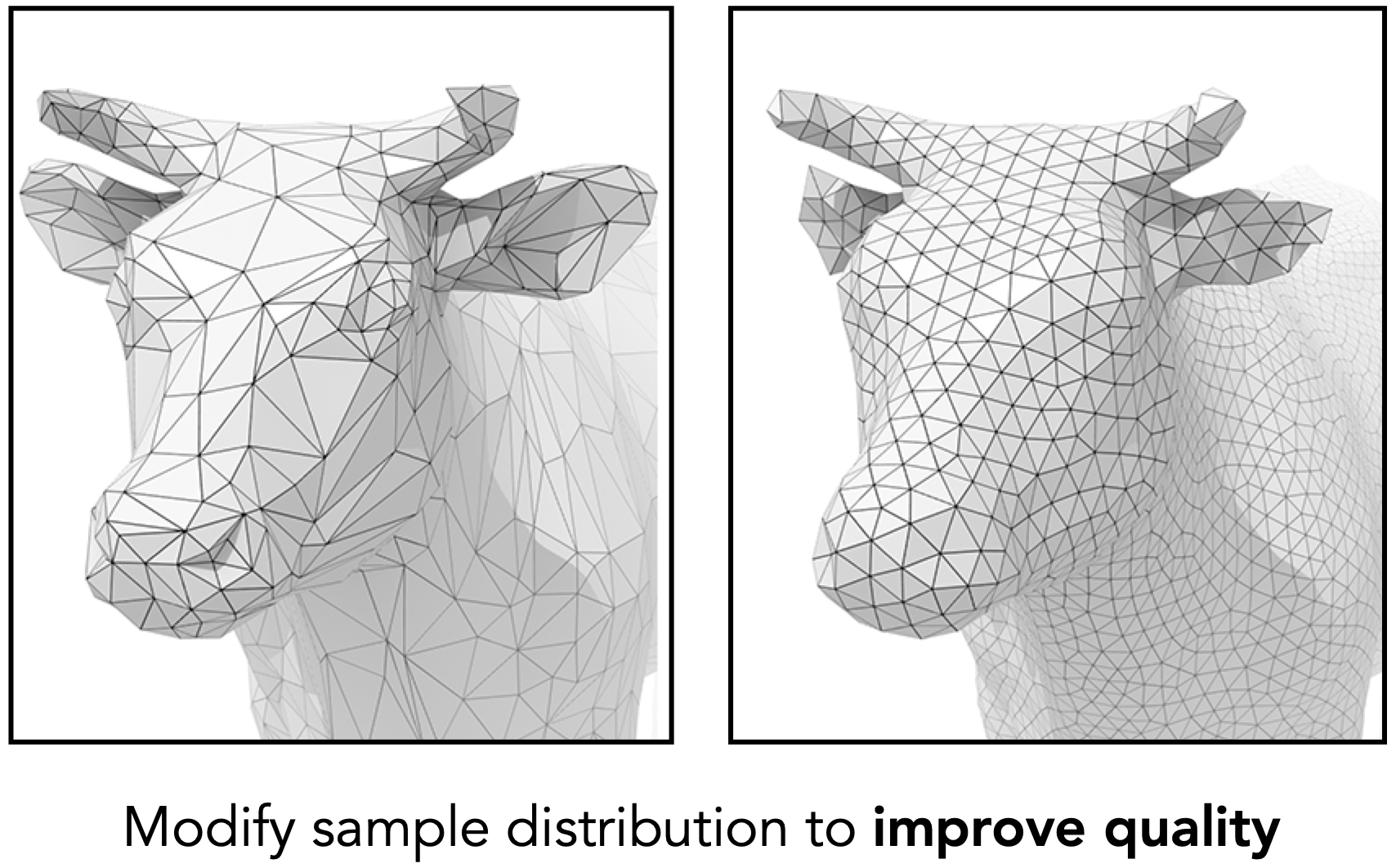
- 难点:存储;渲染
- 过于精细不适宜三角面表示
几何的表示形式
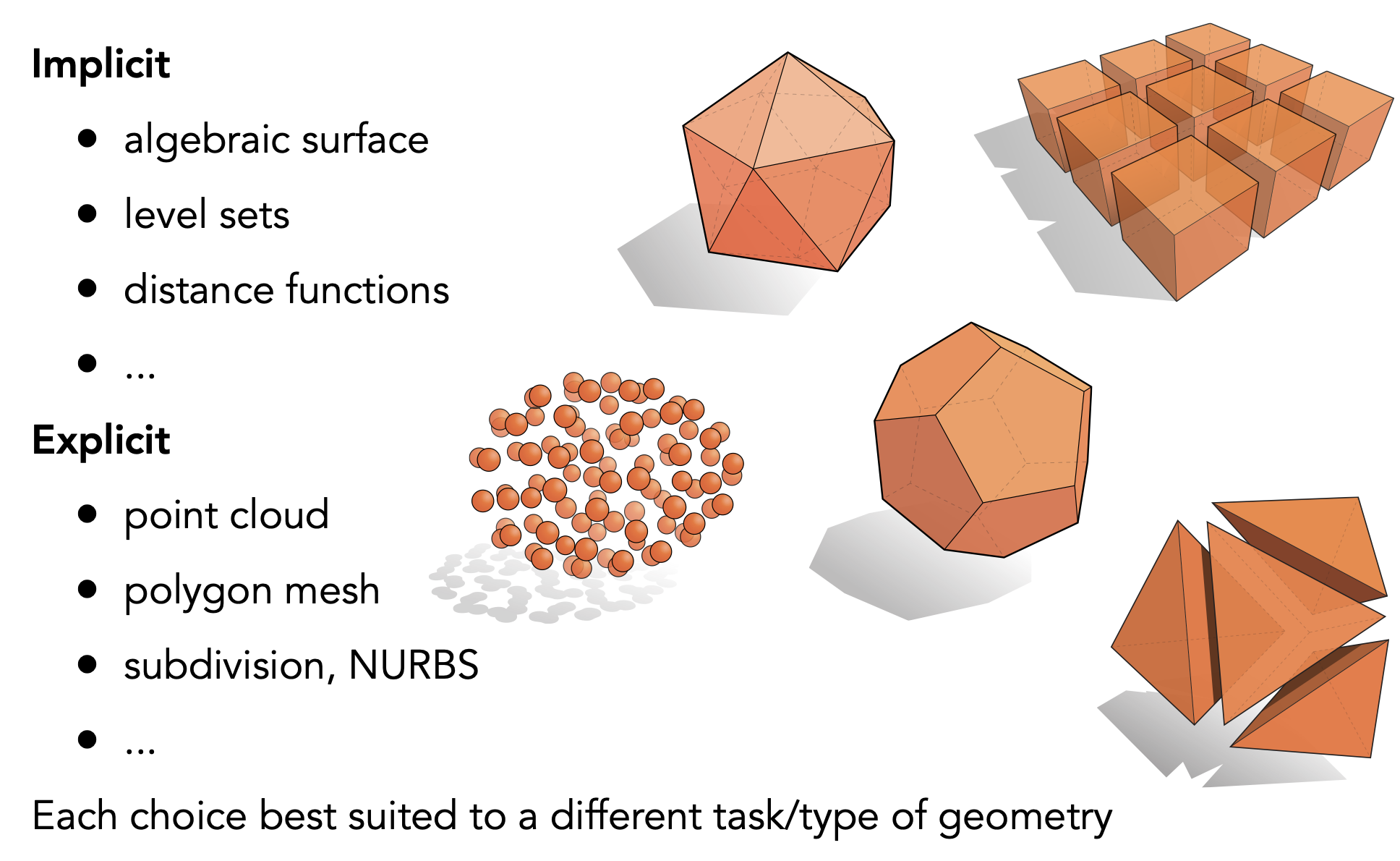
几何的隐式(Implicit)表示
Intro - 隐式函数
- 已知几何的点满足一定关系,未知点的具体位置
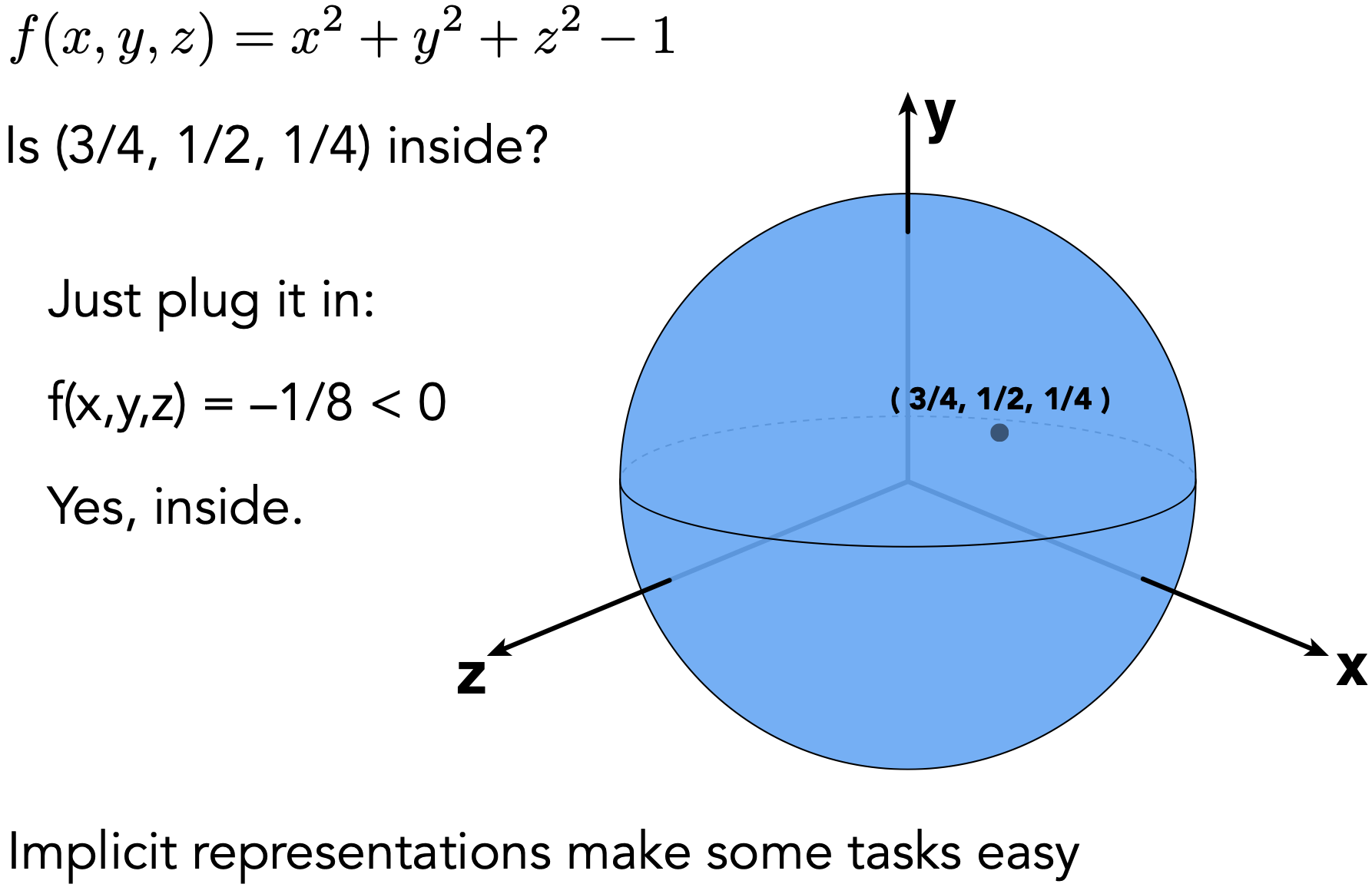
- eg:三维空间中单位球 $x^2+y^2+z^2=1$
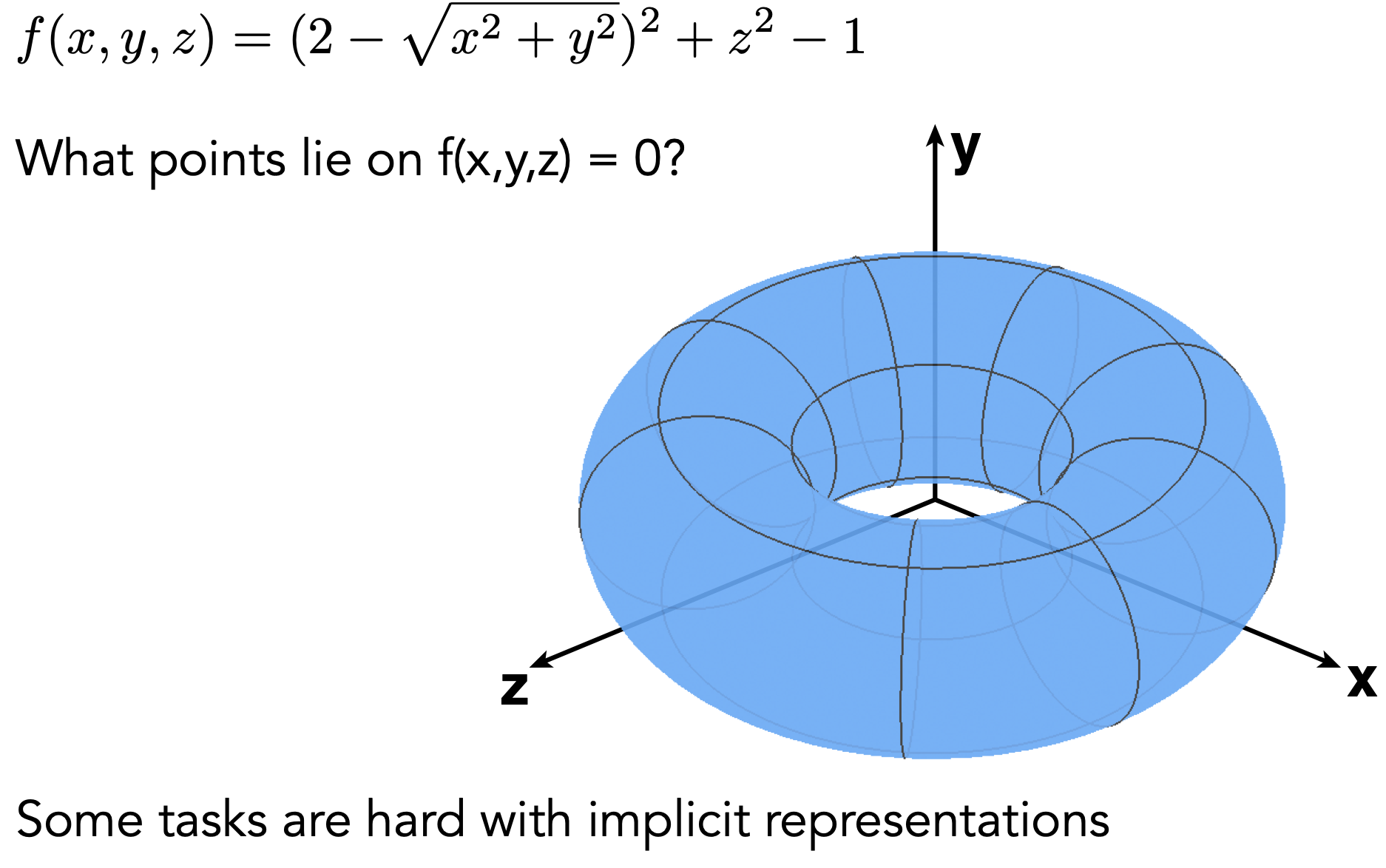
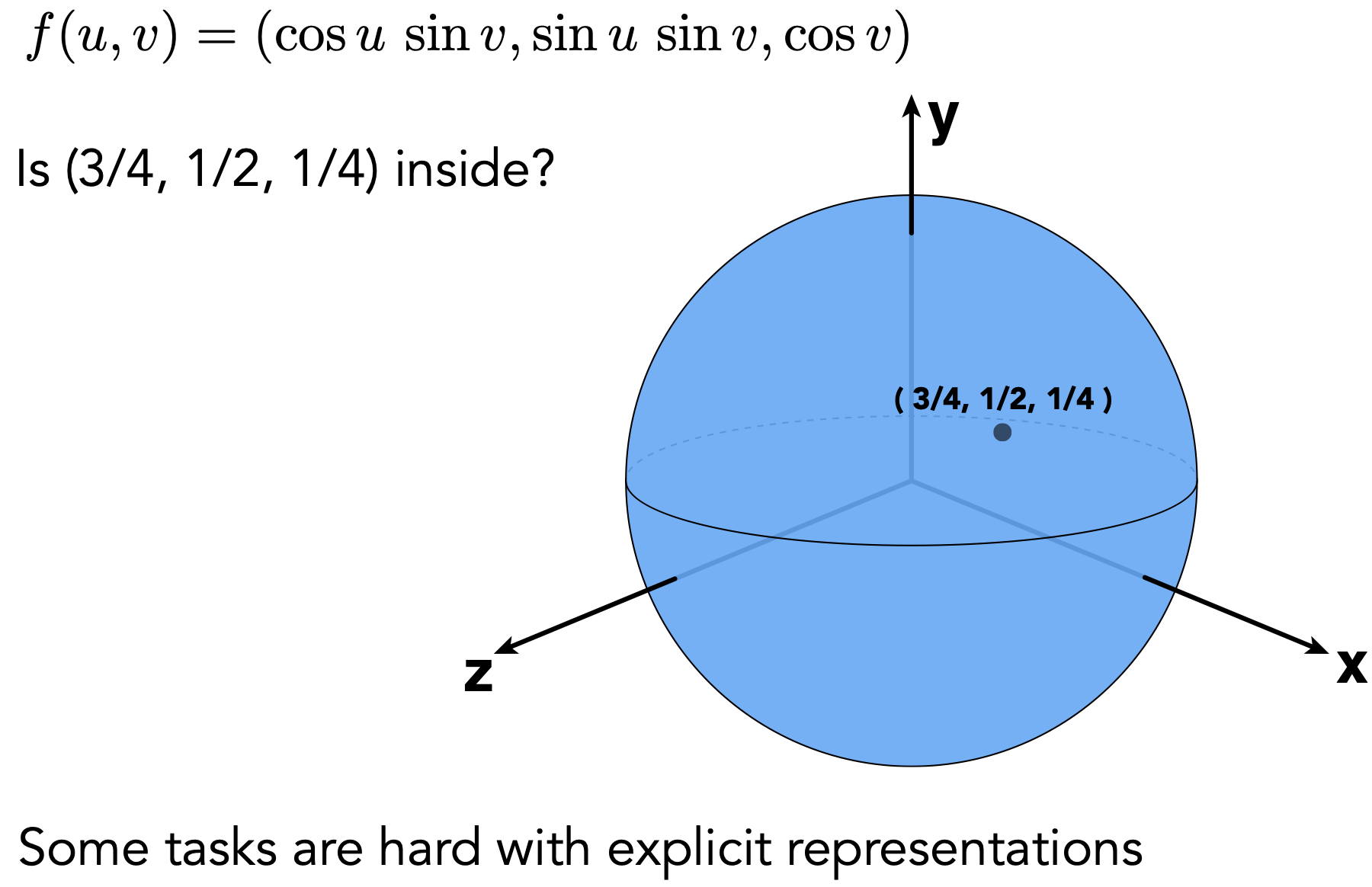
- 通用:$f(x,y,z) = 0$
- 缺点:采样难,所表现的形状不直观
- 优点:便于检测点是否在物体表面上/内/外
Algebraic Surfaces
- 可表述参数化模型,而无法表述复杂的又不可参数化描述的模型
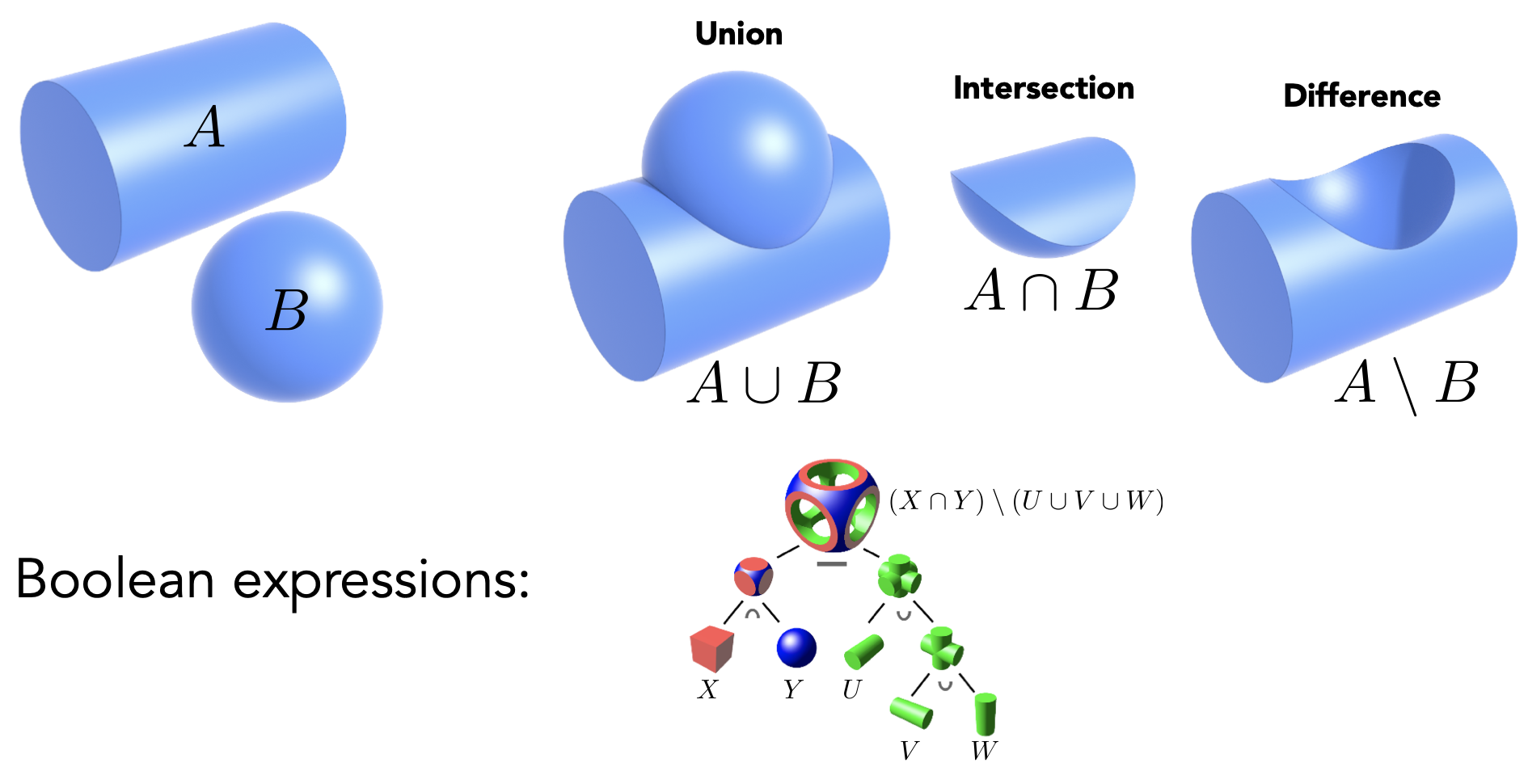
Constructive Solid Geometry
- 通过一系列基本几何的布尔运算,来定义新的几何
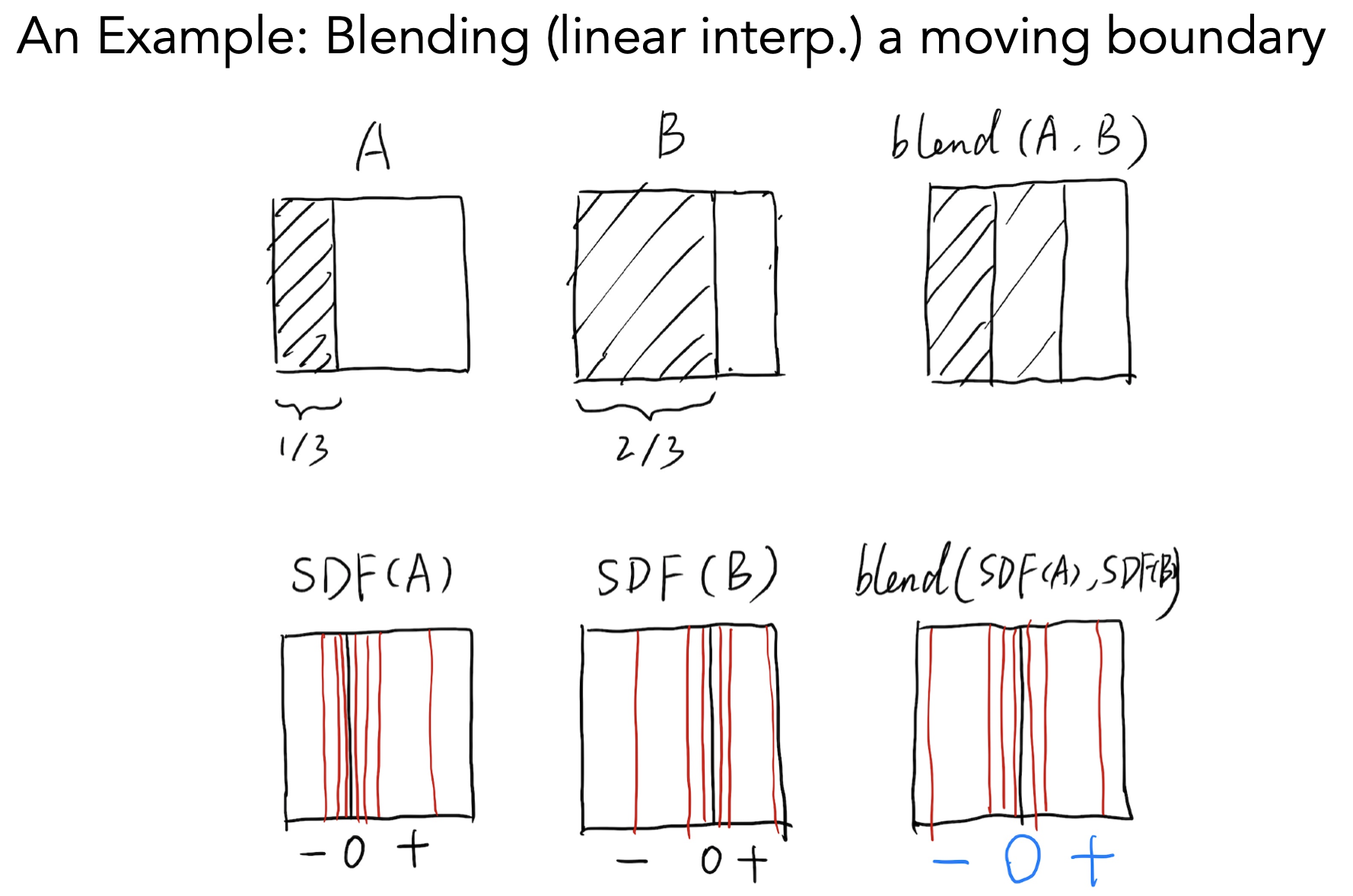
Distance Functions
- 距离函数:对空间中任何一个点,到想要的几何形体表面的最小距离(内负外正)。将两个物体的空间函数blend后,推算出得到的新的函数所表示的几何形体
- 理想:blend后得到二者位置的中间状态,SDF为0处表示物体边缘
- 大神作品:https://iquilezles.org/www/articles/raymarchingdf/raymarchingdf.htm
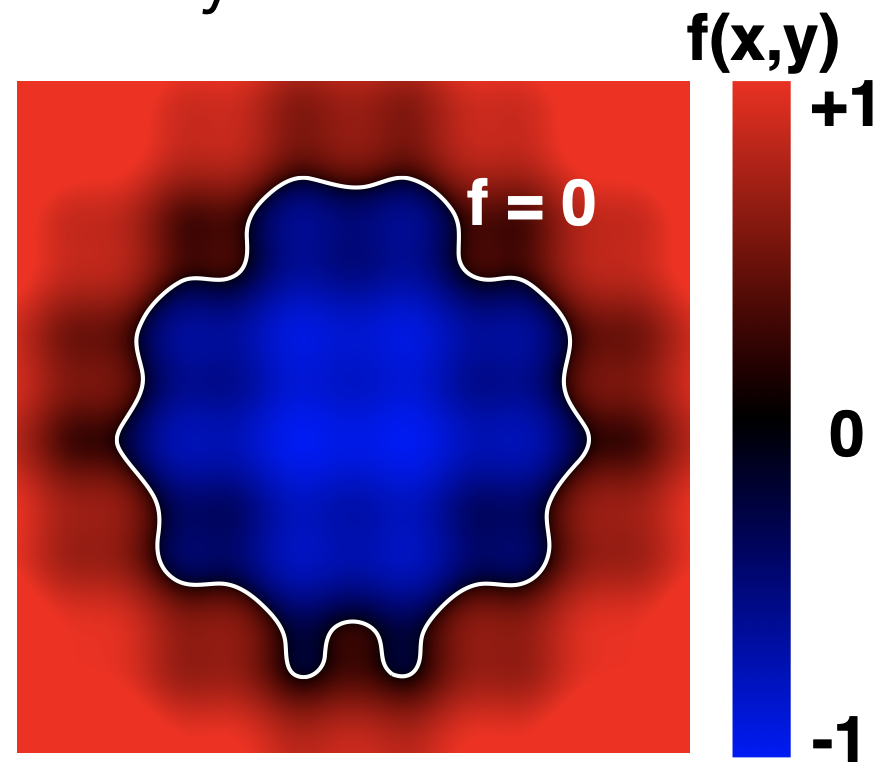
Level Set Methods 水平集
与距离函数类似,只是表示形式不同
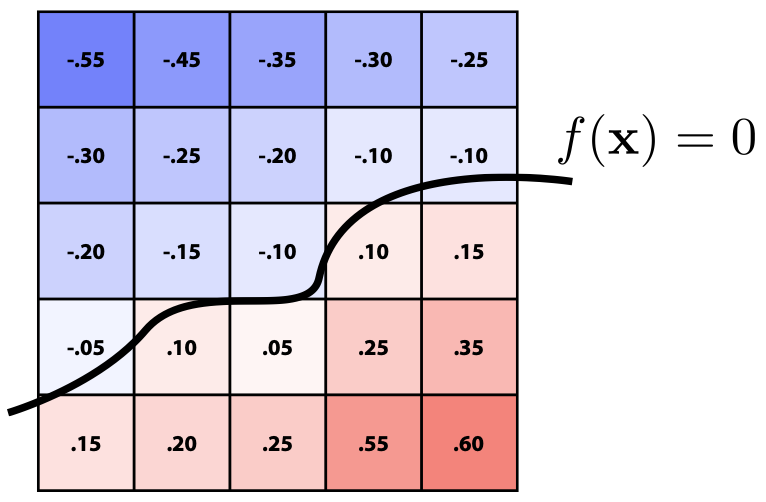
封闭形式的方程很难描述复杂的形状
替代方案:存储一个近似函数的值网格
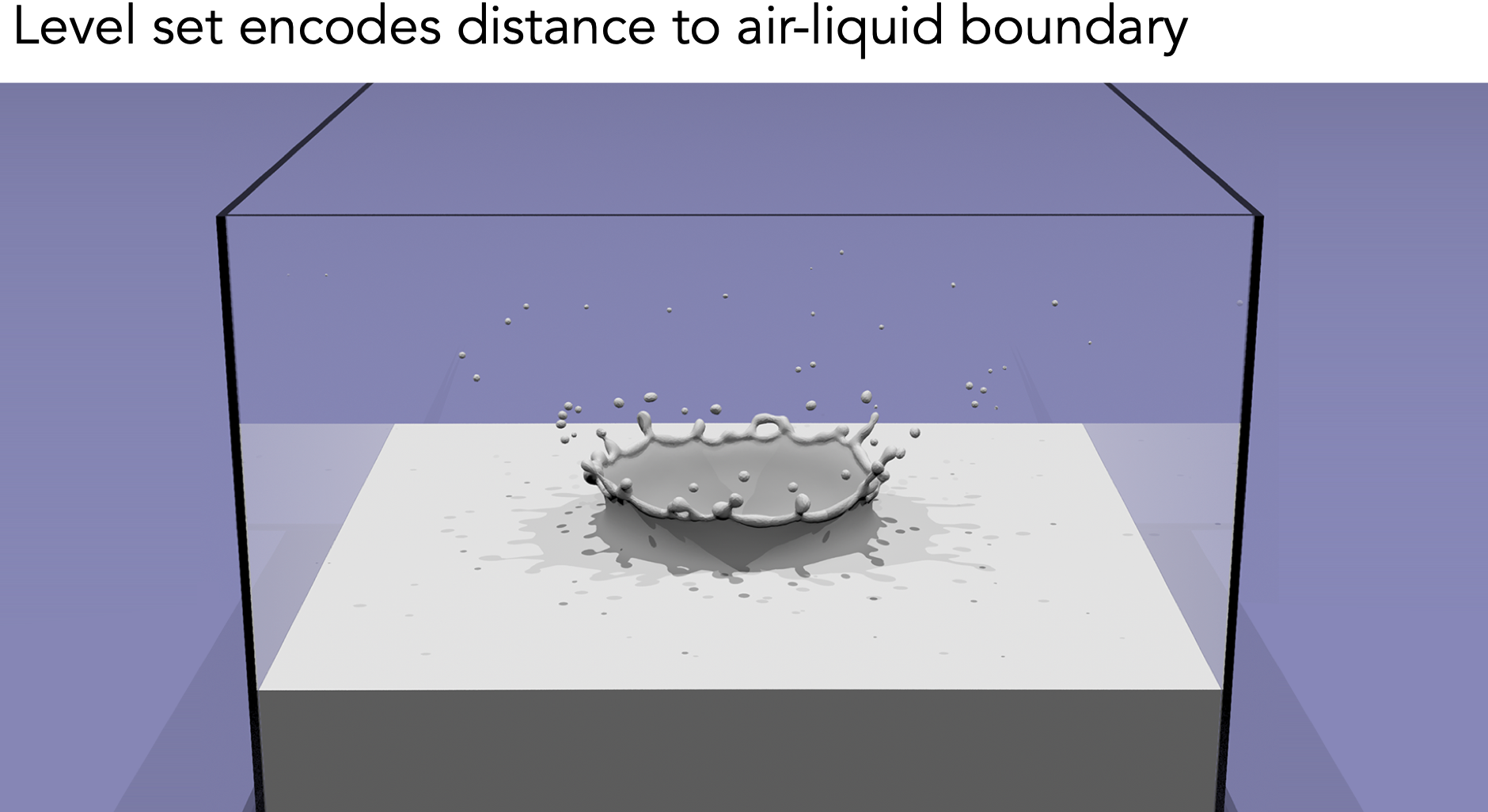
表面处,值为0
提供对形状的更明确的控制(如纹理)
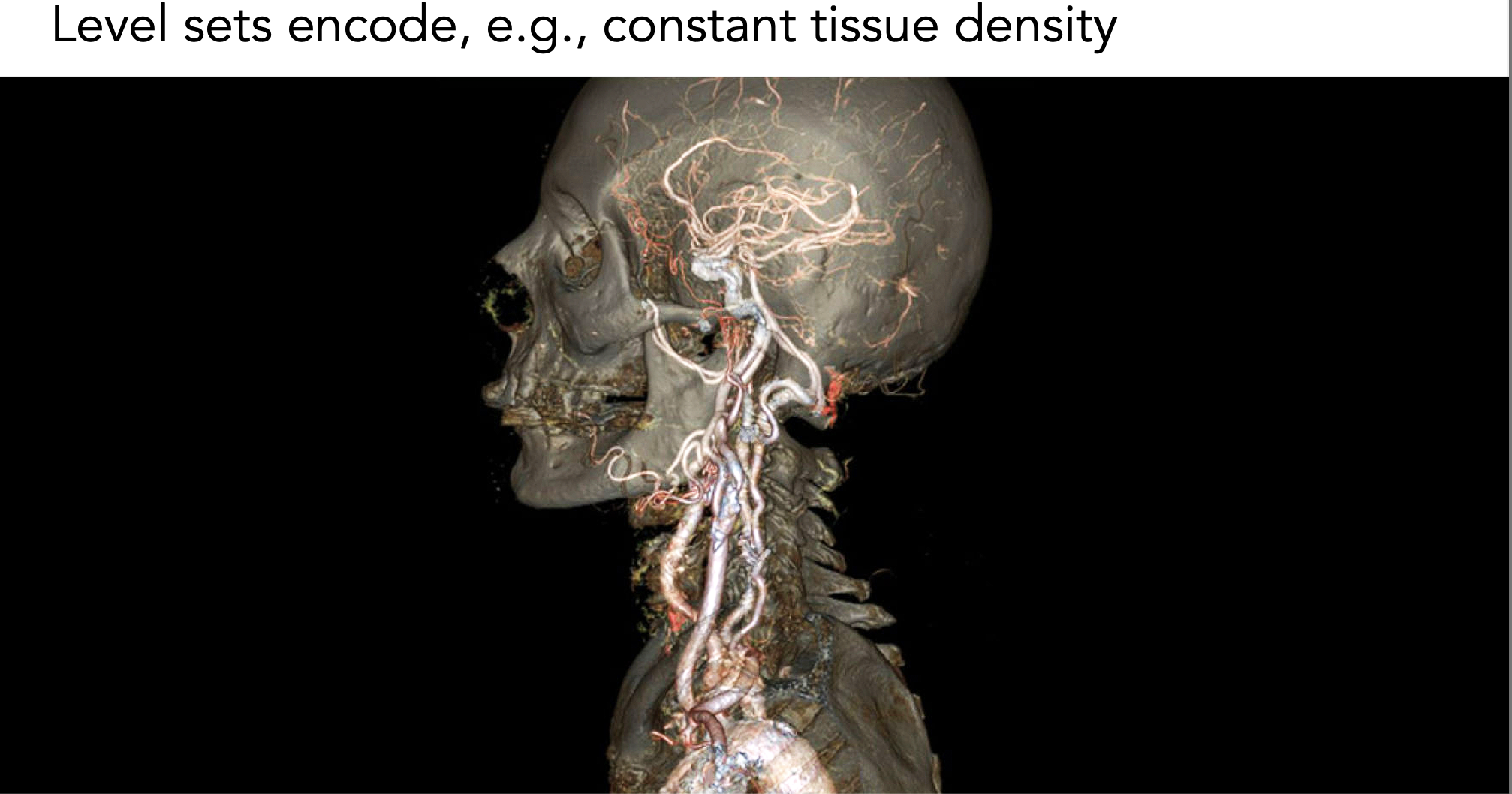
水平集的三维应用
- Level Sets from Medical Data
- Level Sets in Physical Simulation,如水滴融合
- Level Sets from Medical Data
Fractals 分形
- 自相似,理解为递归
Pros & Cons 隐式表示利弊分析
- Pros
- 函数描述几何形体,紧凑
- 容易查询,如inside object, distance to surface
- good for ray-to-surface intersection
- 对于简单的物体,描述精确,且无采样造成的错误
- 容易处理拓扑结构的变化(例如,流体)
- Cons
- 很难模拟复杂的形状
几何的显式(Explicit)表示
Intro - 显式表示
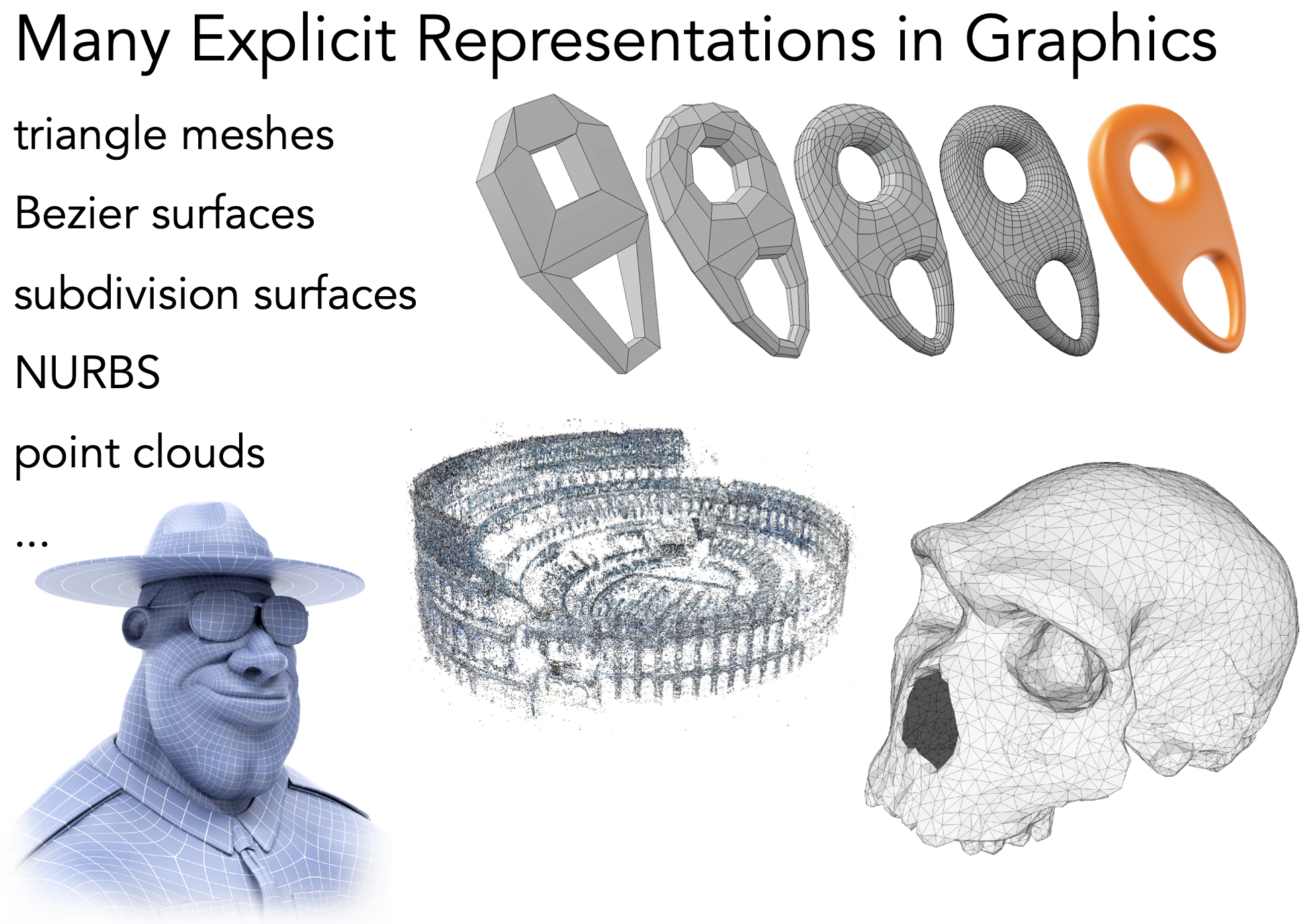
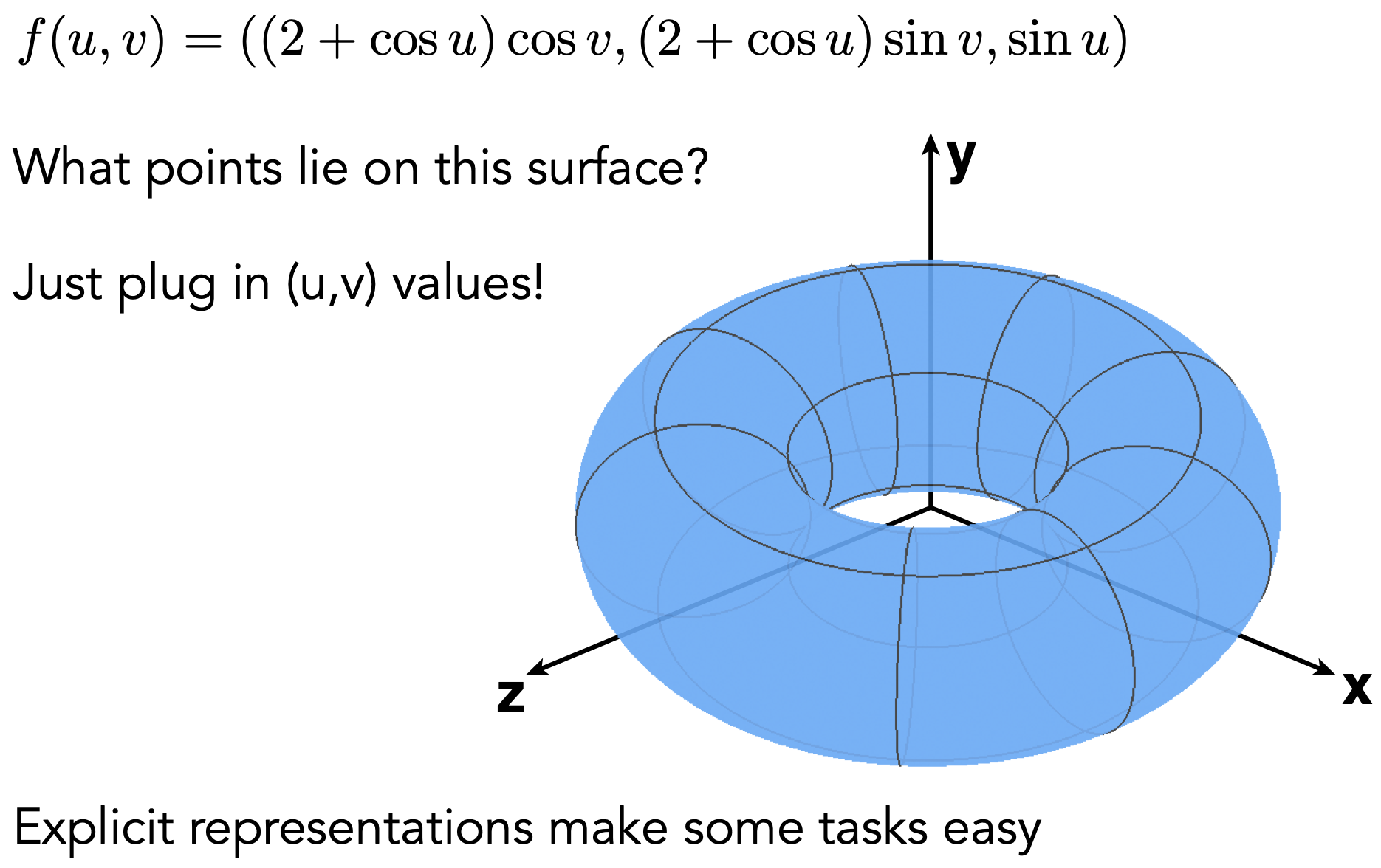
- 所有点直接给出,或通过参数映射
- 给出一个函数$f$,可将$uv$映射到$xyz$
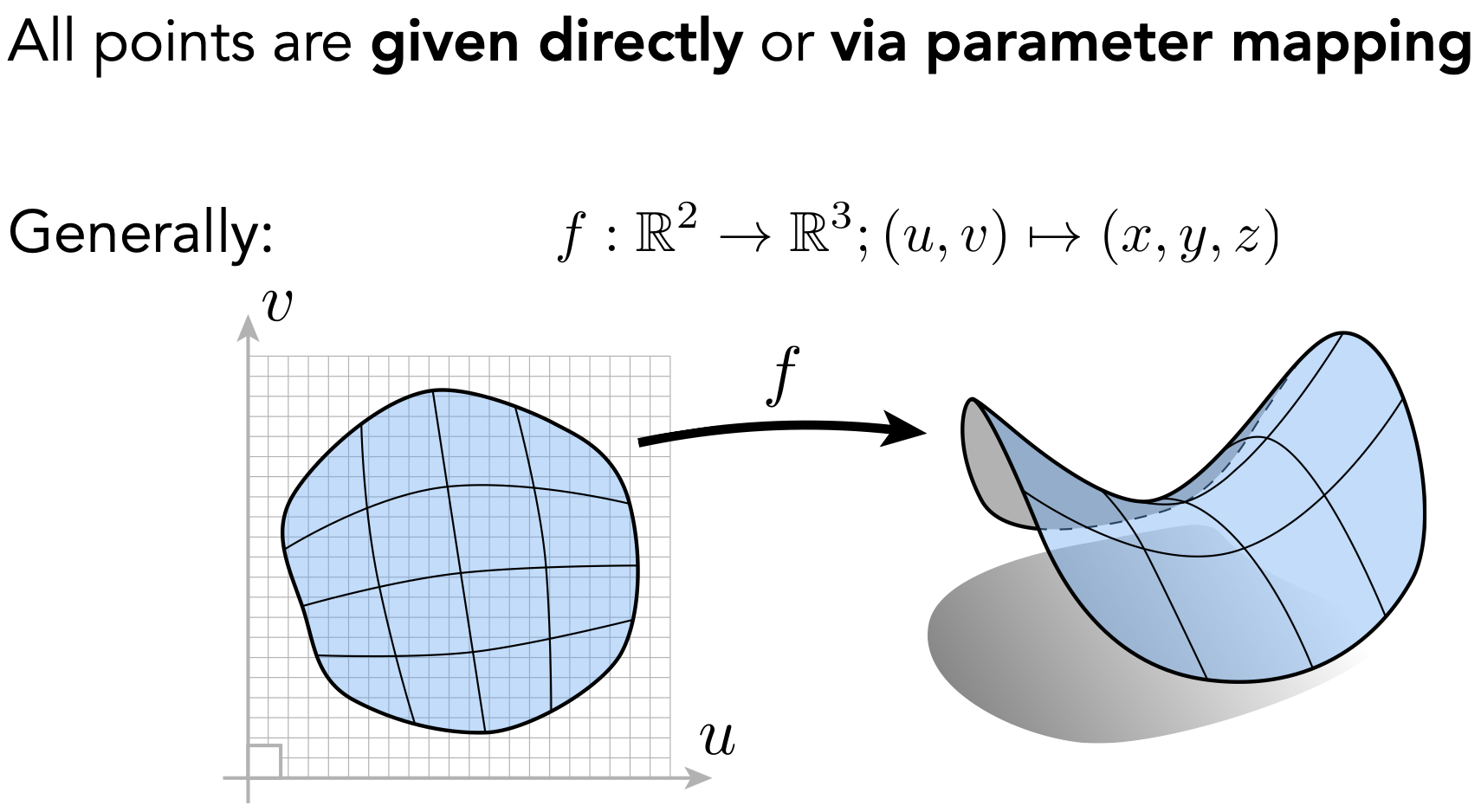
- 优点:采样简单,可直接通过已知的$uv$的出对应的$xyz$
- 缺点:难以判断点是否在物体表面上/内/外
- 按需选择表示方法
Point Cloud 点云
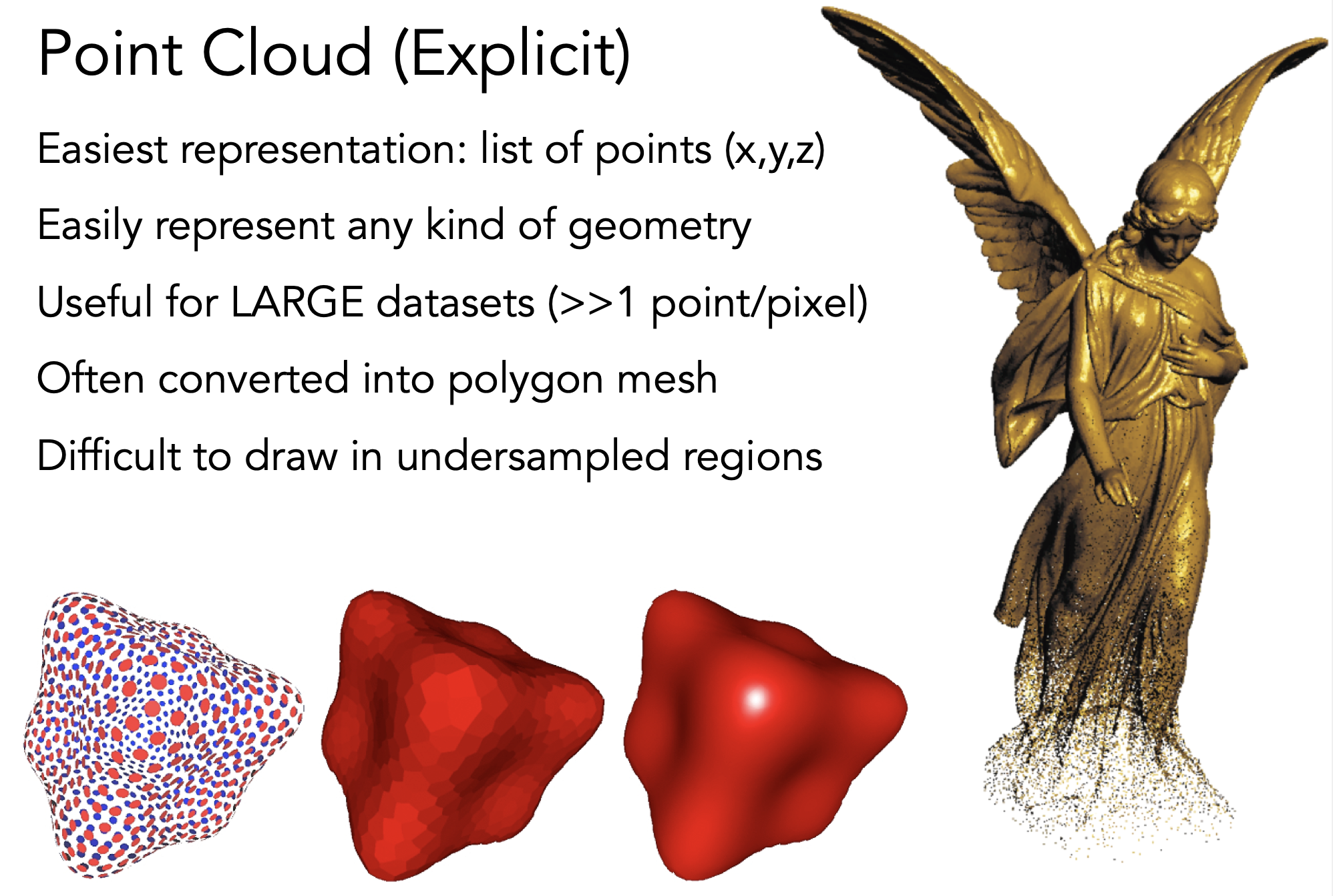
Polygon Mesh

- 如何表示用三角形面形成的物体:The Wavefront Object File (.obj) Format
- 是一种存储vertices, normals, texture, coordinates和它们之间联系的文本文件
- 如图,表示一个立方体的八个点(v点,vn法线,vt纹理坐标,f面联系 v/vt/vn)
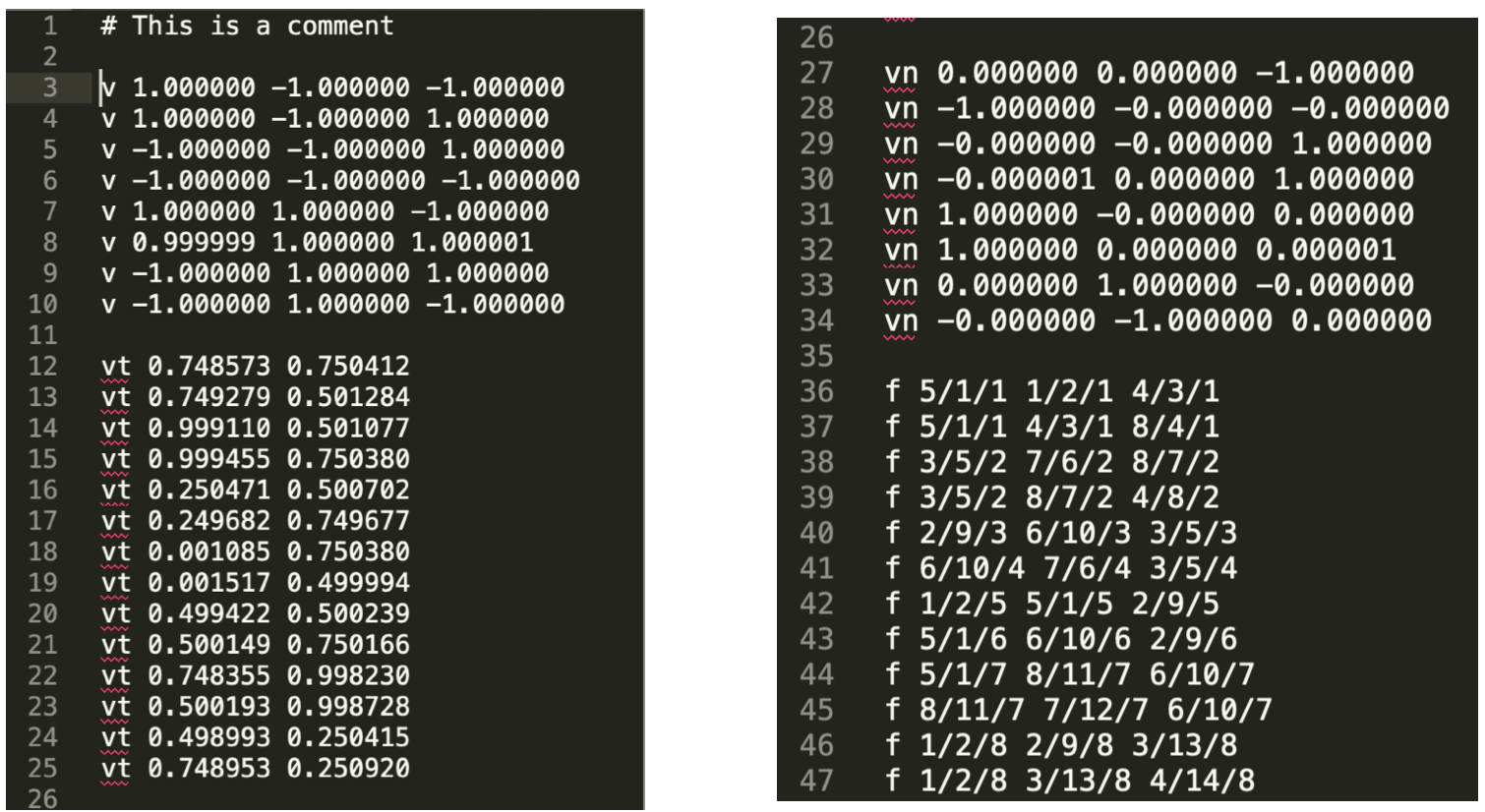
- 如图,表示一个立方体的八个点(v点,vn法线,vt纹理坐标,f面联系 v/vt/vn)
- 是一种存储vertices, normals, texture, coordinates和它们之间联系的文本文件
P11 Geometry (Curves and Surfaces)
Curves
- 应用
- 摄影机运动路径
- 动画路径
- 字体设计(矢量)
Bézier Curves
- 用一系列控制点,去定义一条曲线;属于显式的几何表示方法
计算贝塞尔曲线:de Casteljau Algorithm德卡斯特里奥算法
计算思路:递归
计算步骤
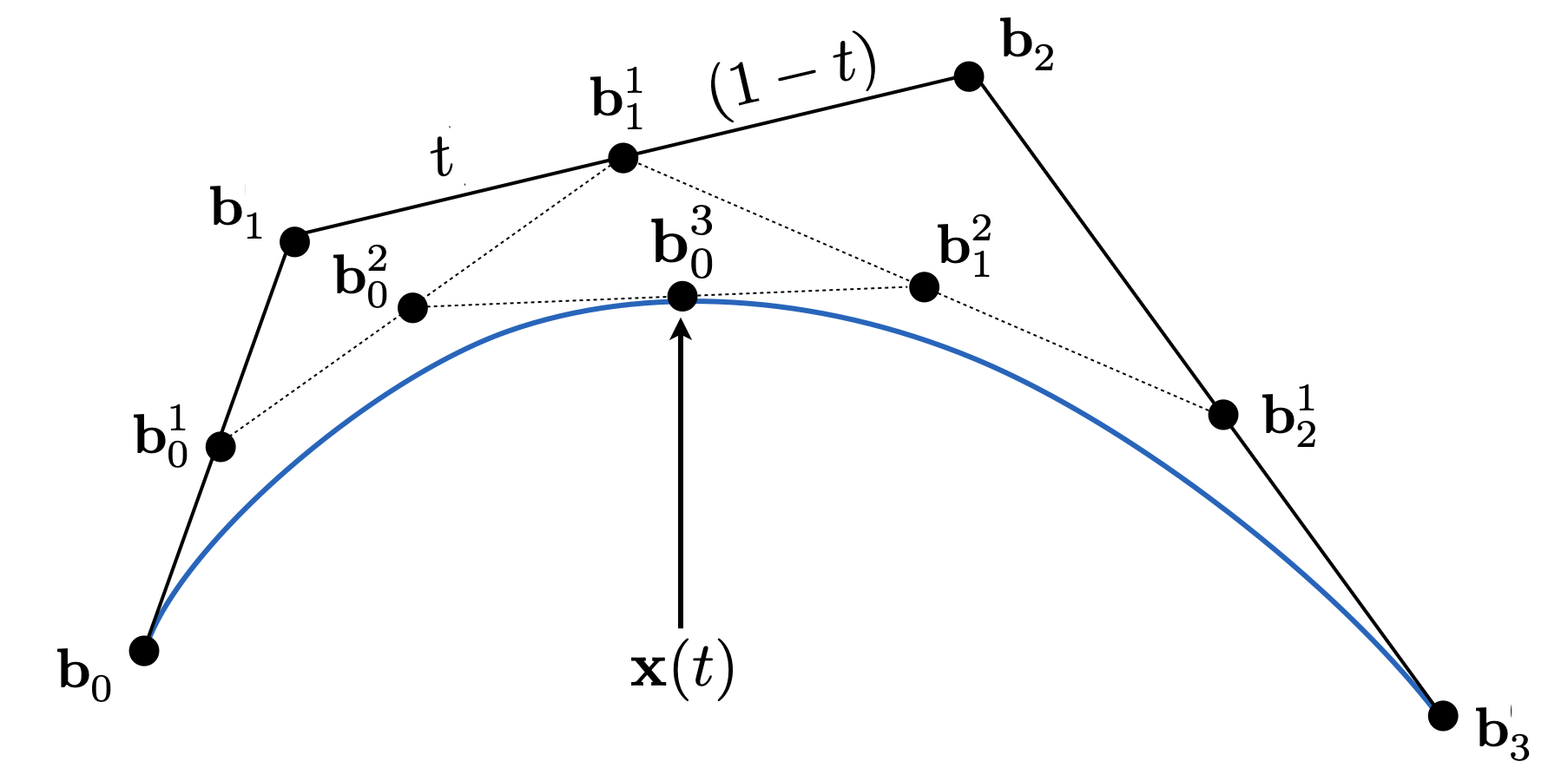
三个点:
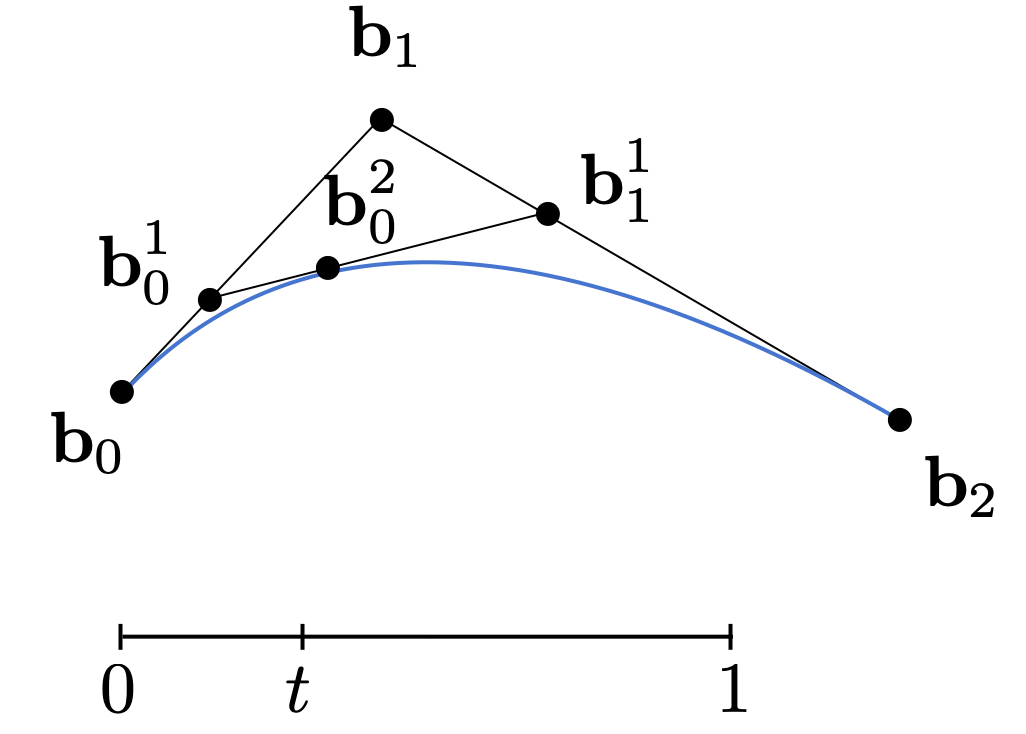
认为两个控制点间范围$(0,1)$
分别找到对应$t$的点的位置$b_0^1$和$b_1^1$,连接
再找到$b_0^1$$b_1^1$线段上$t$对应的点$b_0^2$
按上述方法,对$t$枚举,即可画出曲线
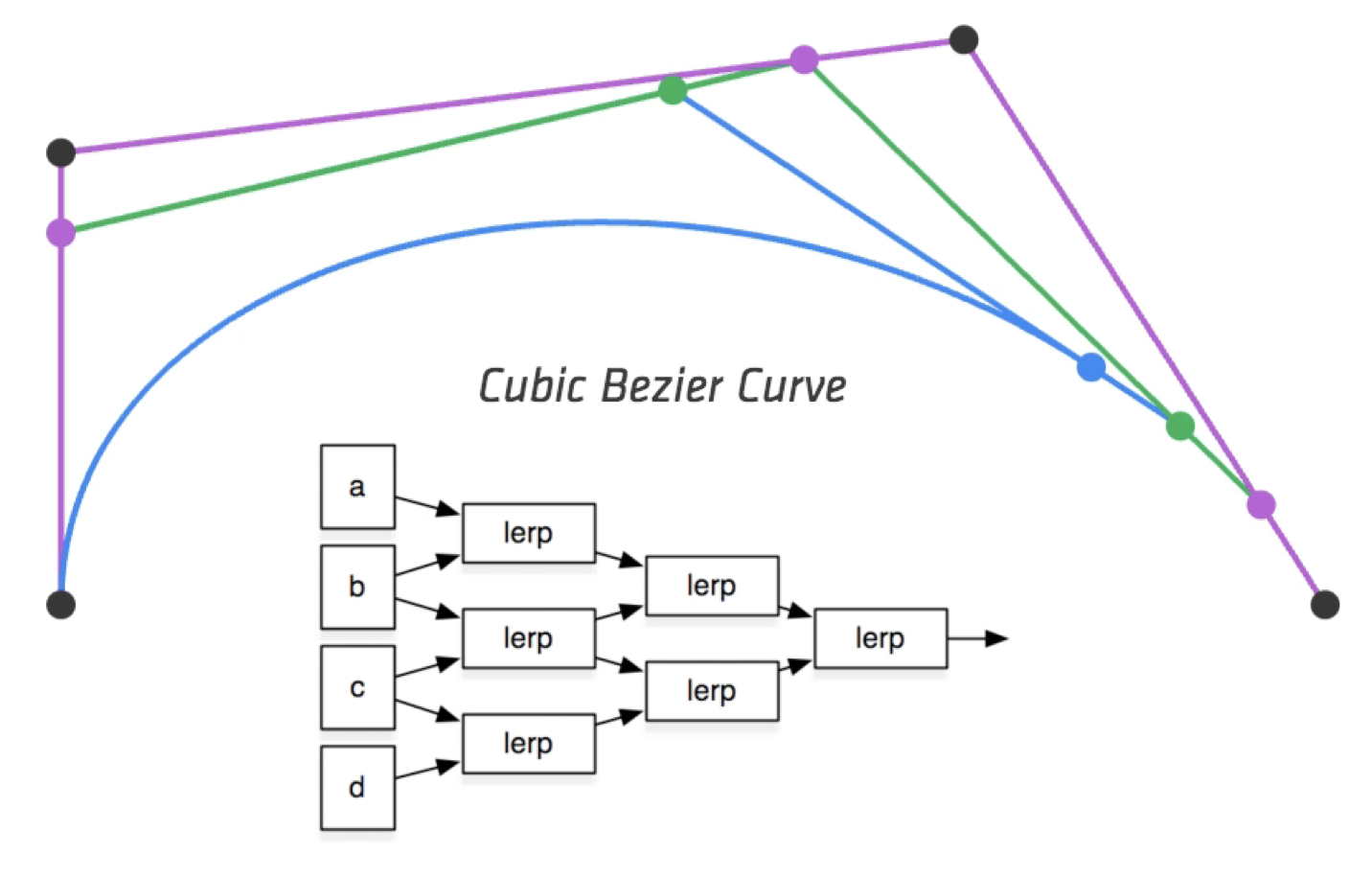
四个点:
代数公式
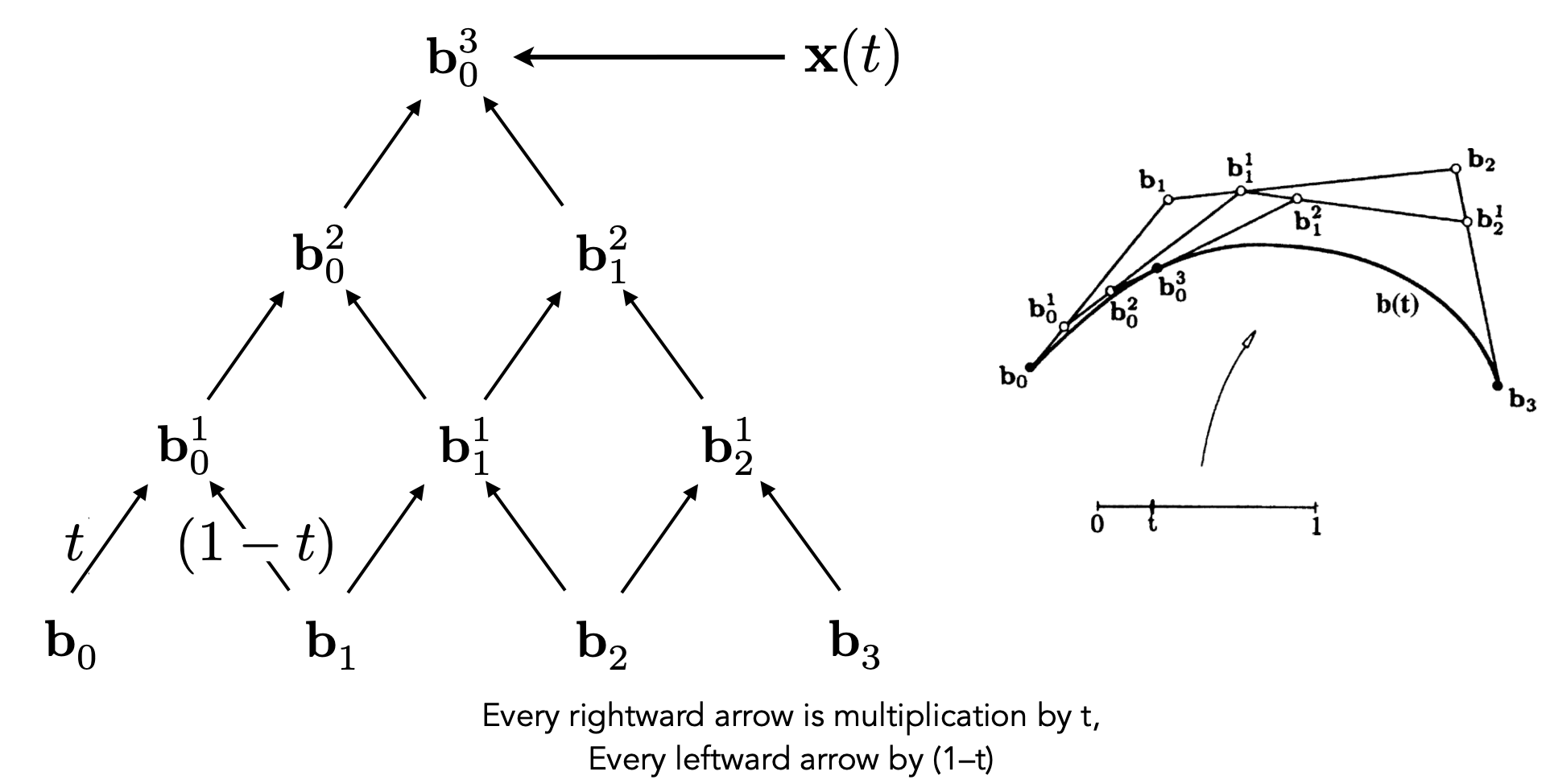
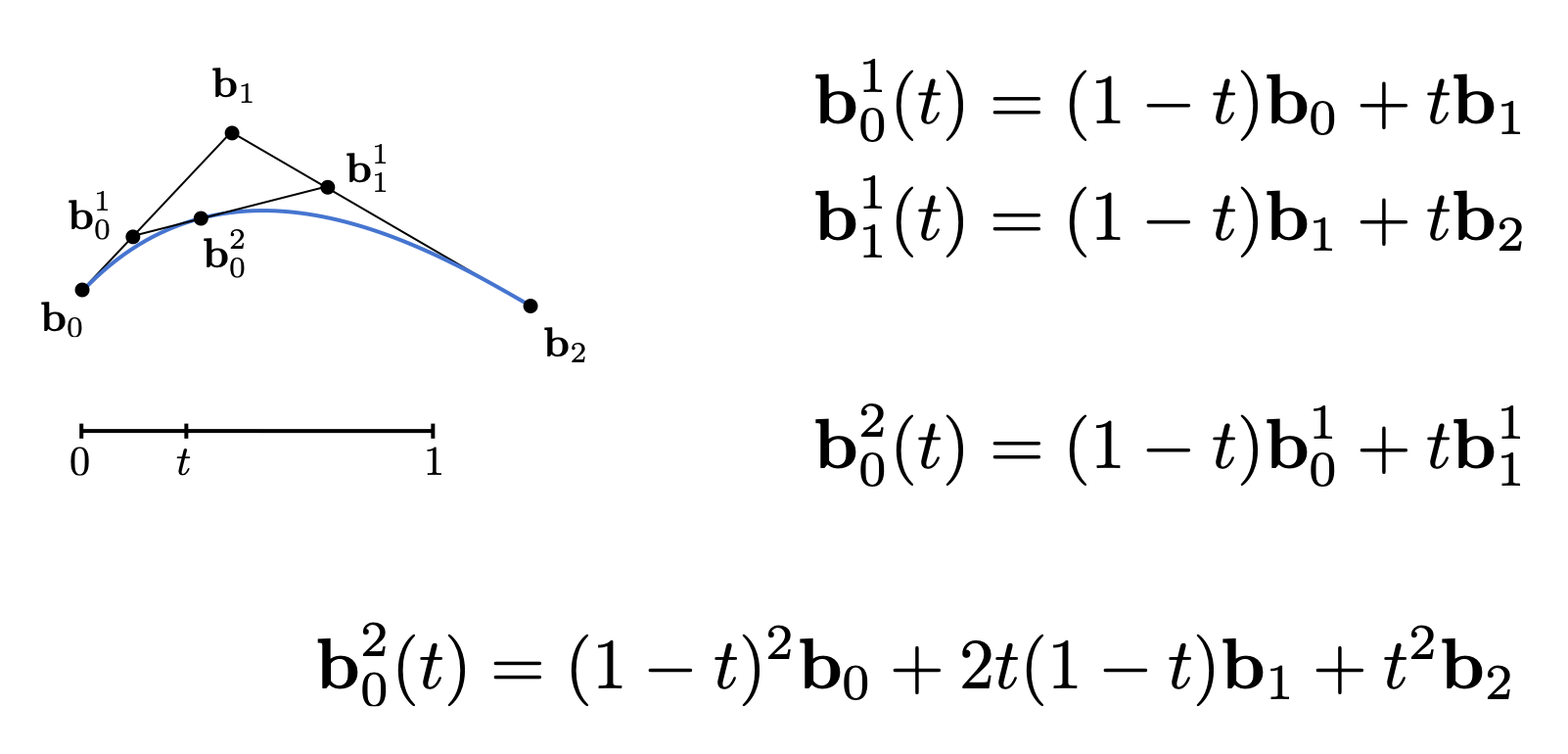
- $n+1$个控制点$(0,1,2,…,n)$可以得到$n$阶的贝塞尔曲线
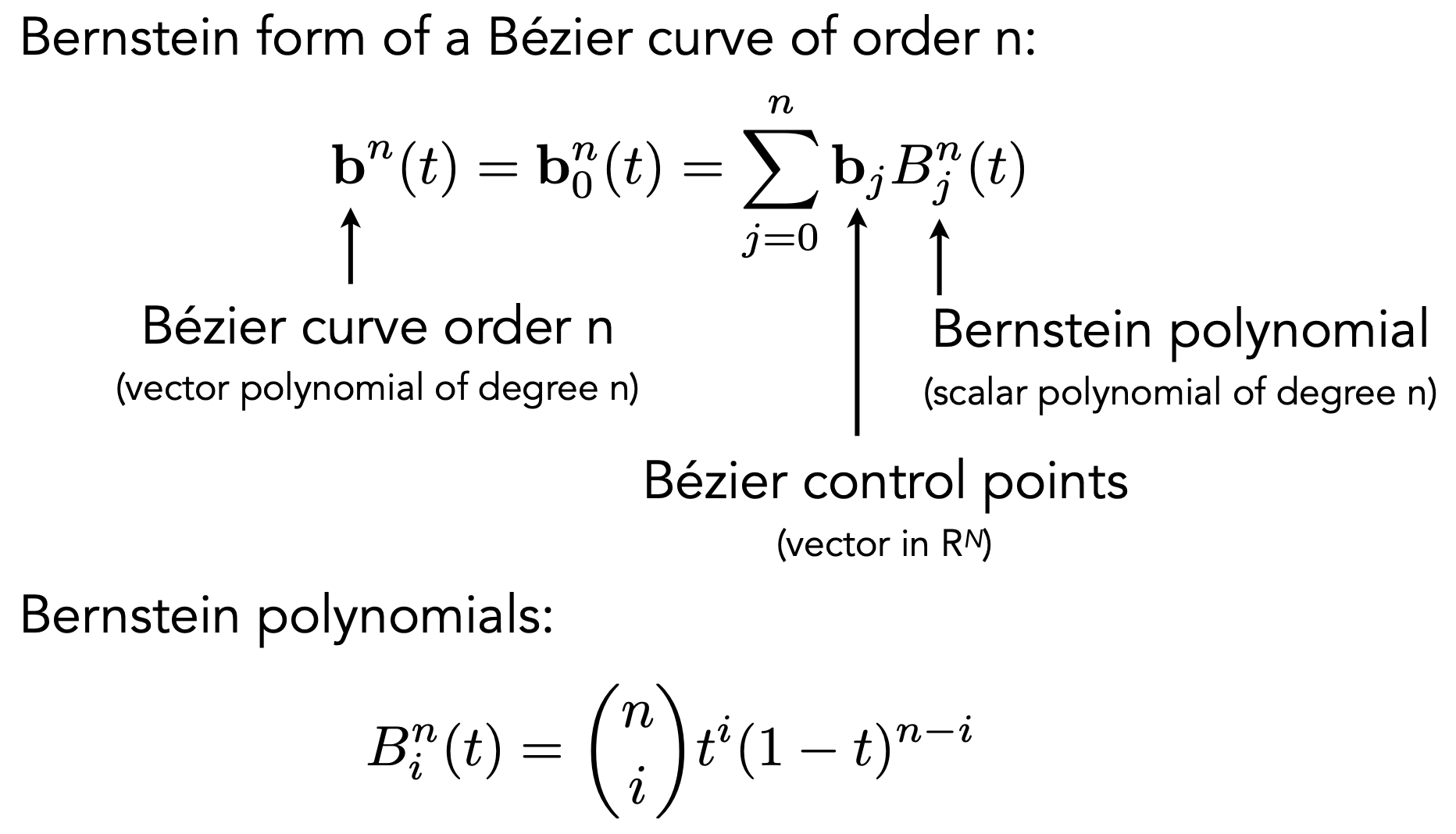

- $B_j^n(t) = C_n^i t^i (1-t)^{n-i}$:伯恩斯坦多项式
- 其实是$[t+(1-t)]^n = 1^n$的二项式展开的每一项,因此下图y方向,和为1
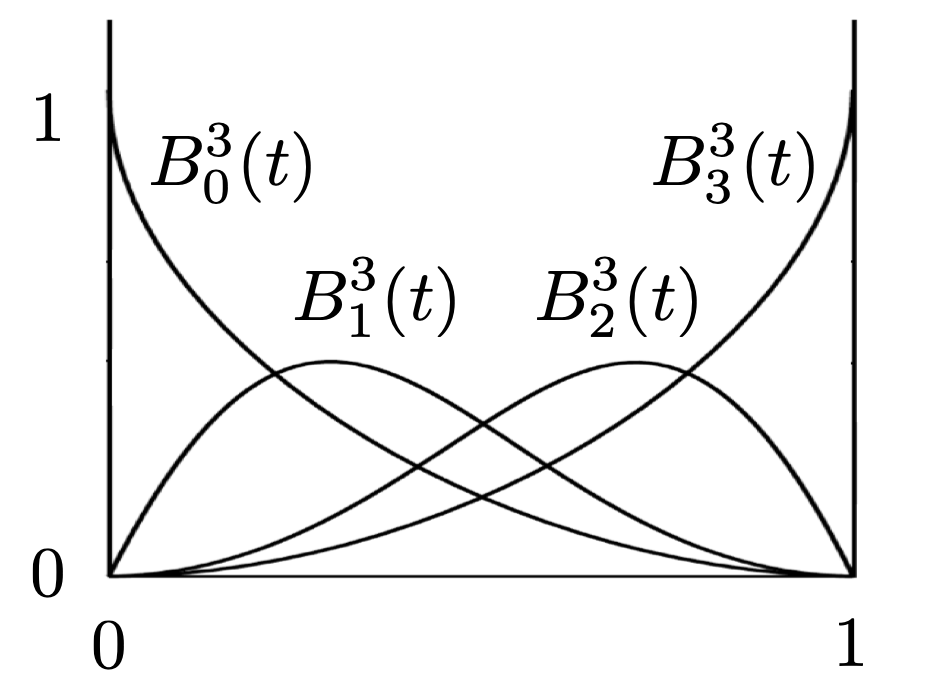
性质

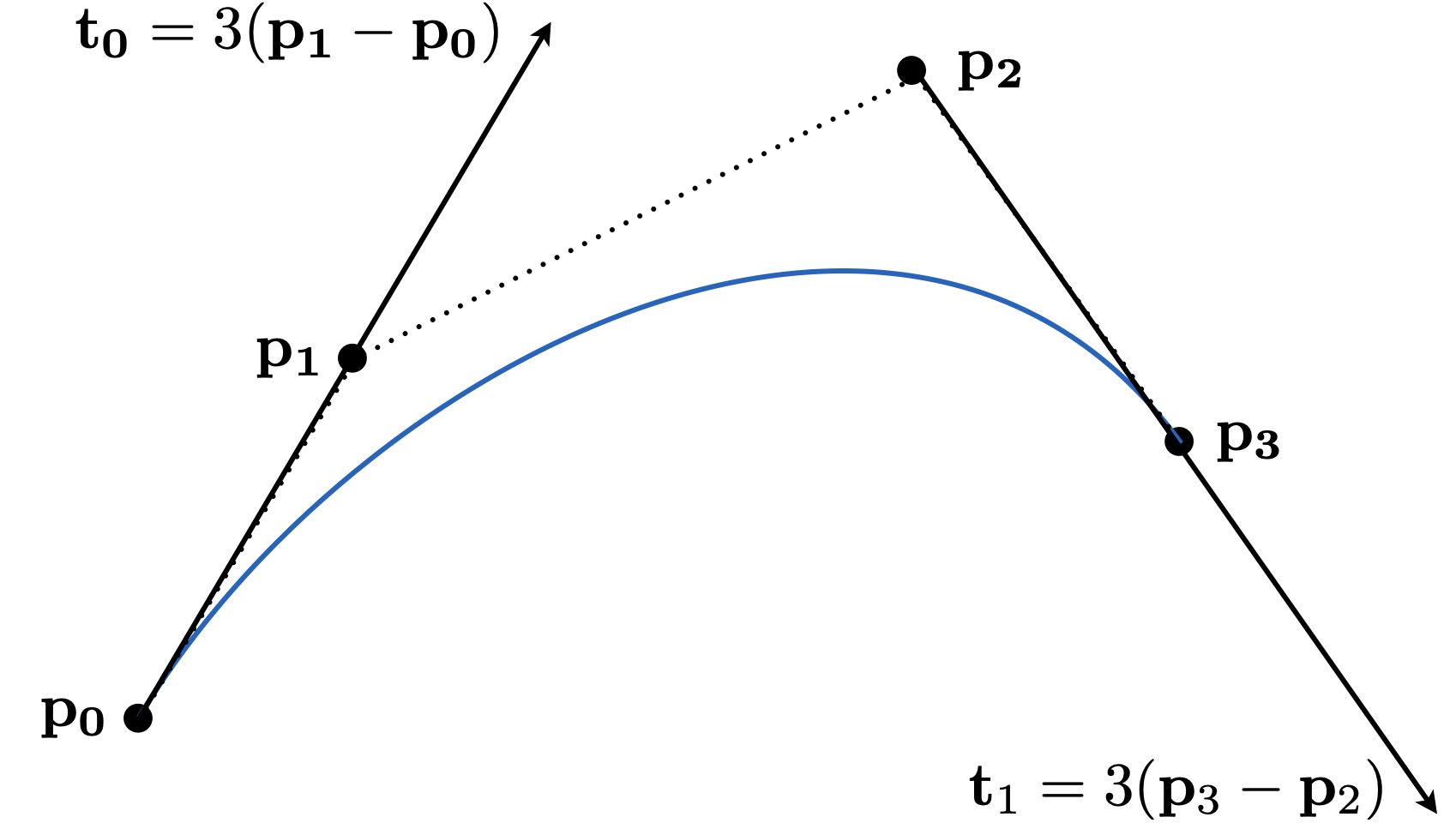
必过起点和终点。则$t=0$时$b(0) = b_0$,$t=1$时$b(1) = b_3$
对三次控制点:切线$b’(0)=3(b_1-b_0)$,$b’(1) = 3(b_3-b_2)$。针对系数3,通过求导可知
对于仿射变换:针对控制点的变换,和针对曲线本身的变换,得到的结果相同
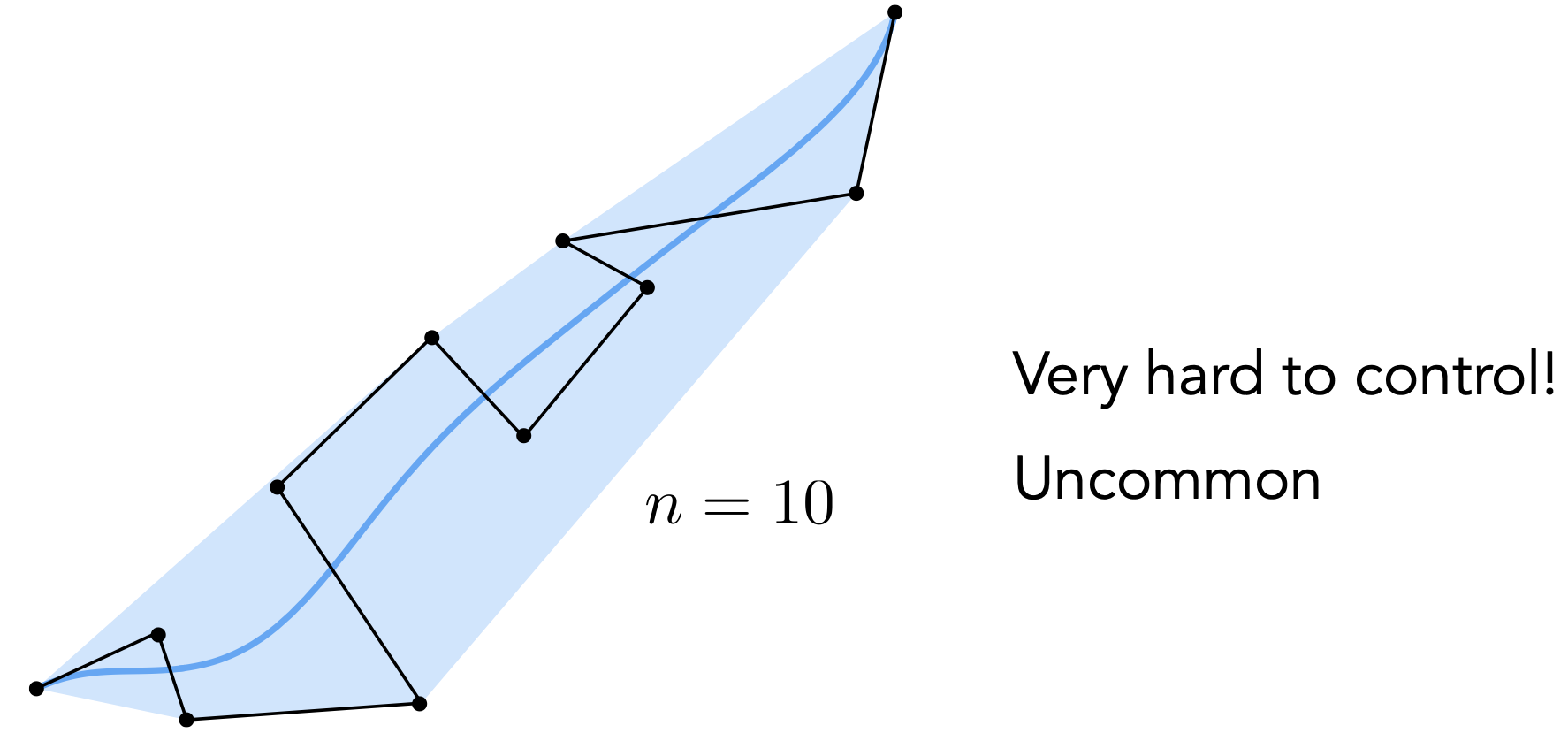
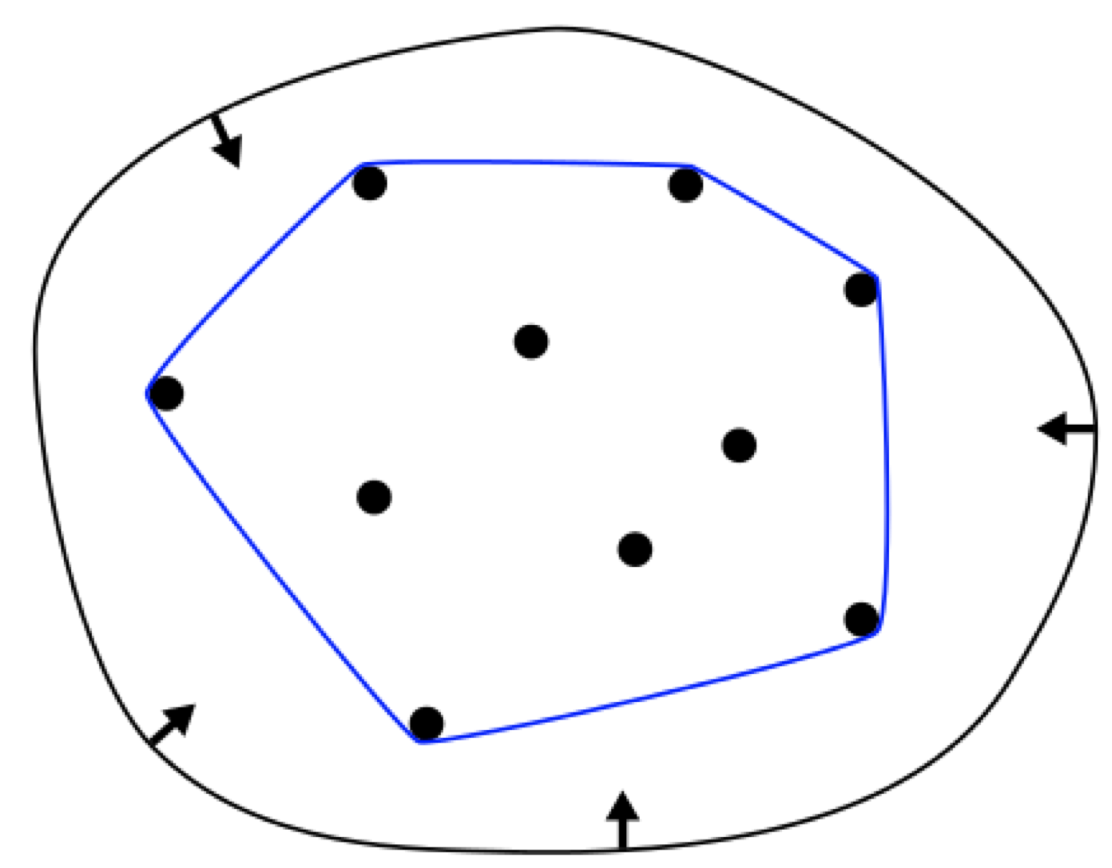
凸包性质:贝塞尔曲线在控制点所形成的凸包内
Piecewise Bézier Curves 逐段贝塞尔曲线
- 思路
- 问题:控制点难以直观控制曲线:
- 解决:试图用四个控制点控制一段贝塞尔曲线:
- 问题:控制点难以直观控制曲线:
- 连续情况
- $C^0$连续:前一段截止点 = 下一段起始点
- $C^1$连续
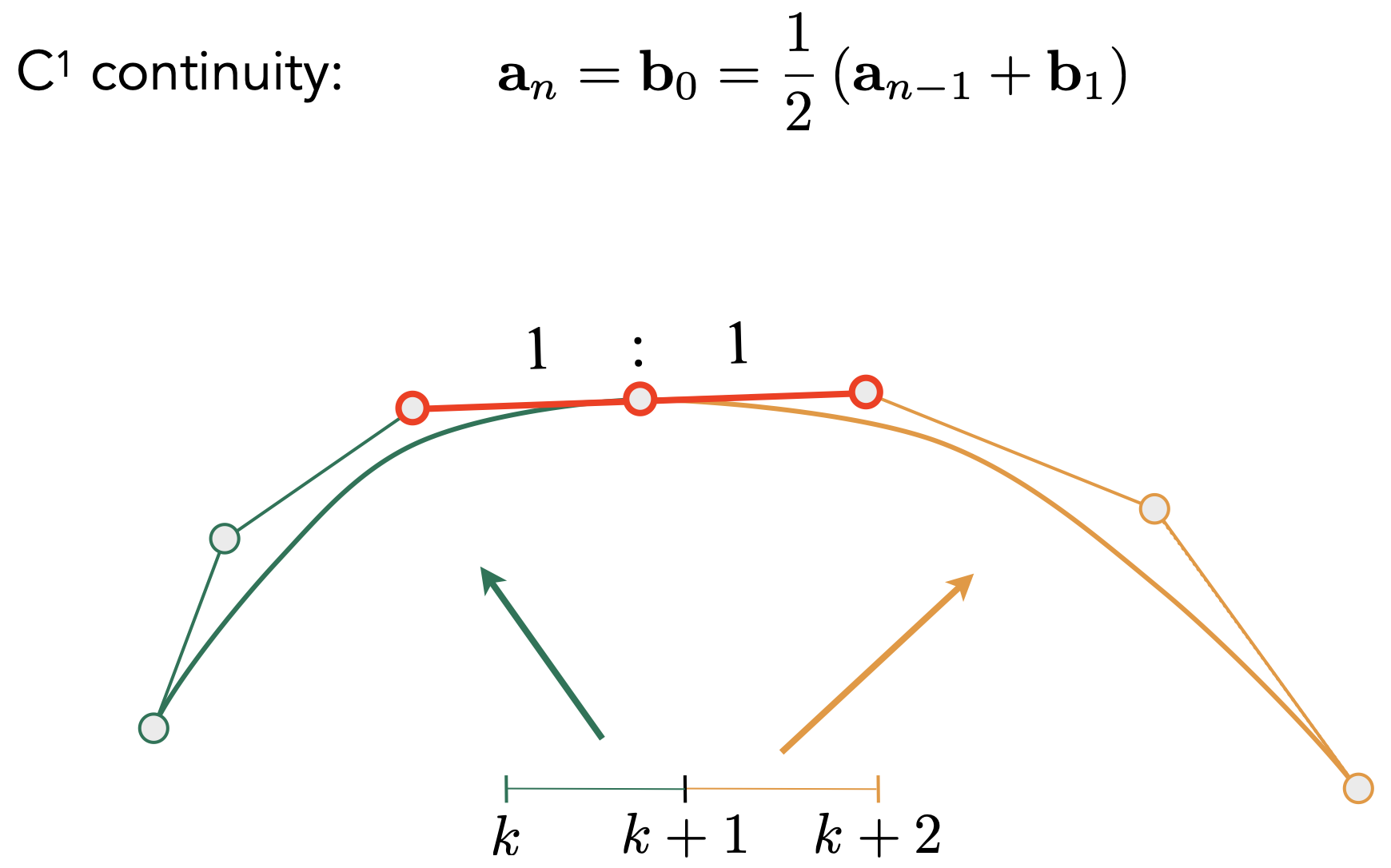
- $C^n$连续:n阶导数连续
其他曲线
- Spline 样条曲线

- B-Spline
- Base spline
- 局部性
- Nurbs
Surfaces
- Bicubic Bézier Surface
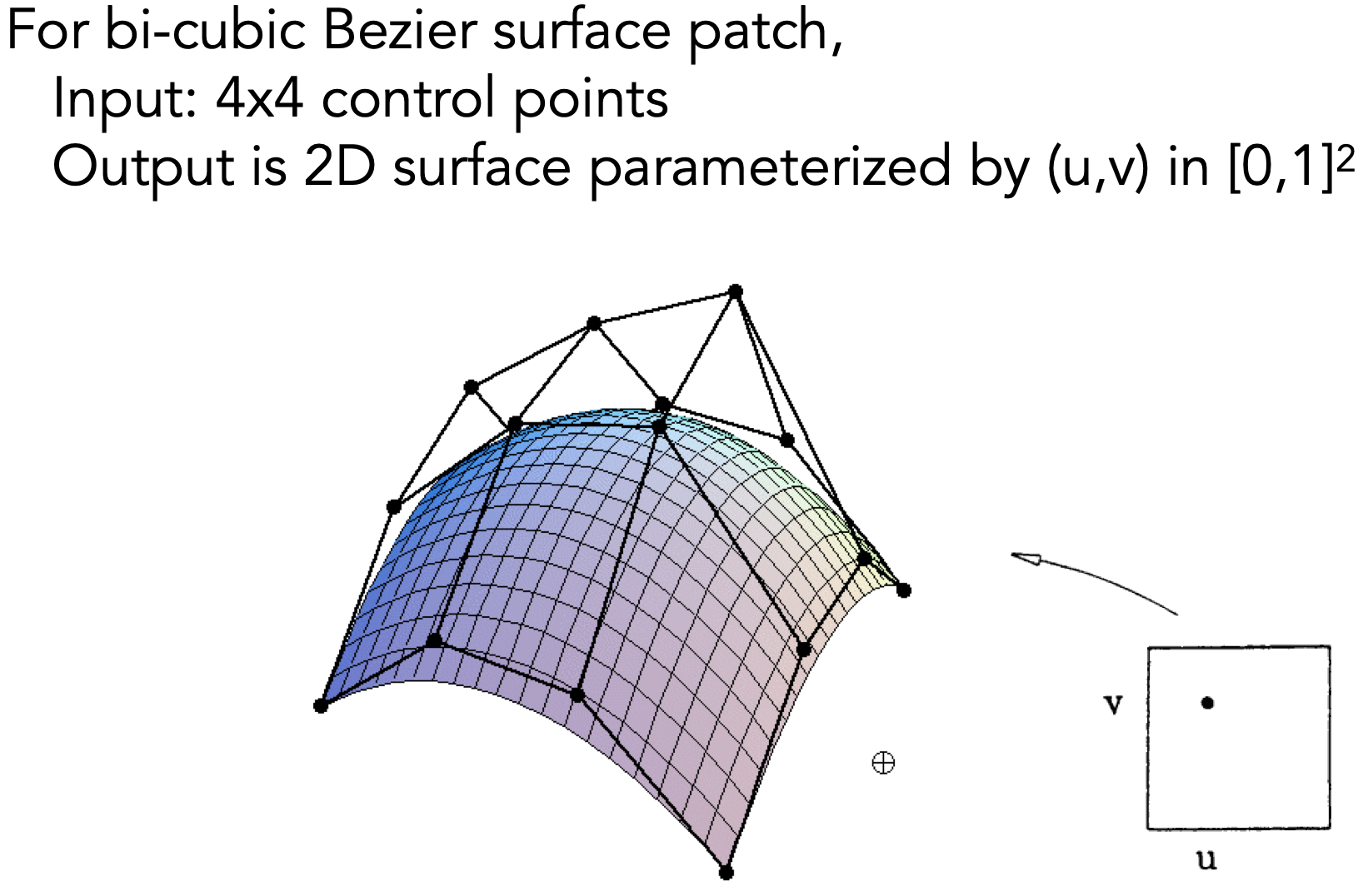
- 思路:
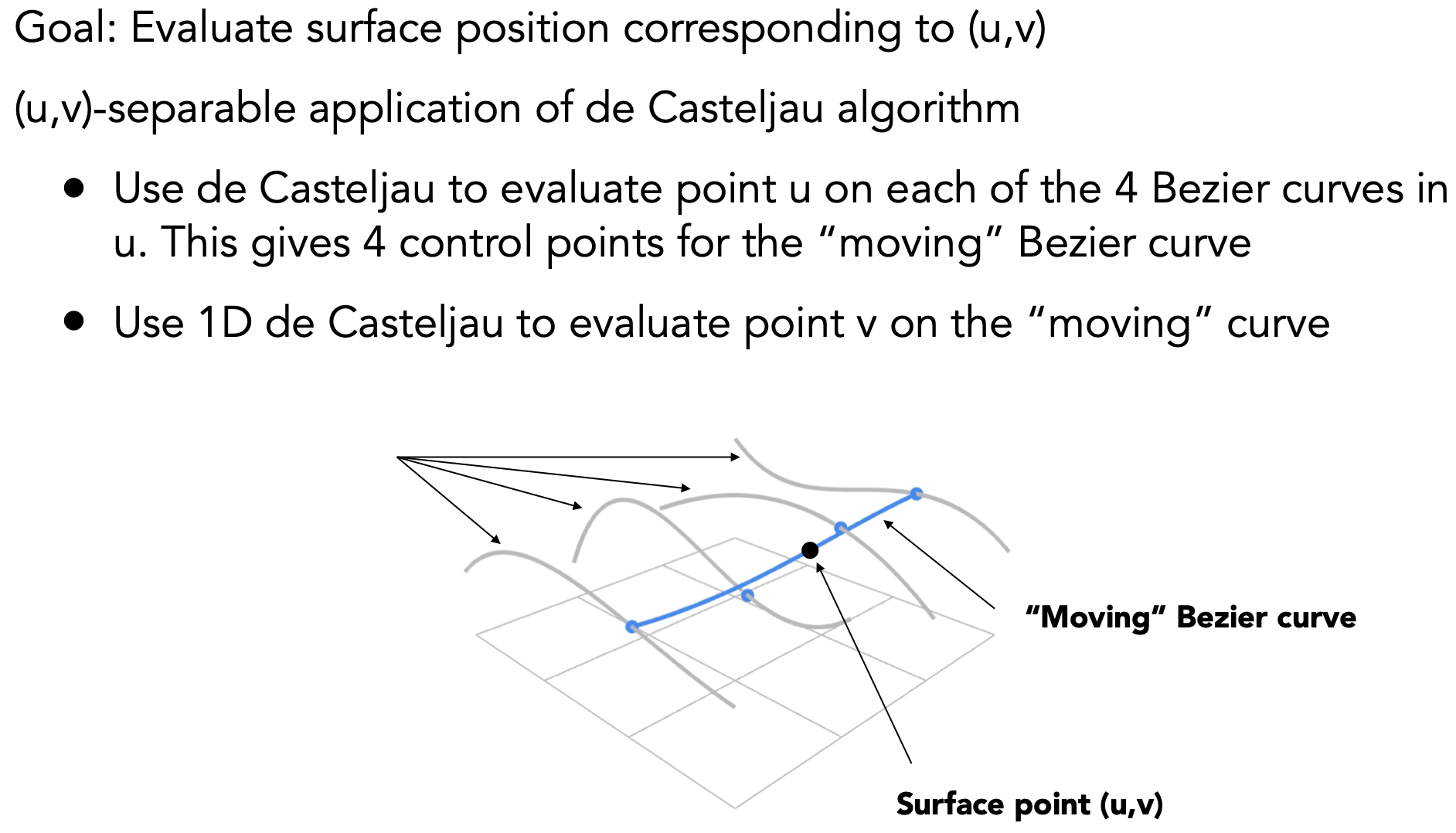
- u方向控制点得出四条贝塞尔曲线,每一时刻t在四条曲线上的四个控制点为v方向对应贝塞尔曲线的控制点;v方向贝塞尔曲线扫过的面为对应曲面
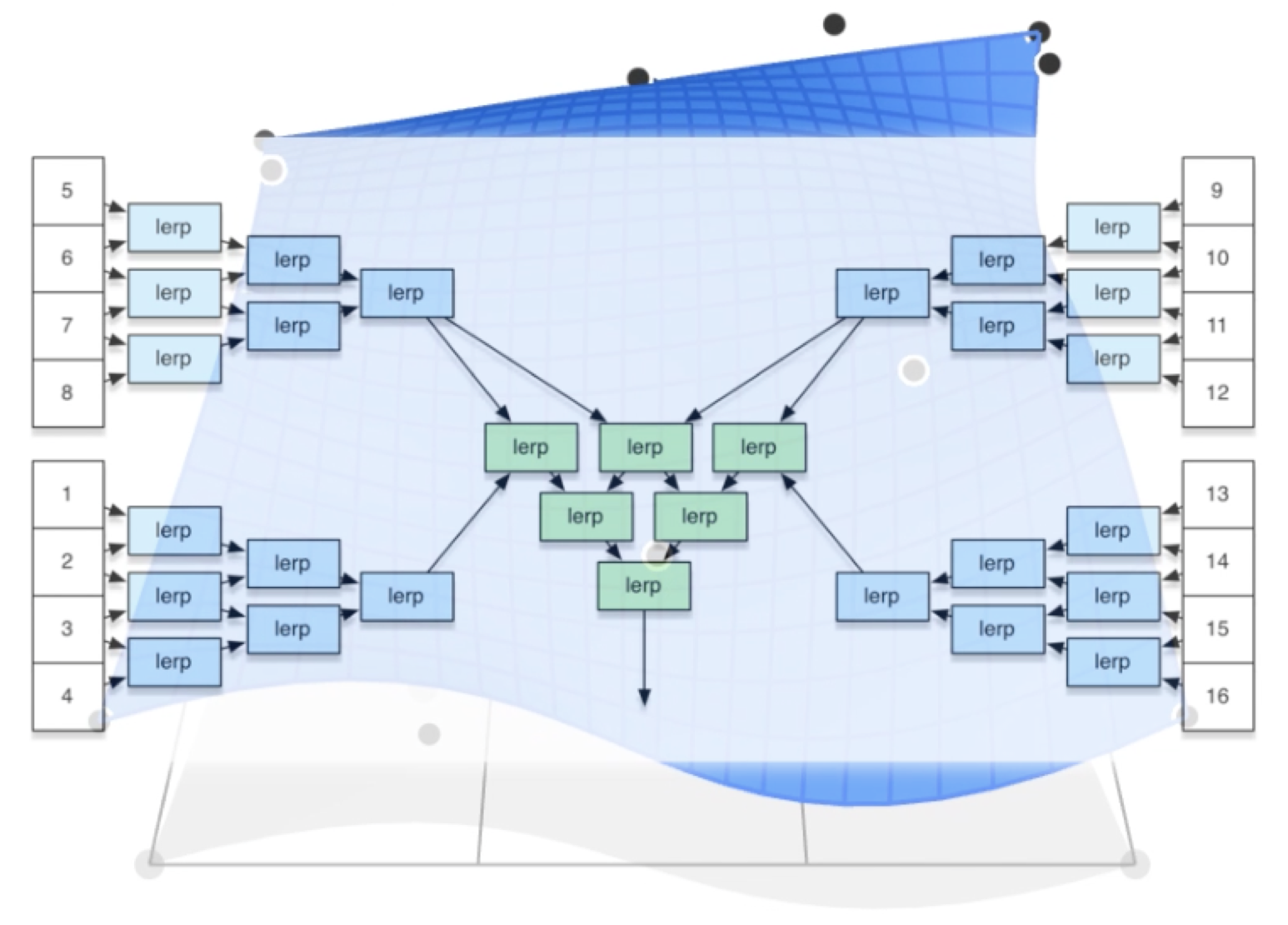
- Mesh Operations: Geometry Processing
P12 Geometry
Mesh Subdivision (upsampling)

Loop Subdivision
只适用于三角形网格
步骤
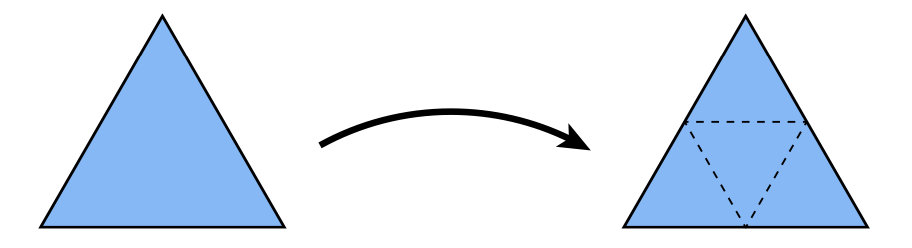
- 增加三角面,$\times 4$
- 使模型表面变光滑(调整顶点位置)
- 新/旧顶点已不同形式改变
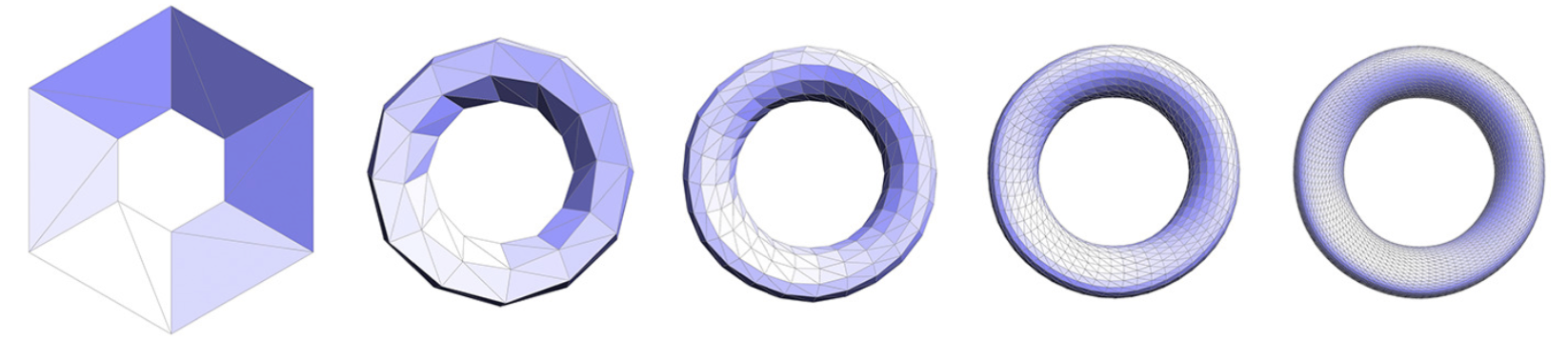
- 增加三角面,$\times 4$
更新顶点位置的规则
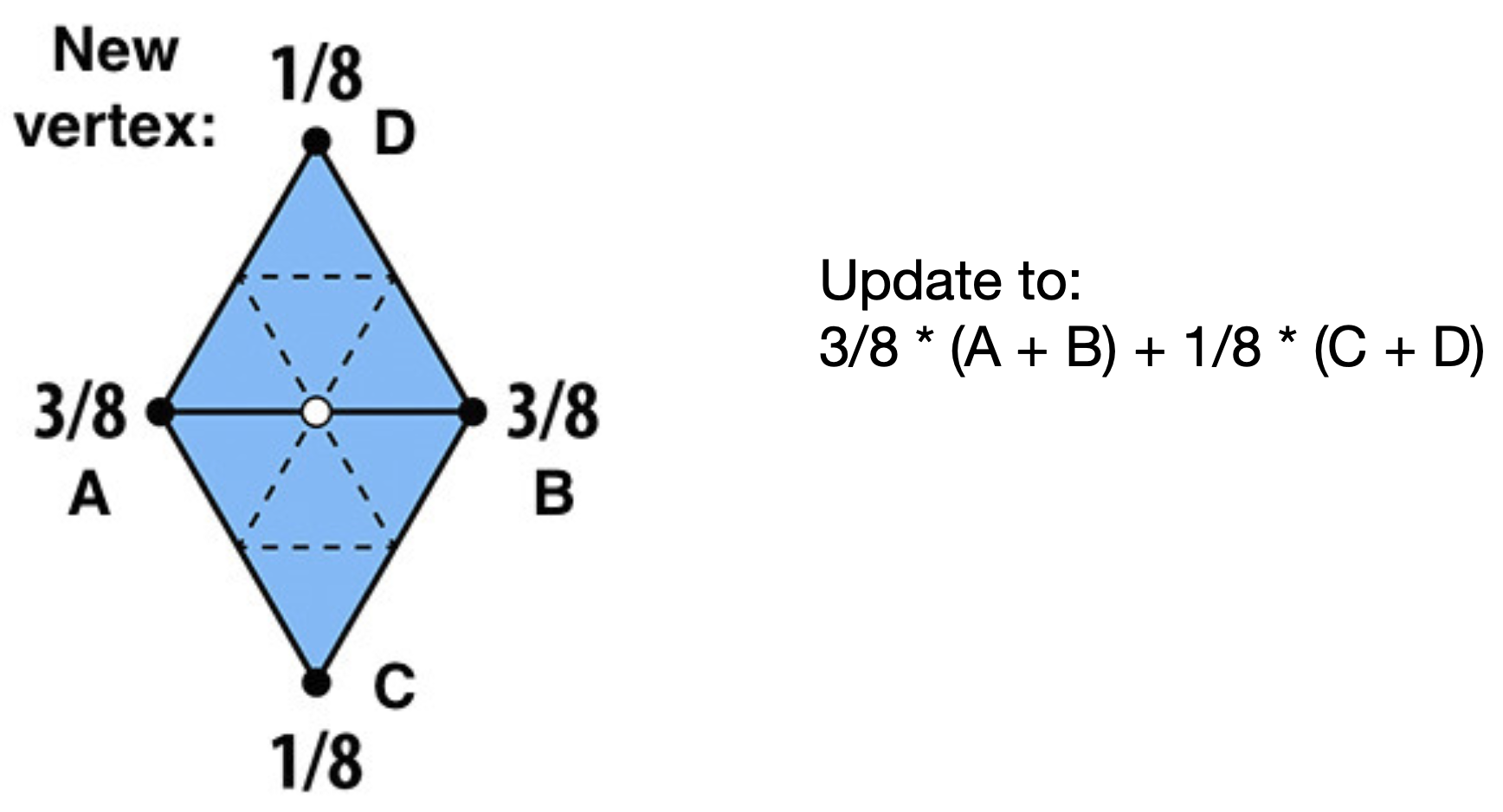
- 对于新的(不为边界的)点
- 对于旧的点 (e.g. degree 6 vertices here)
- n:顶点的度,即为顶点所连接的边的个数
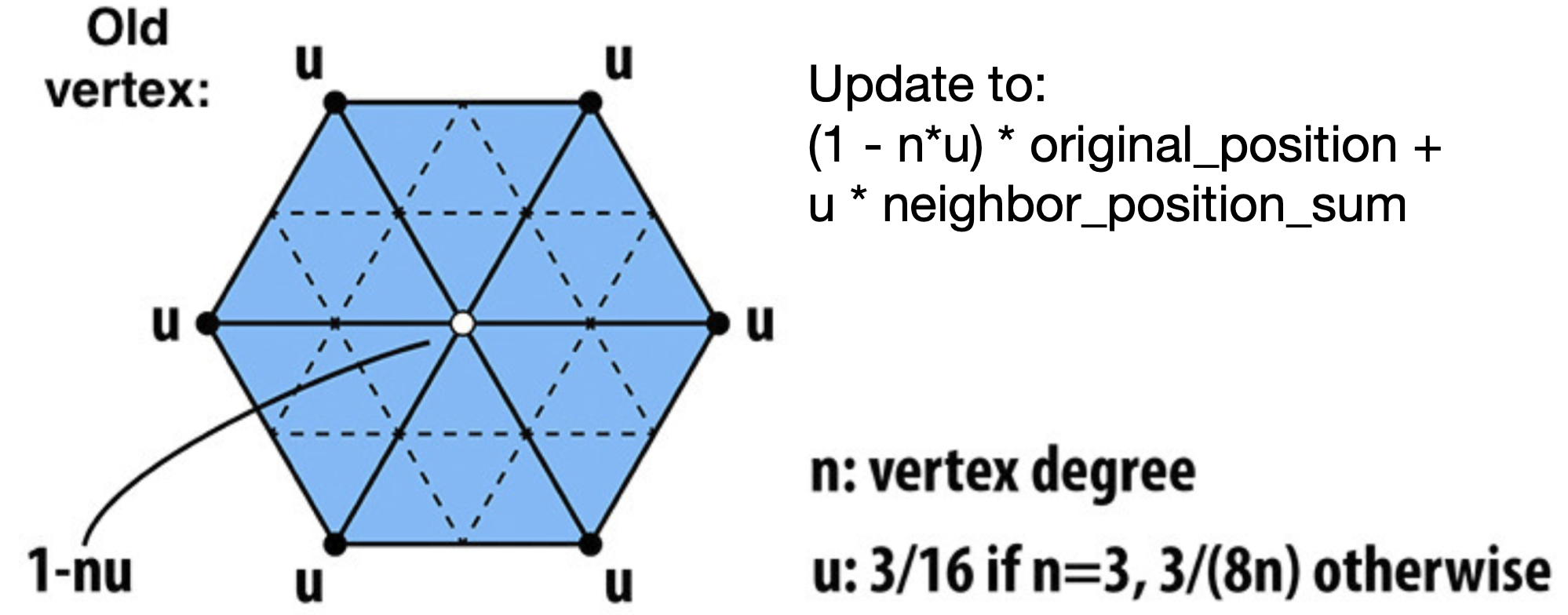
- 对于新的(不为边界的)点
Catmull-Clark Subdivision (General Mesh)
- 适用于三角面和四边面
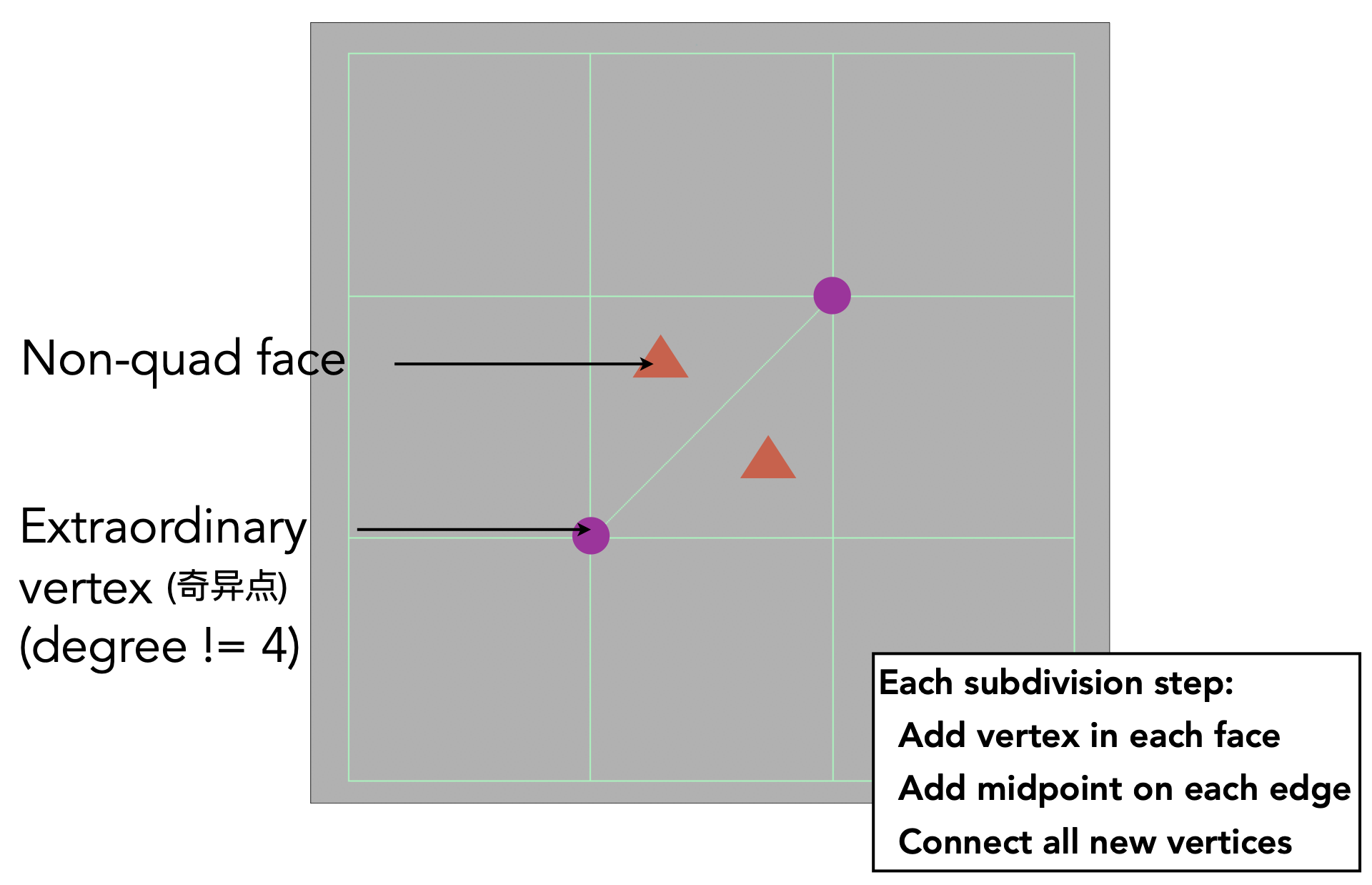
- 奇异点:度不为4的点
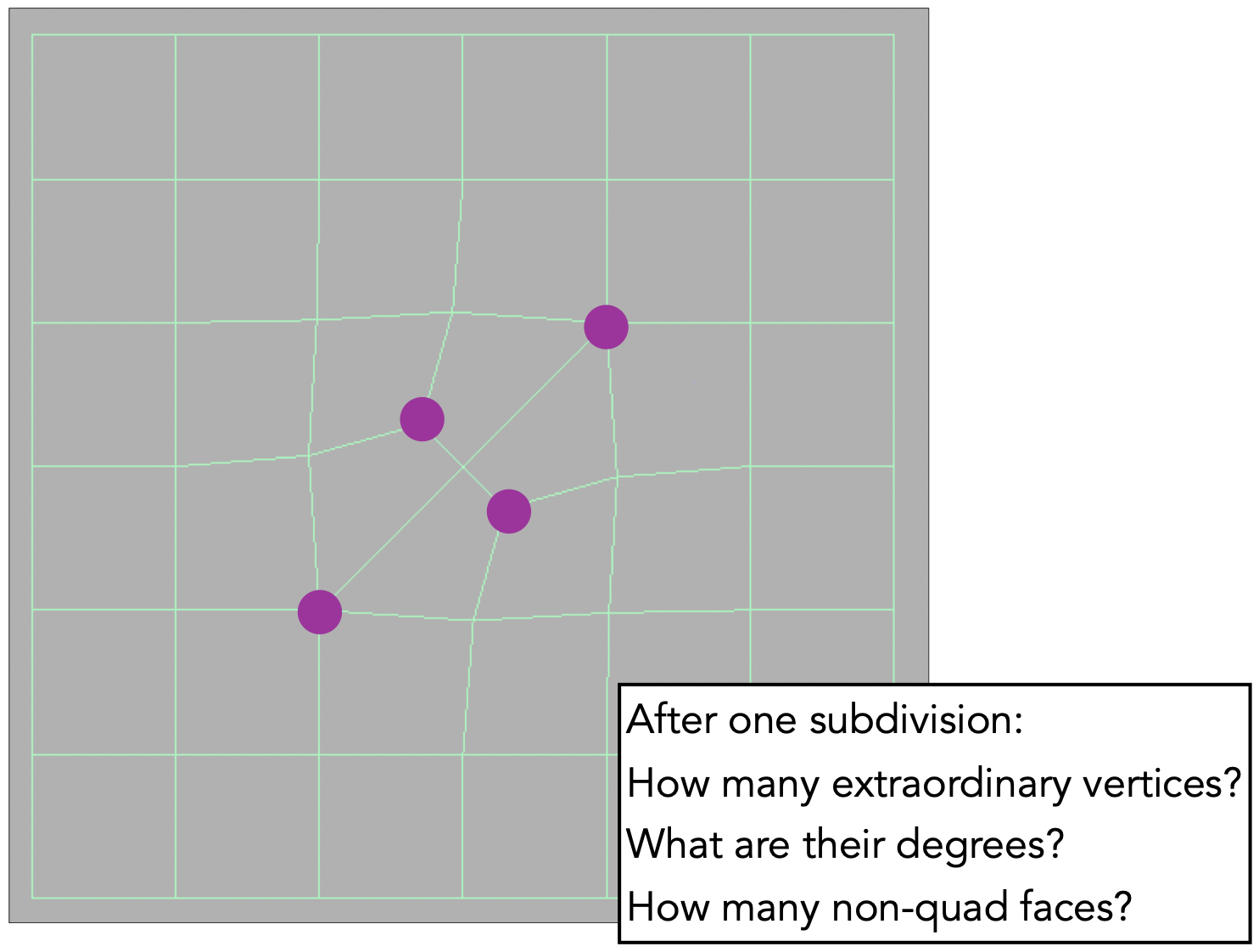
- 非四边形面消失并引入奇异点
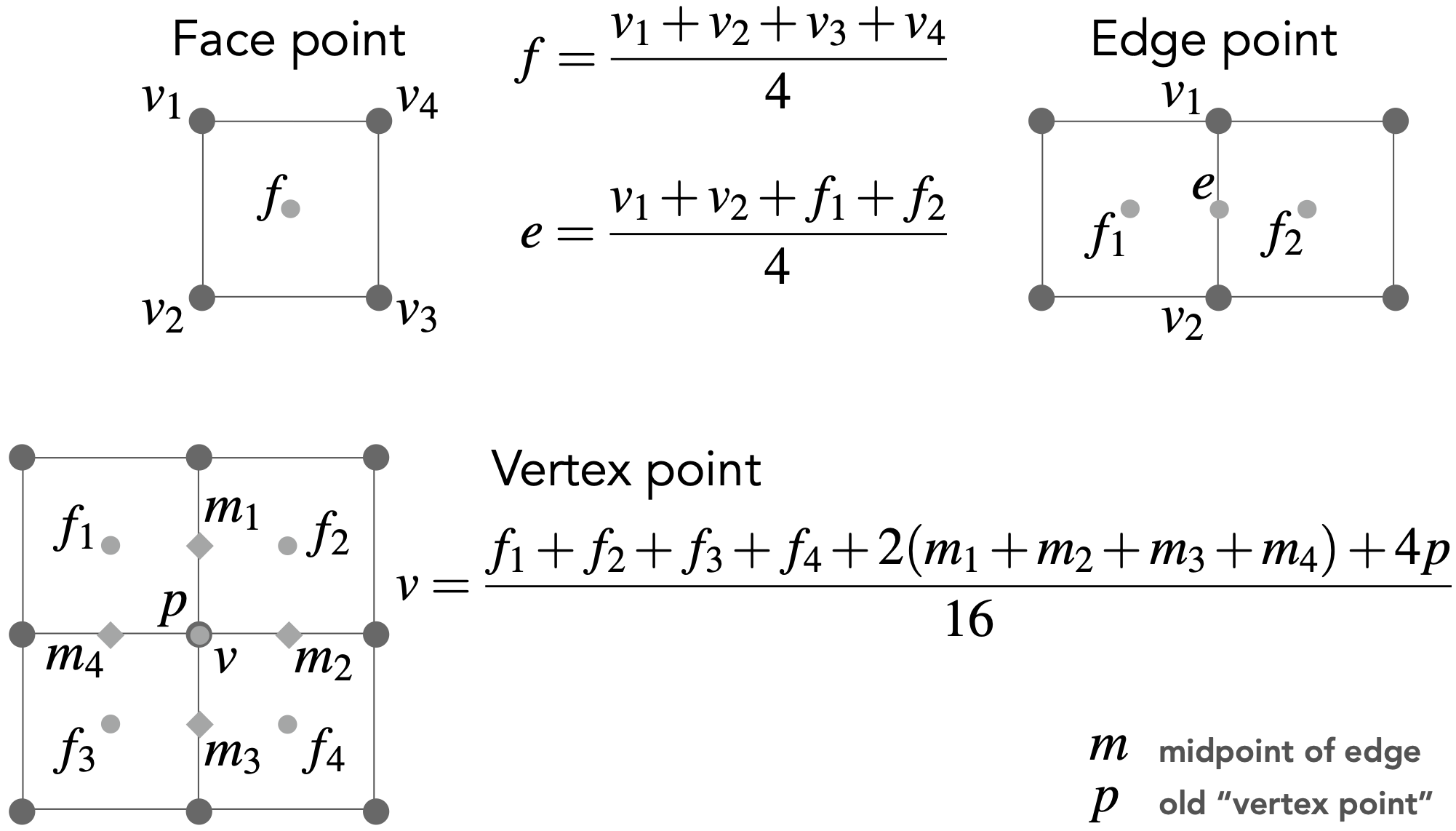
- 新顶点位置的规则
结果对比

Mesh Simplification (downsampling)
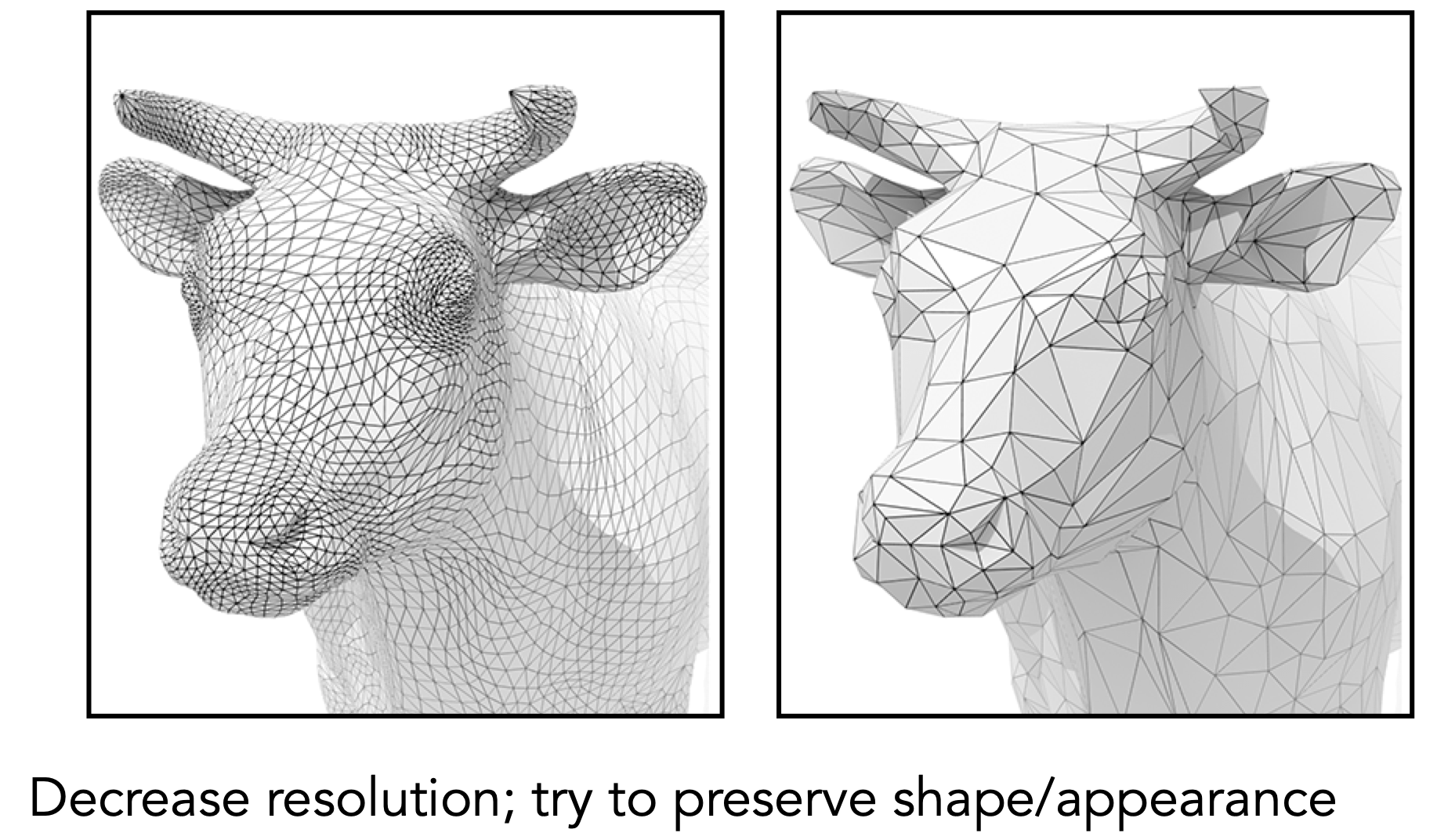
- 目标:减少面数的同时,保持物体原有的大致形状
- 联系Mipmap(也可以联系LOD),依据情况做simplification
简化方法
Collapsing An Edge 边坍缩
http://graphics.stanford.edu/courses/cs468-10-fall/LectureSlides/08_Simplification.pdf
(距离其中一种简化方法)
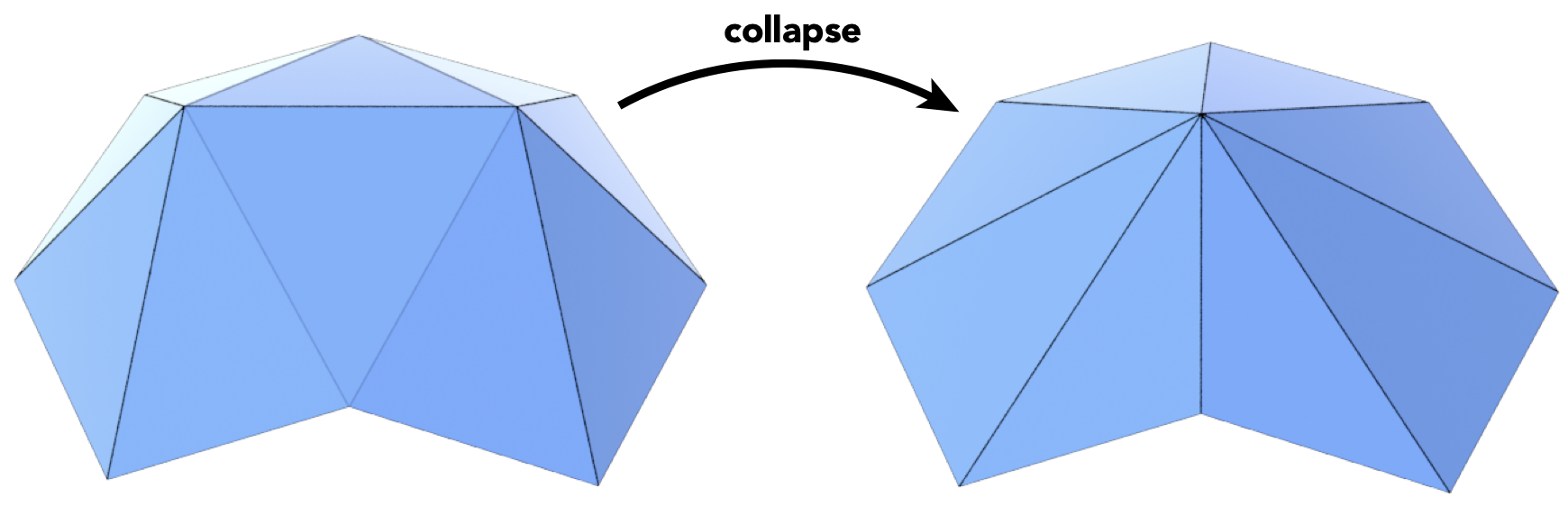
- 如何判断坍缩的边:Quadric Error Metrics (QEM二次误差度量)
- 对顶点进行局部平均不是一个好主意
- 二次误差度量:新的顶点需满足到其所联系的面的距离平方和最小
- 如何坍缩对面影响最小——二次度量误差最小
- 基本思想:算每一条边的二次度量误差,从最小的开始坍缩
- 问题:坍缩一条边,相连的边发生变化,二次度量误差随之变化
- 解决:堆,优先排序,取QEM最小的坍缩,并动态更新所被影响的边的QEM
Mesh Regularization (same #triangles)