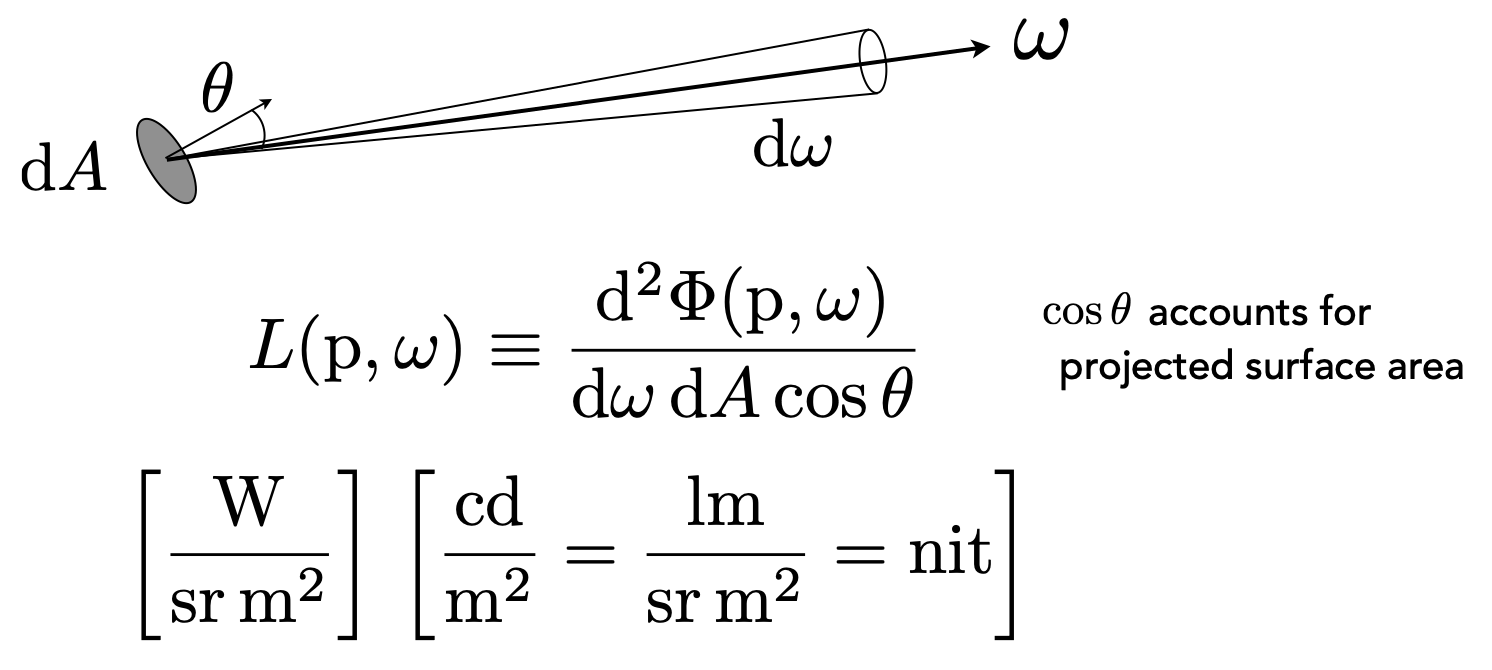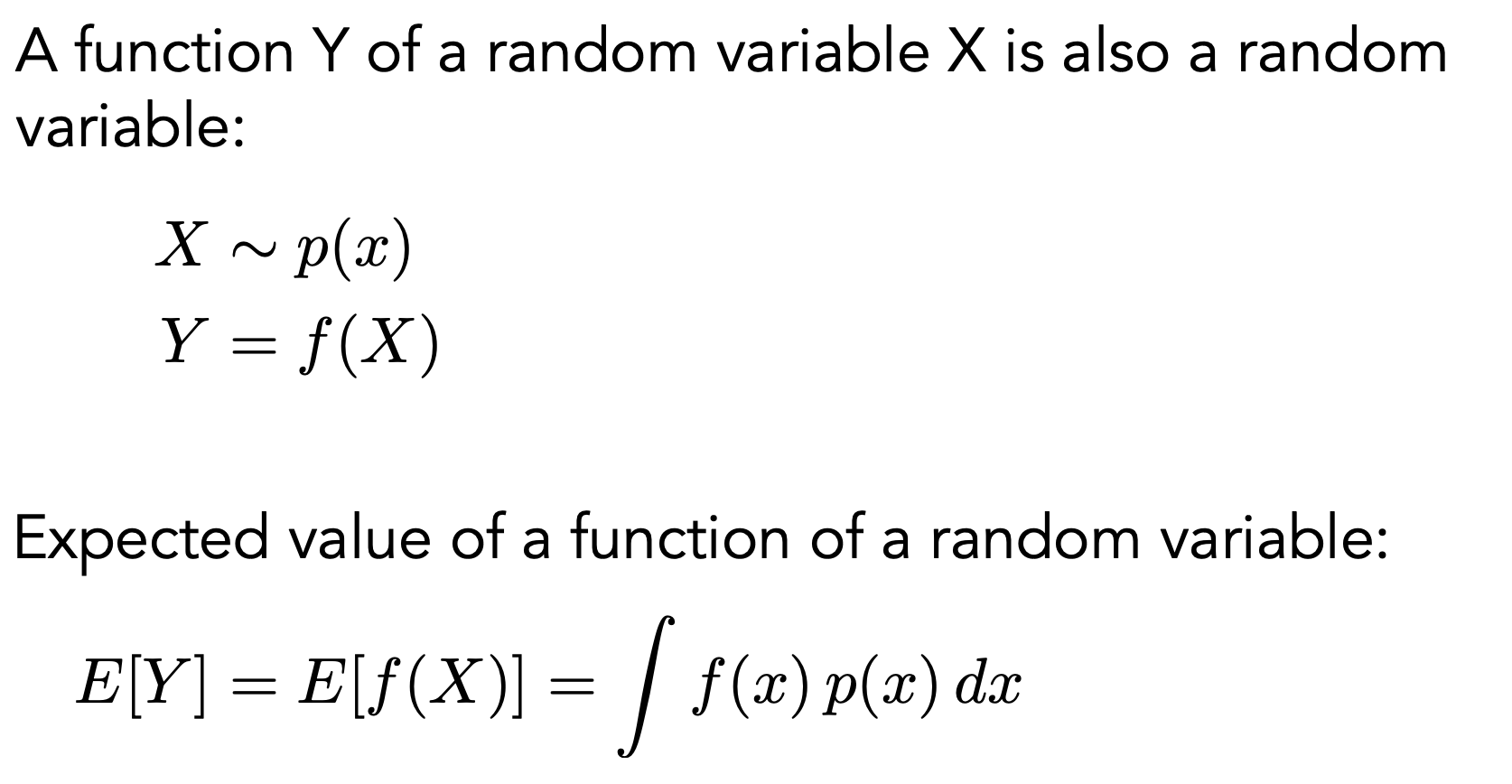Games101-P13-16 Ray Tracing

Posted on 2023-04-23 Edited on 2023-07-30 In Games101 Word count in article: 9.2k

P13 Preview
- Recursive (Whitted-Style) Ray Tracing
  - Ray-Surface Intersection 光线和面求交：球体、隐式表面、三角面，及缺点
- Accelerating Ray-Surface Intersection 加速
  - Ray Intersection with Axis-Aligned Box
P14&15 Preview
- Using AABBs to accelerate ray tracing
  - Uniform grids
  - Spatial partitions 空间划分
    - KD-Trees
    - BVHs
- Basic radiometry
  - Radiant Energy $Q$ and Flux(Power) $\Phi$
  - Intensity $I$：power per projected unit area
  - Irradiance $E$：power per unit area
  - Radiance $L$：power per unit solid angle & per projected unit area
- BRDF：是针对一个方向，出射Radiance($dL_r(\omega_r)$)/入射Irradiance($dE(\omega _i)$)的比例
  - 反射方程
  - 渲染方程
- 概率论回顾
P16 Overview
- Monte Carlo Integration
- Path Tracing
  - PT 优化

P13 Ray Tracing 1

Why ray tracing?
- 光栅化渲染不能完美诠释global effects(下图都算global effect)
- 光栅化速度快，可实现近似，但质量较低
- 光栅化是Real-time；光线追踪是Offline
Features of ray-tracing
- accurate
- slow

Basic Ray-Tracing Algorithm

Intro

Light光线
- 光线延直线传播（本课中）
- 光线相交时不会发生碰撞（本课中）
- 光线从光源发射出，经反射、折射后进入人眼

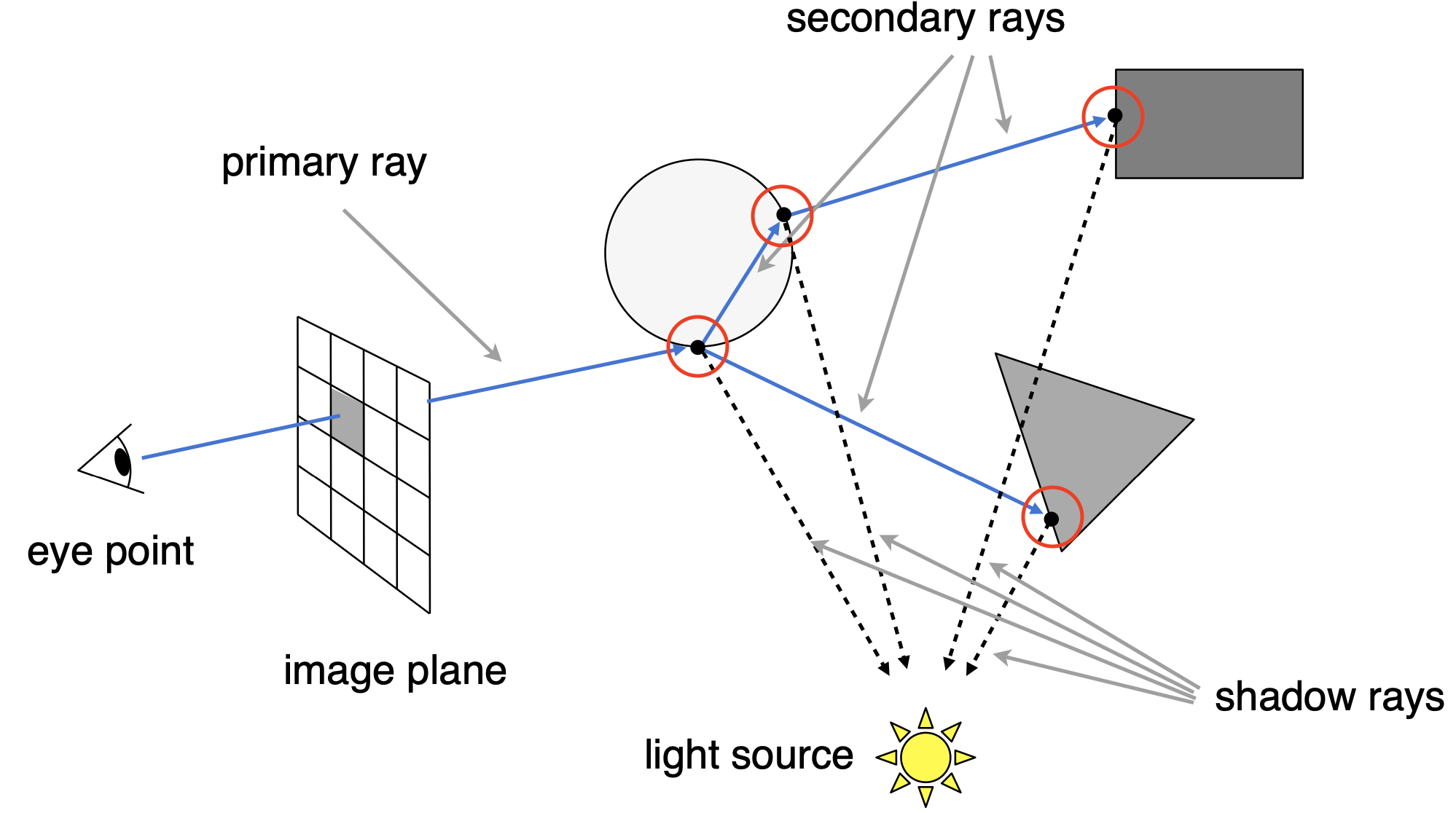
Ray Casting

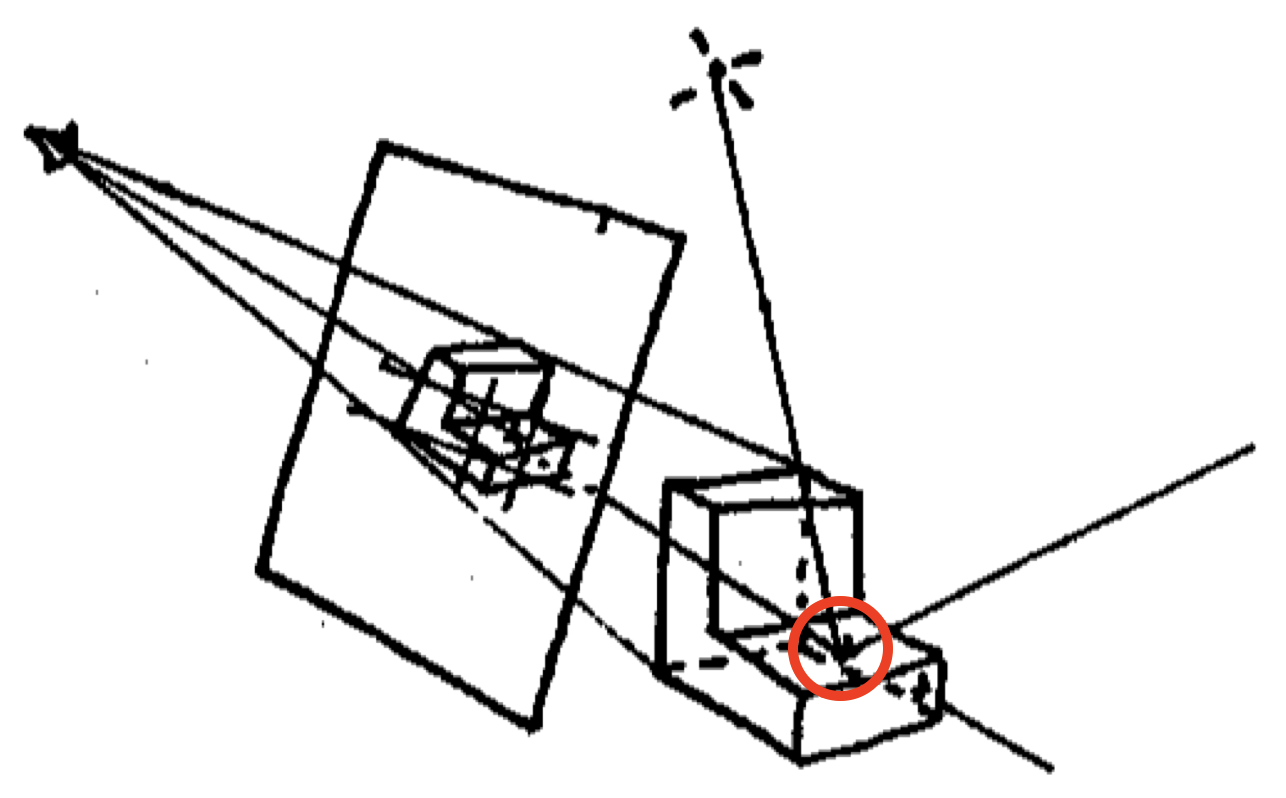
截屏2023-04-23 23.15.03

概述
- 摄像机与屏幕像素连线，并穿透屏幕并打在红圈处
- 连接红圈和光源，判断红圈处点是否在阴影中
- 若不在阴影中，则该光线有效，可进行进一步计算该点处光的能量

Generating Eye Rays

Pinhole Camera Model 针孔相机模型
- Step1: 每一个像素的光线射入，与场景相交，求出最近交点
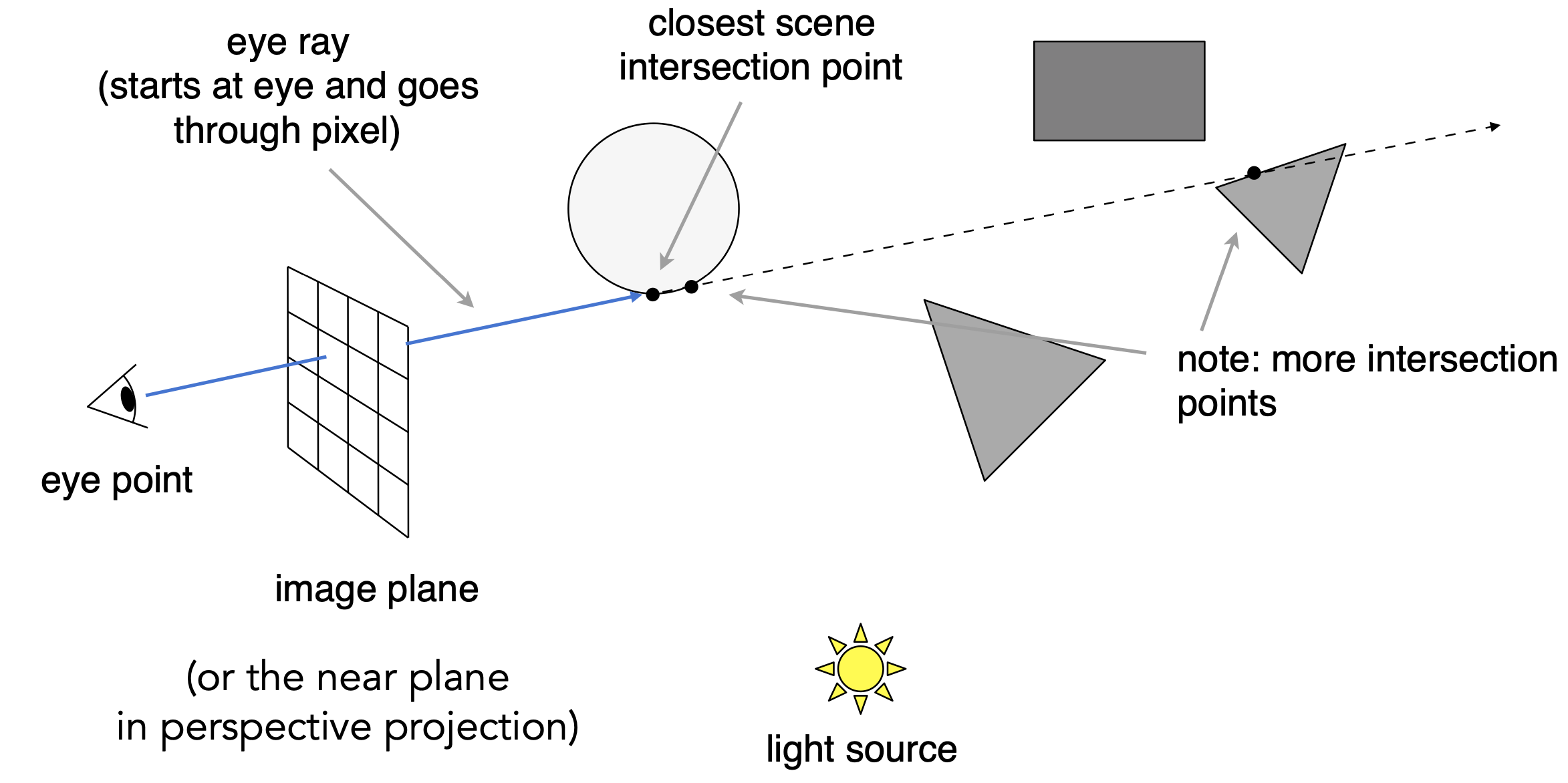
  - 对于光线和多个物体相交的情况：因遮挡，只考虑最近（直接避免光追中的深度测试）
- Step2: 交点与光源连线，若不在阴影中就计算着色
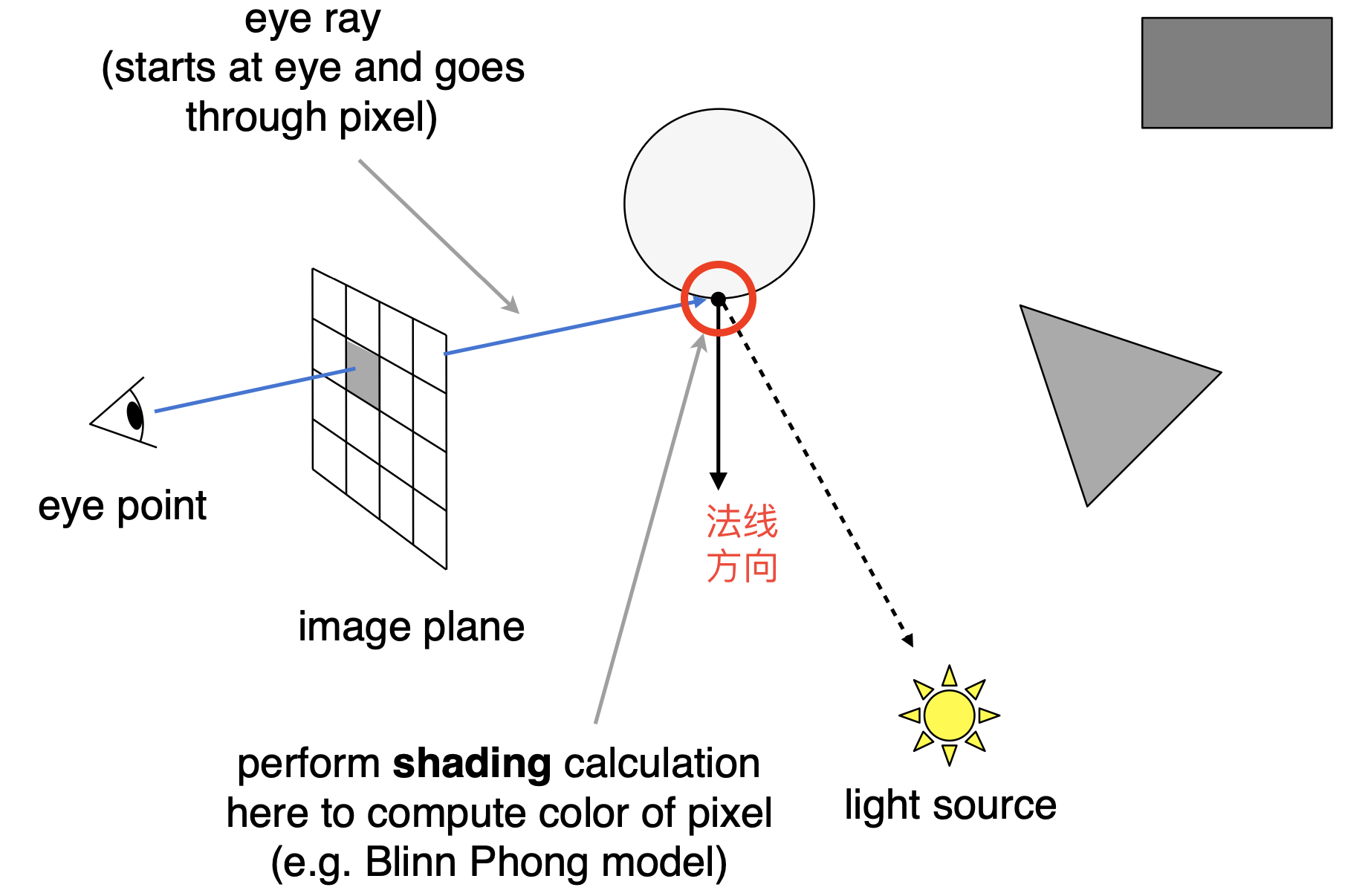
- Step3: 写入对应像素

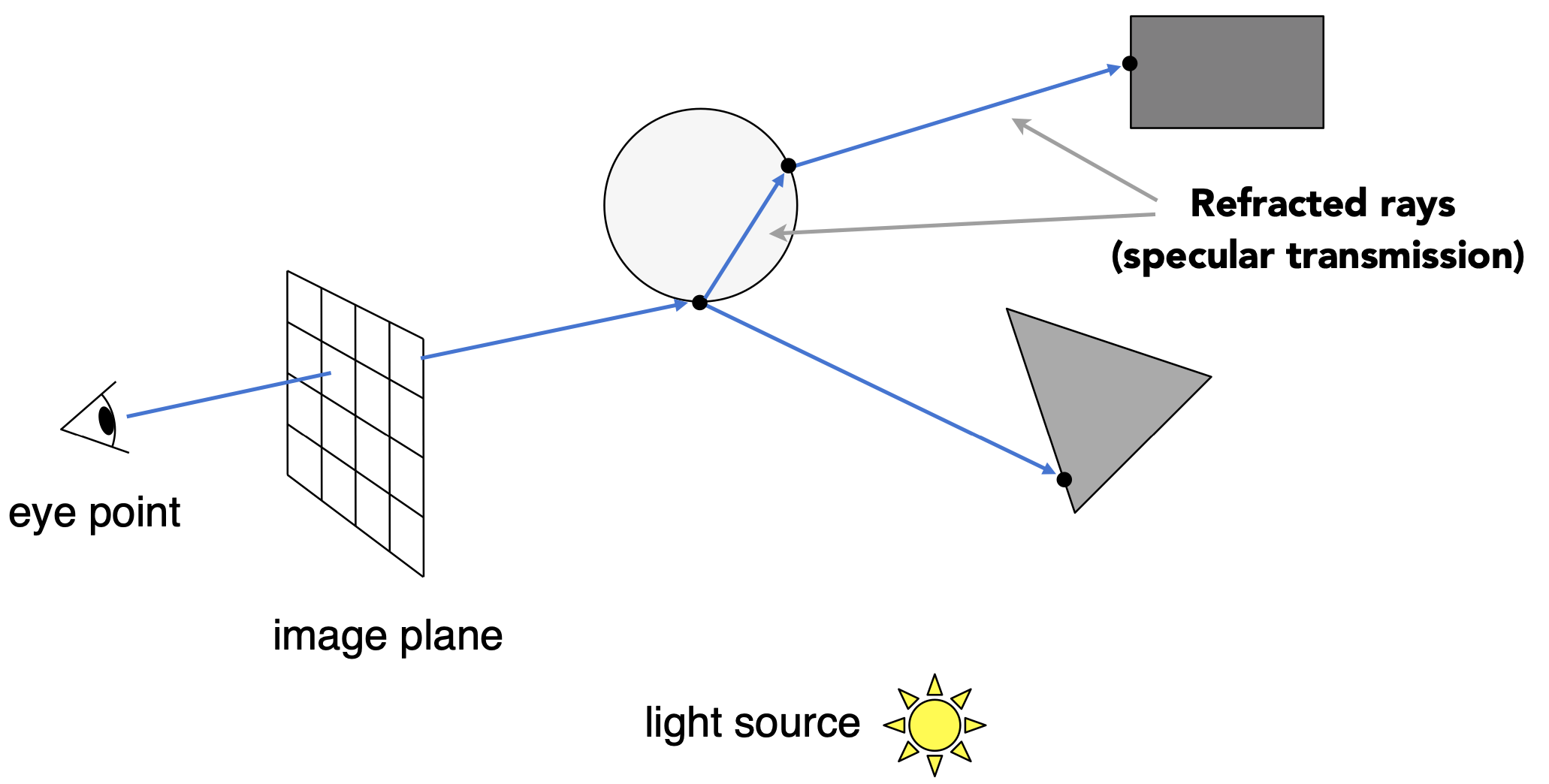
Recursive (Whitted-Style) Ray Tracing

截屏2023-04-24 10.09.39

对于透明物体，发生折射+反射
过程
- 生成眼睛到屏幕像素的primary ray
- 形成反射（镜面反射）or折射的多条secondary rays；若打到漫反射物体，反射/折射停止
- 作出shadow rays
- 若shadow rays未被物体遮挡，则计算对应红圈处的点的着色，相叠加，得出屏幕像素最终颜色

Ray-Surface Intersection 光线和面求交

光线和球体求交

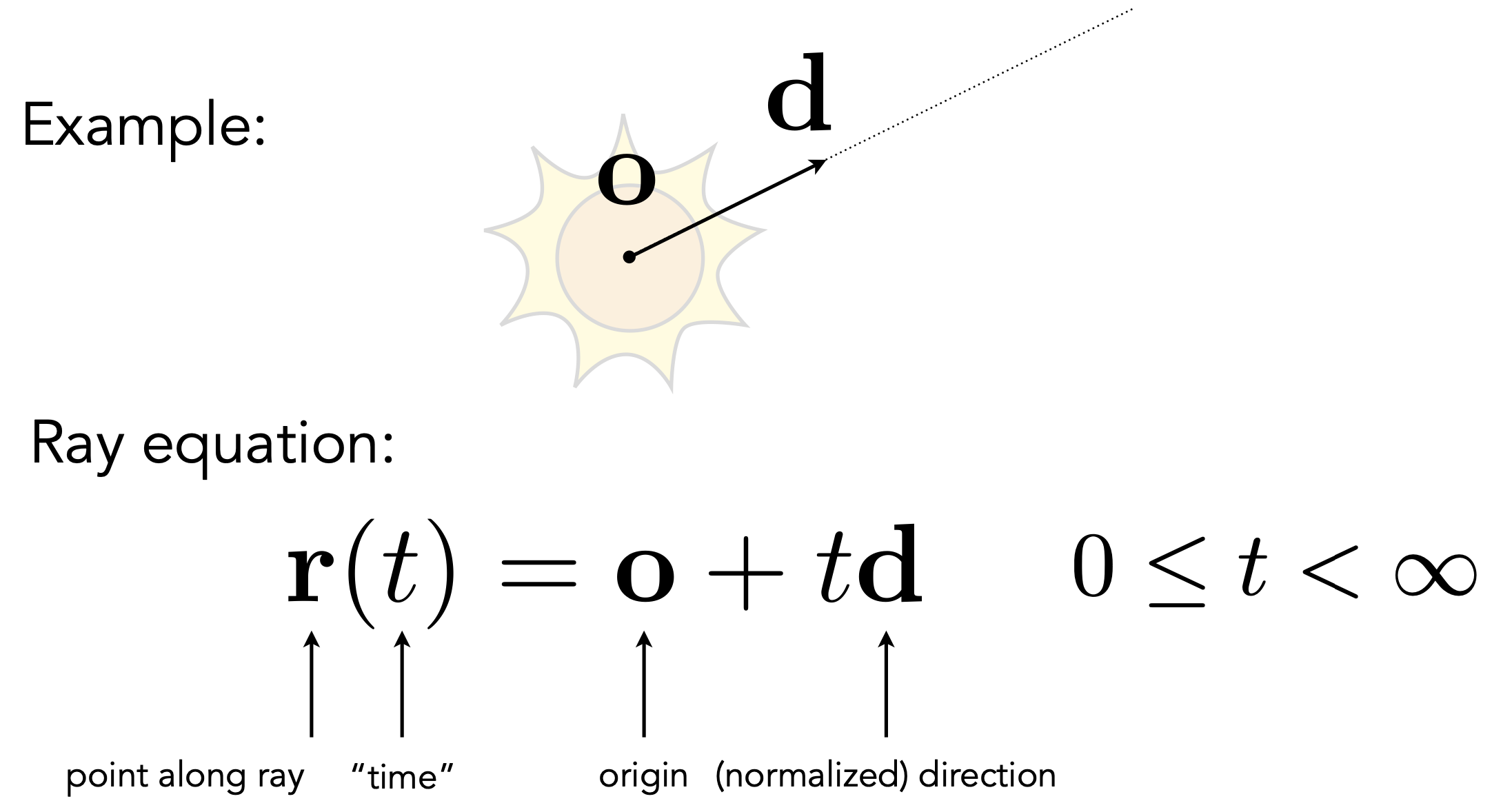
光线：起点+方向
联立方程求交点：
- 光线：$r(t) = \boldsymbol o+t \boldsymbol d , (0 \leq t < \infty)$
- 球：$\boldsymbol p: (\boldsymbol{p} -c)^2 - R^2 = 0$

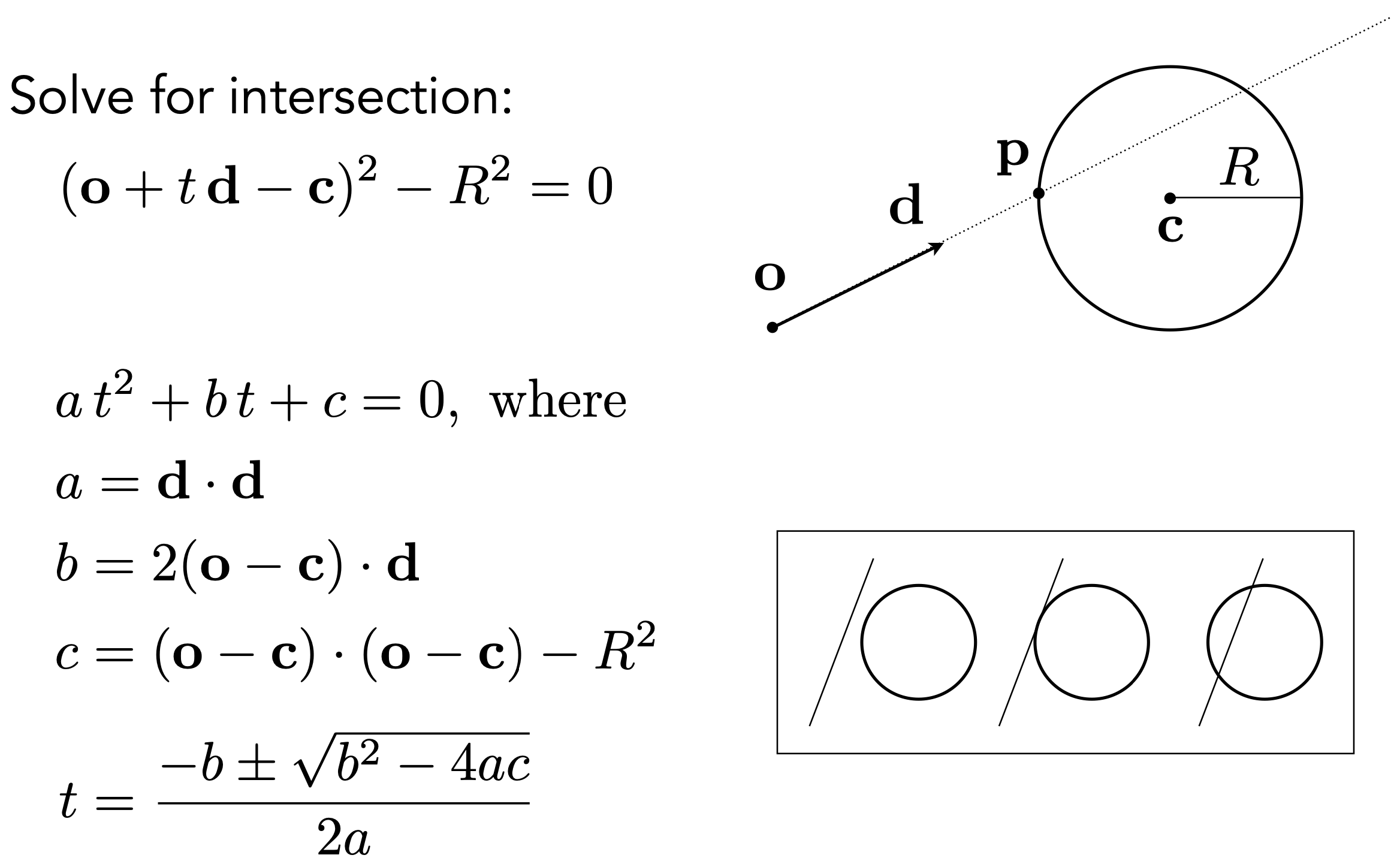
光线和隐式表面求交

将光线函数表示带入隐式表面公式

与三角面求交

截屏2023-04-24 13.49.32

补：判断空间中任意点是否在（封闭）物体内：
- 从该点向任意方向做一条光线，检测光线和该物体交点个数
- 若交点为奇数，则点在物体内；若交点为偶数，则点在物体外
光线与三角面求交计算过程
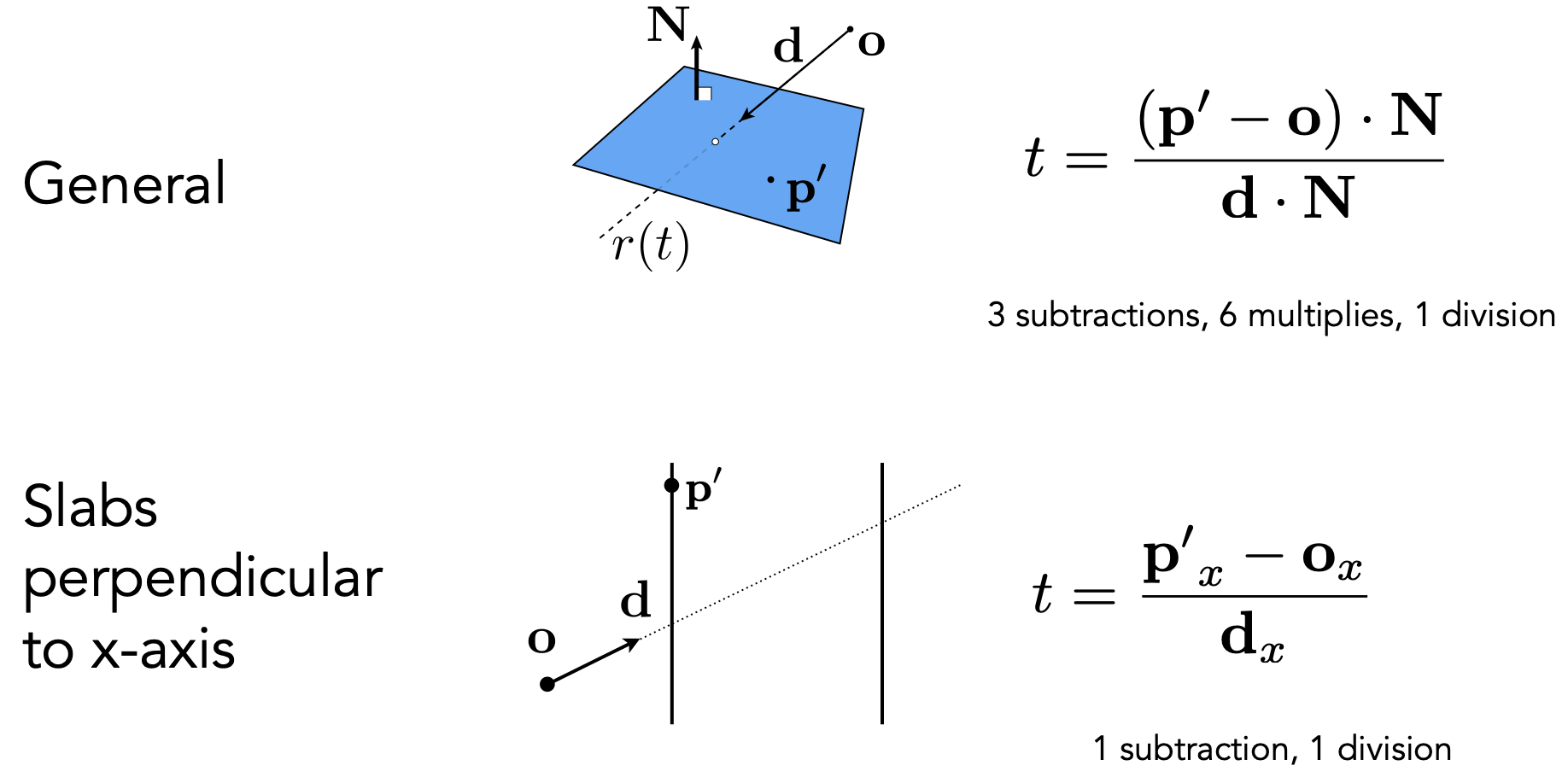
- 光线和三角形所在面求交
  - 平面的定义：法向量$\boldsymbol N$+一个点$p’$
  - 平面上的点$\boldsymbol p$和法线$\boldsymbol N$满足向量$\boldsymbol{p’p}\perp \boldsymbol N$，则点乘为0：
  - 联立光线&平面方程求交：
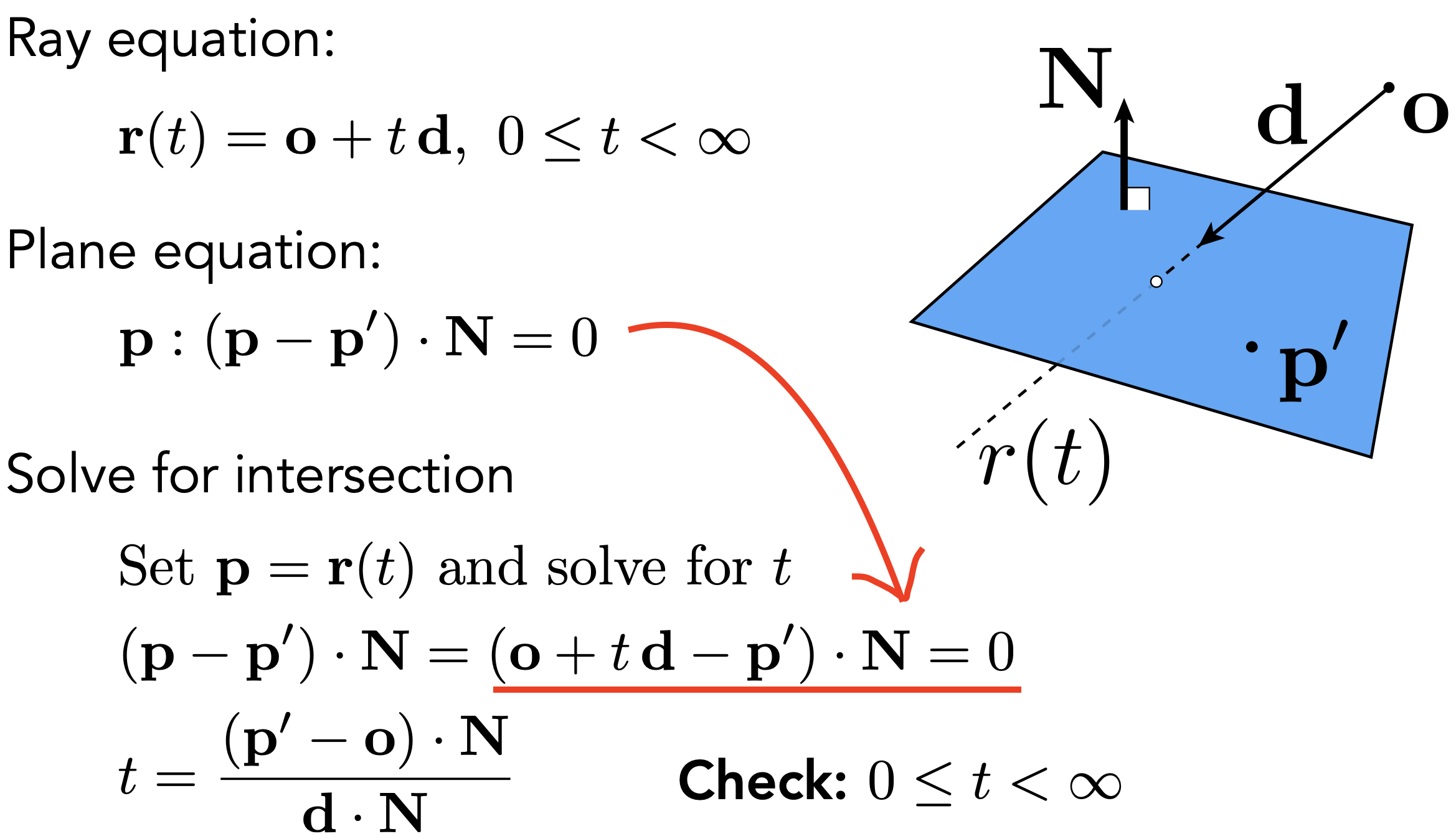
- 判断交点在不在三角形内（叉乘）
Möller Trumbore Algorithm：光线方程 = 重心坐标方程（可表示三角形平面内任意一点）

缺点问题

测试每一个三角形与光线的交点，找到最接近的交点（即最小t）
Naive algorithm = #pixels ⨉ # traingles，每一个像素都要遍历场景中所有三角面，慢

Accelerating Ray-Surface Intersection 加速

Ray Intersection with Axis-Aligned Box

Bounding Volumes 包围体积(盒)
- 思路：将复杂物体用简单物体包围，若光线不与包围盒相交，则肯定不会与物体相交
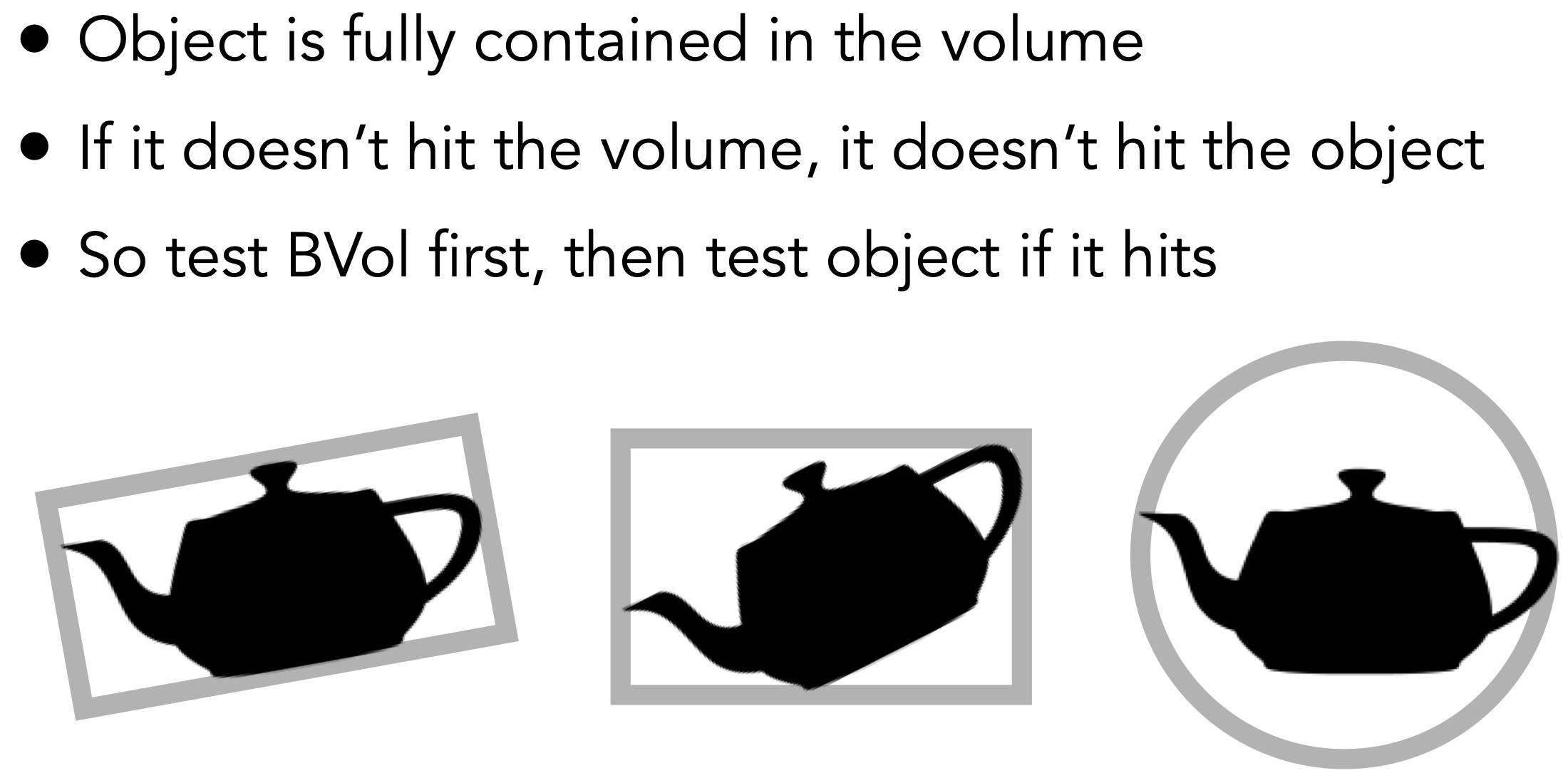
Axis-Aligned Bounding Box (AABB 轴对⻬包围盒)
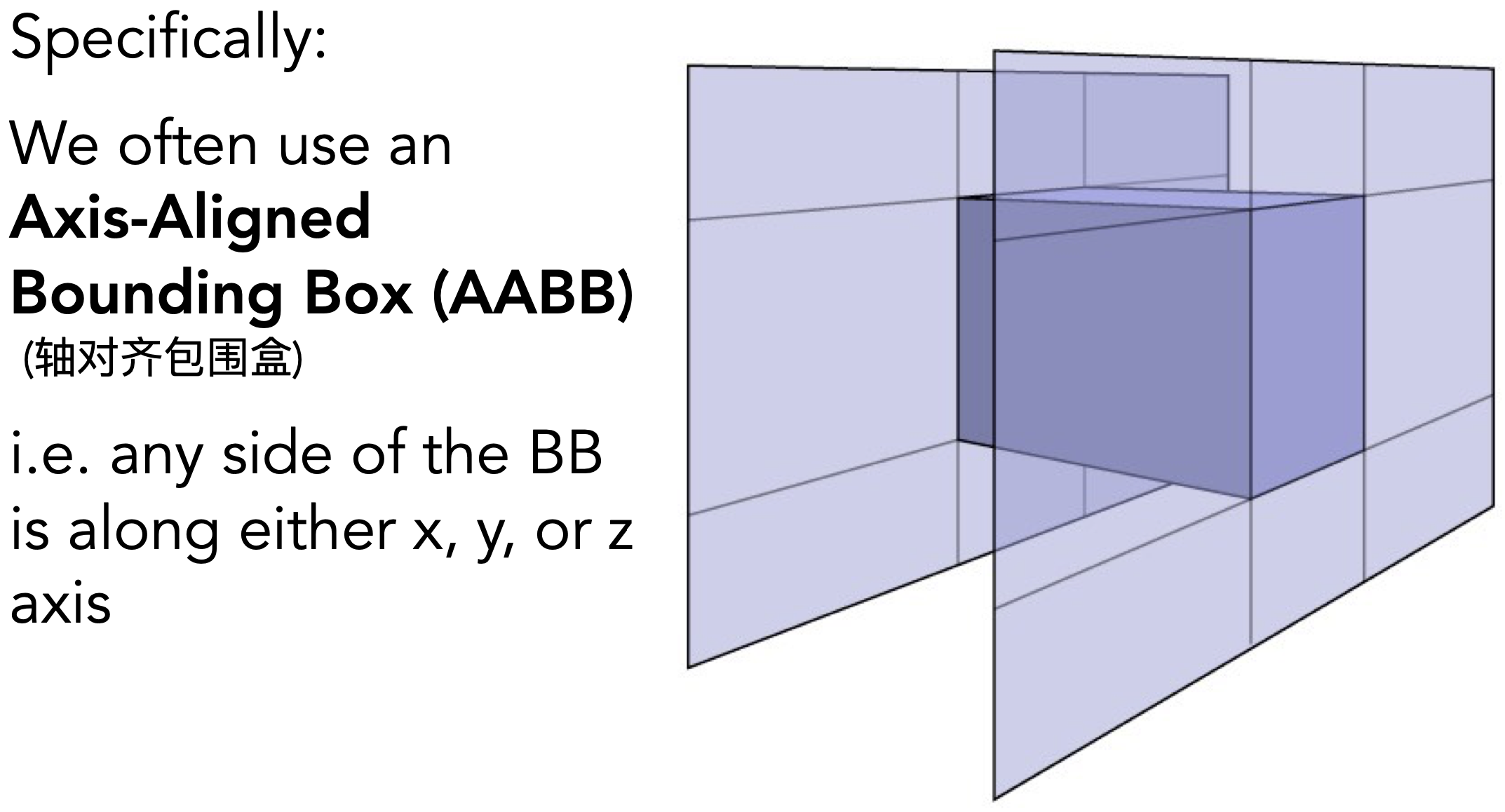
- 理解：三个对立面的交集
光线与AABB求交
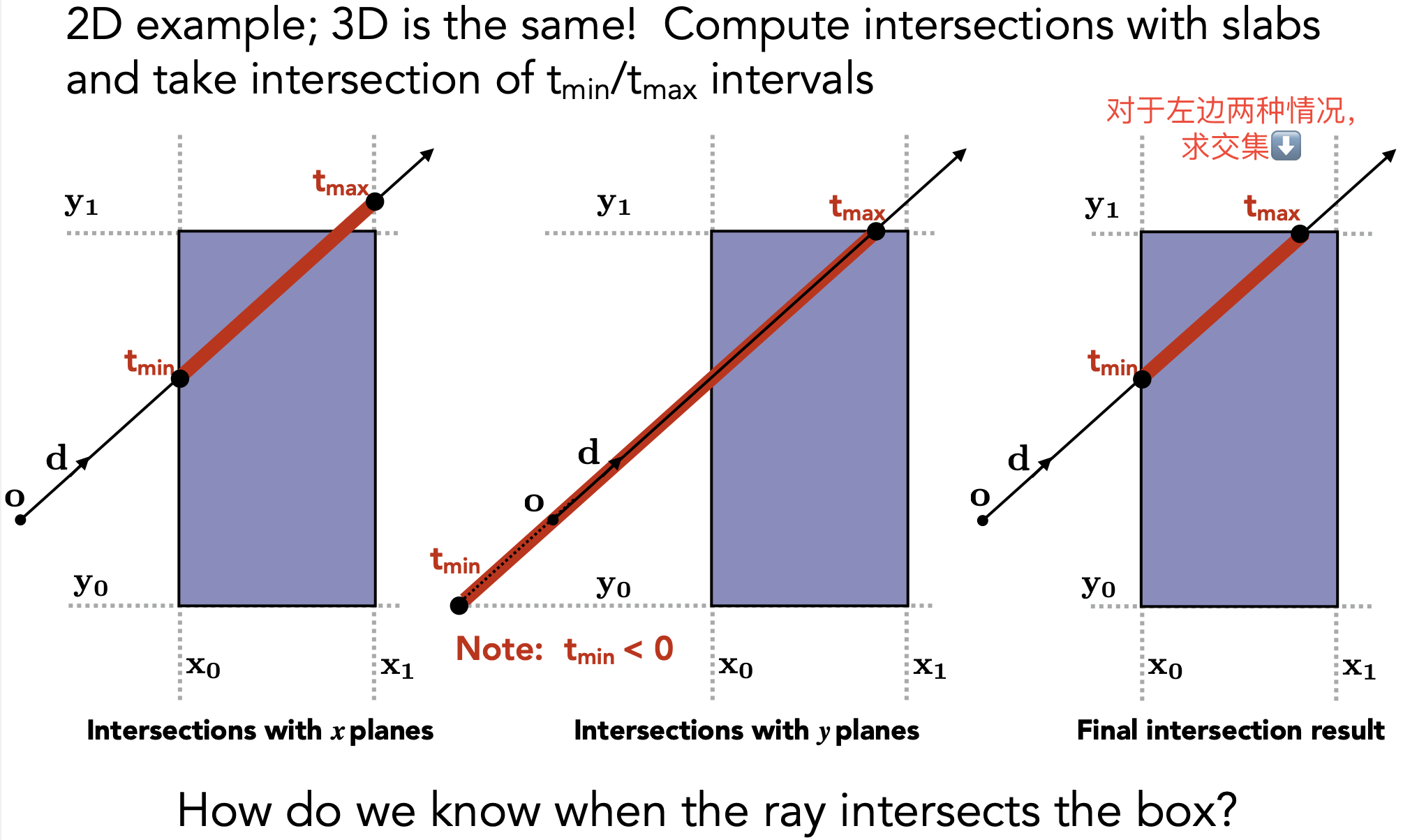
- Key Ideas
  - 光线射入AABB：光线射入所有对立面
  - 光线射出AABB：光线射出任意一个对立面
- 计算过程
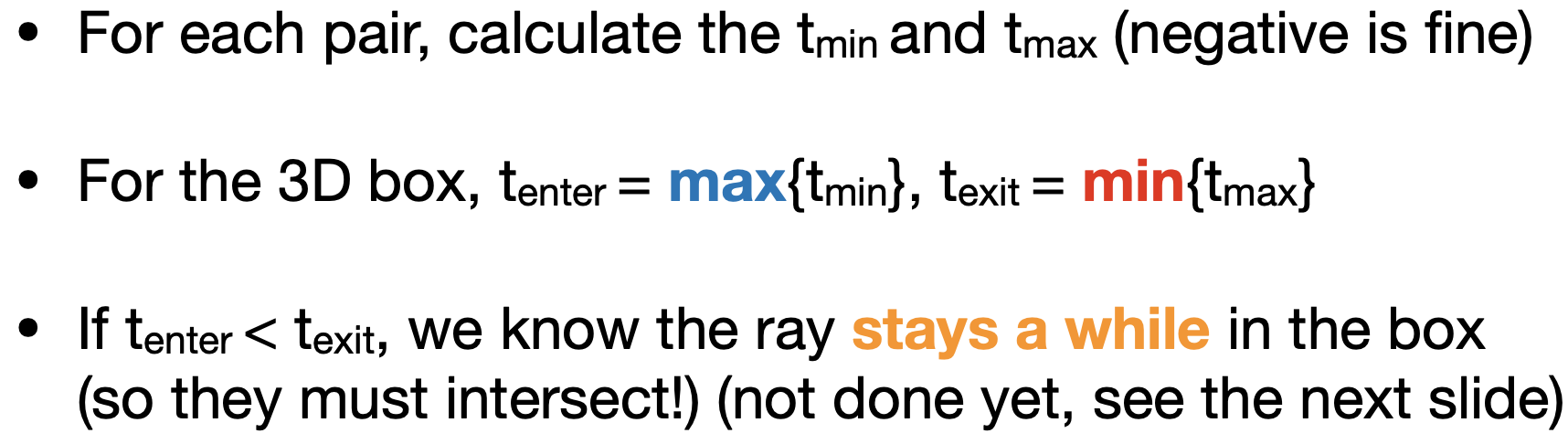
  - 有交点，当且仅当$t_{enter} < t_{exit}$ && $t_{exit} >= 0$
  - 若$t$为负
    - $t_{exit} < 0$：AABB在光线反方向，没有交点
    - $t_{enter} < 0$ && $t_{exit} >= 0$：光线起点在AABB里
Why Axis-Aligned? - 计算简单

P14&15 Ray Tracing 2&3 (Acceleration & Radiometry & BDRF & Probability)

Using AABBs to accelerate ray tracing

Uniform Spatial Partitions (Grids)

思路：将光线与物体求交换为光线与盒子求交
场景预处理
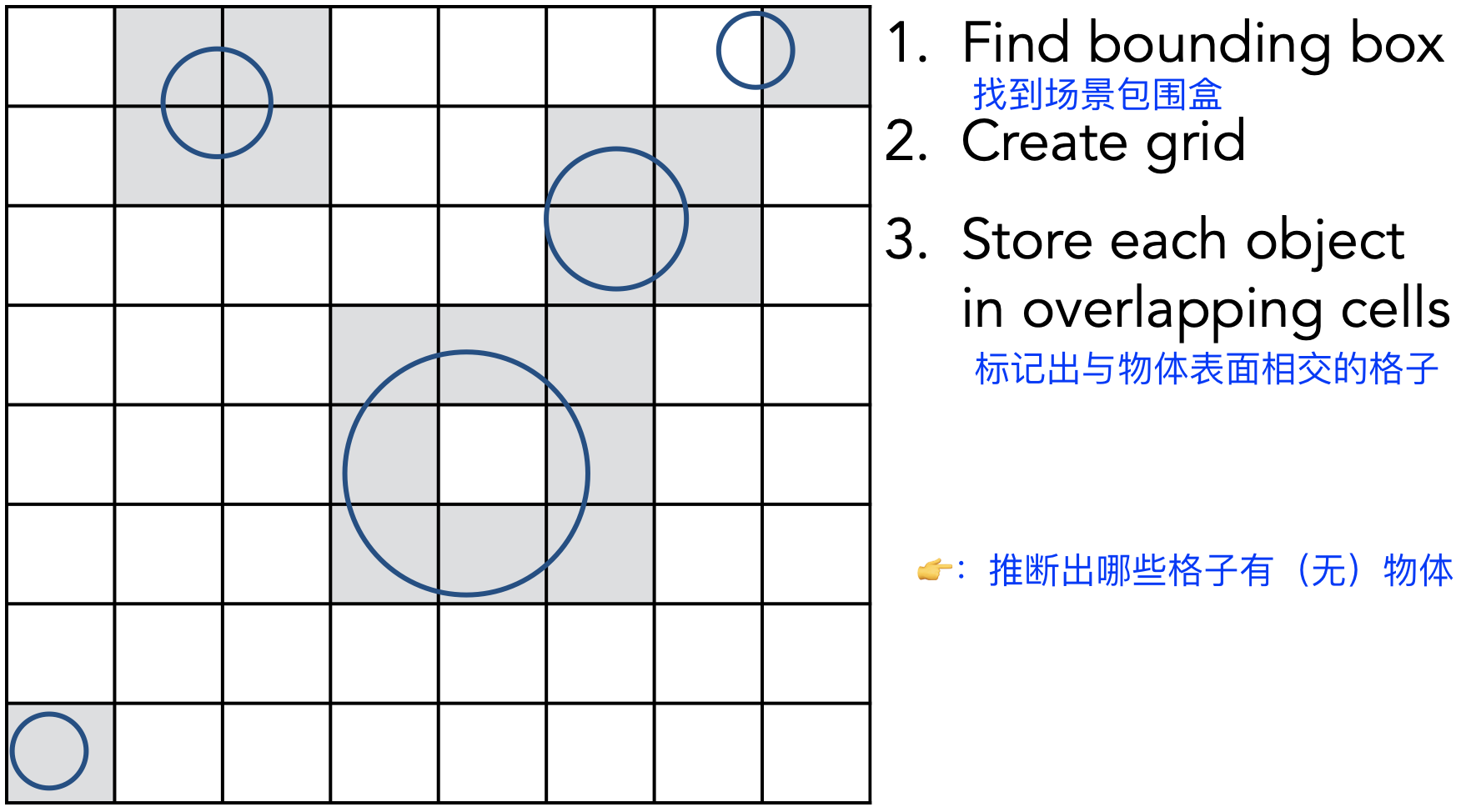
- 进行光线追踪
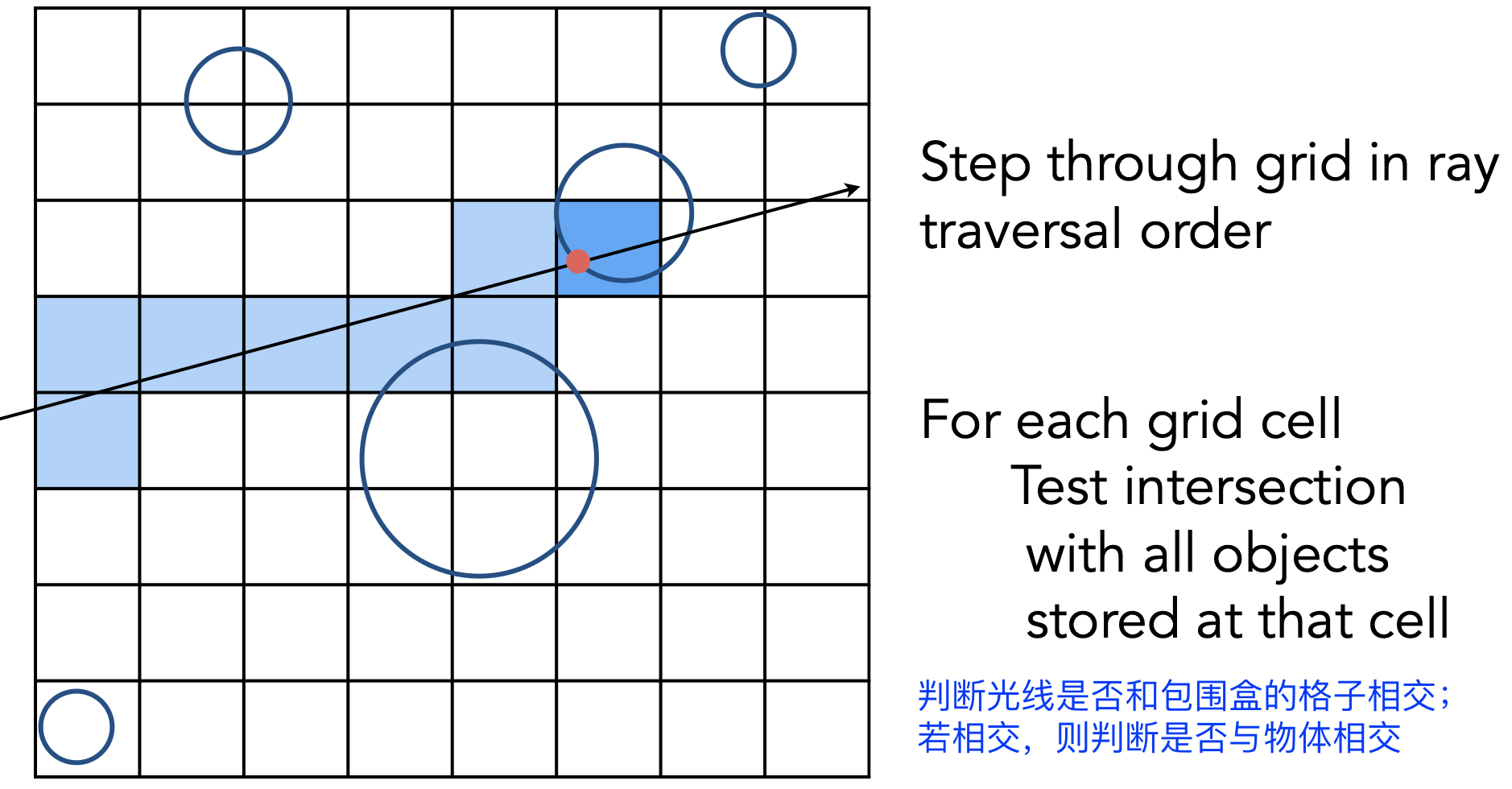
- 效率问题：寻找合适的格子数
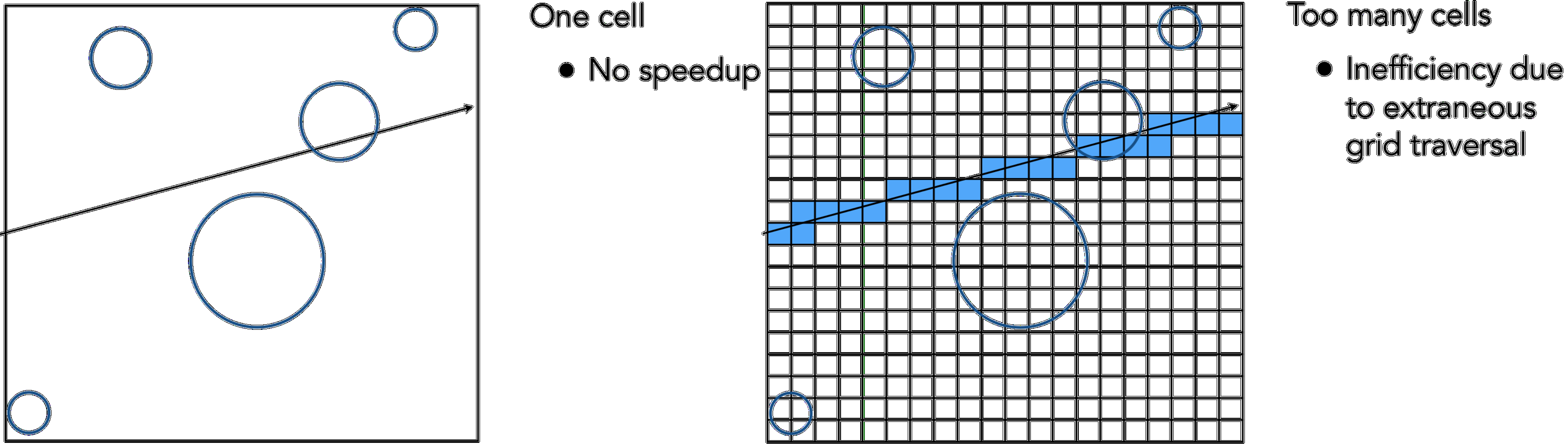
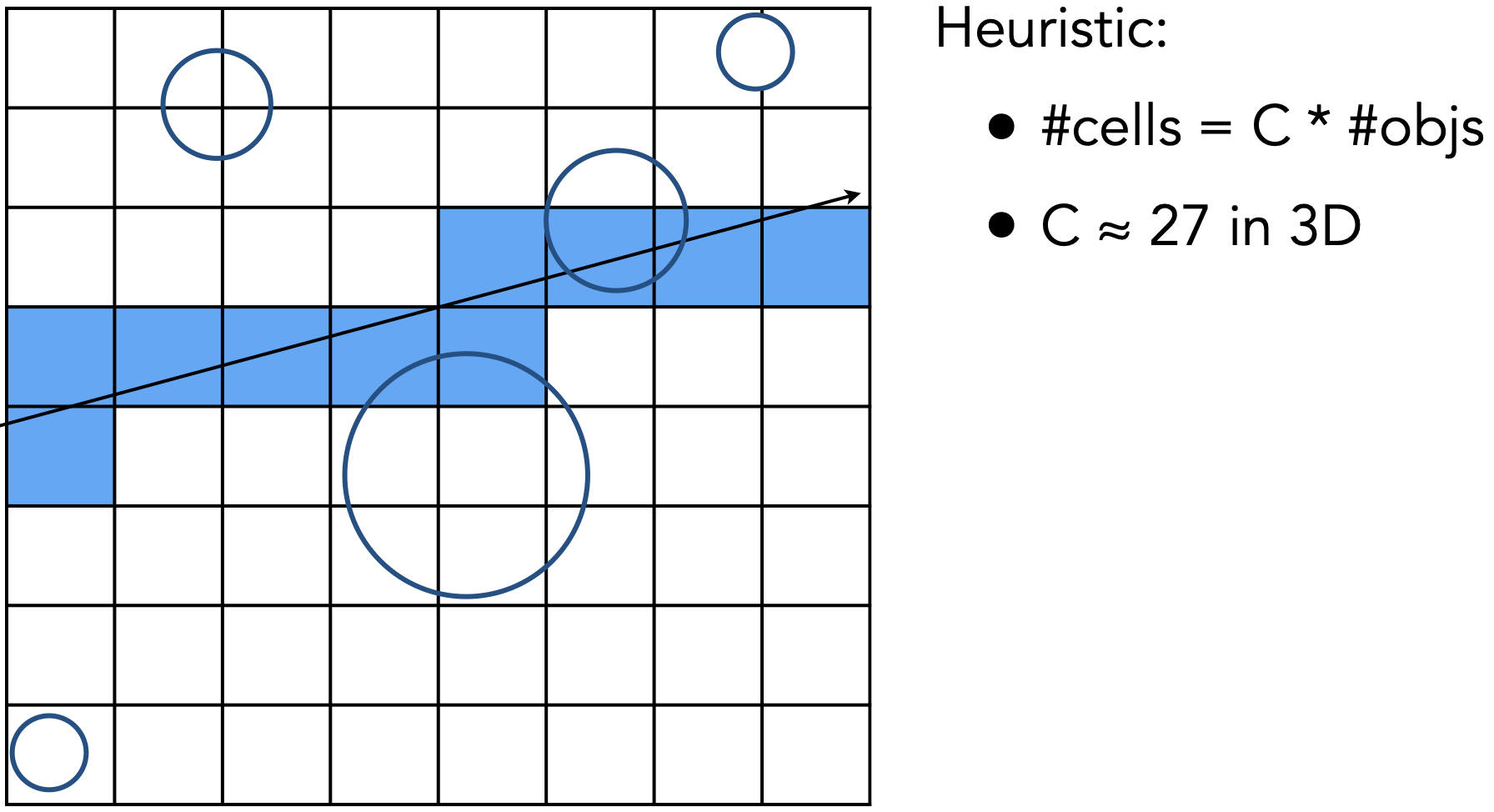
Grid可以很好地处理在大小和空间上均匀分布的大量对象集合，但是（问题）
- 不适用于物体分布不均的场景，会存在“Teapot in a stadium” problem。为检测小物体则需要密集的格子，浪费性能

Spatial Partitions 空间划分(光线追踪前)

解决物体分布不均导致的格子需求不同的问题
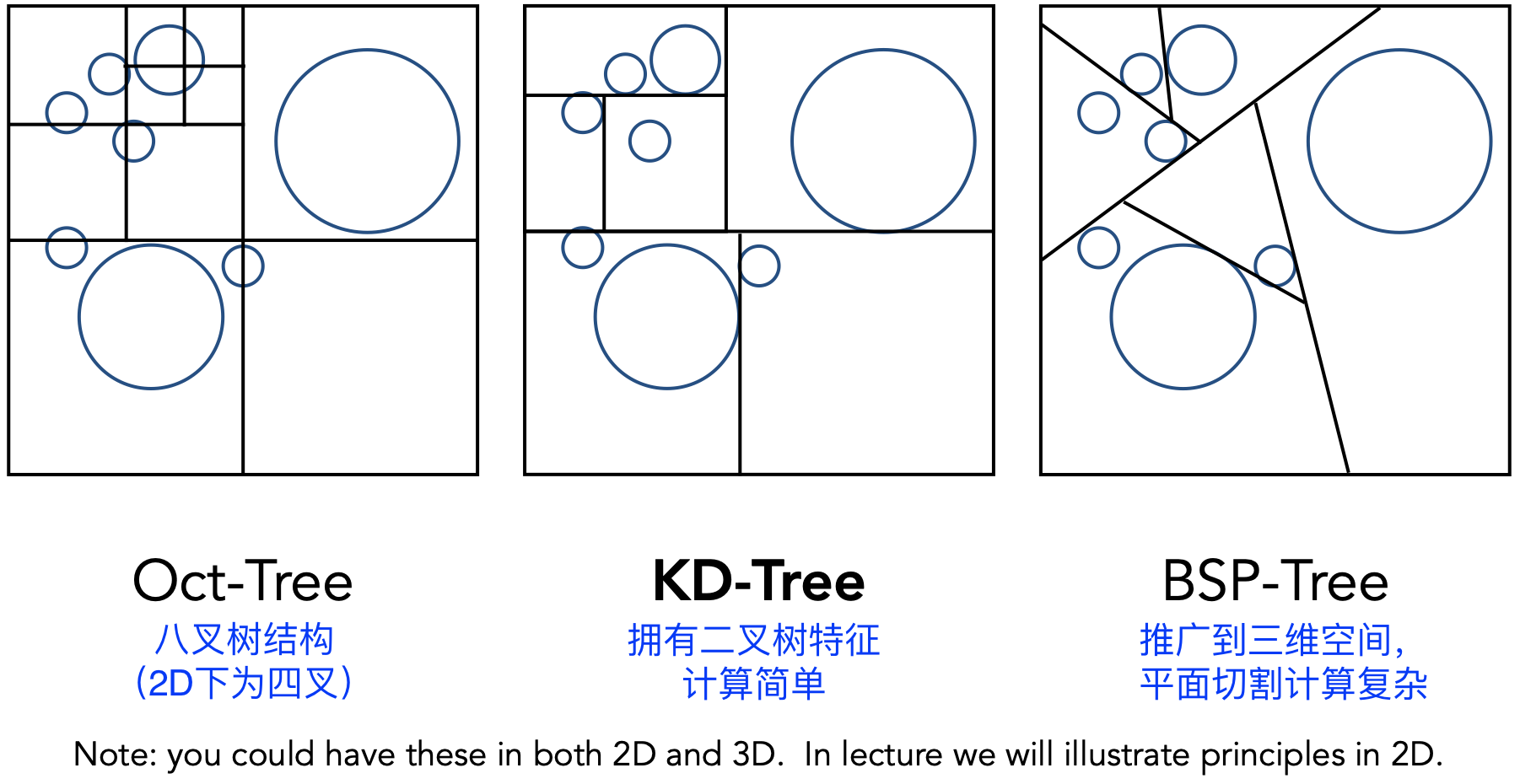
Spatial Partitioning Examples

KD-Trees

（加速构造都在光追前进行）

预处理：对空间进行划分，每个子空间每次只划分一次，横竖交替（1、2、3的划分在下图中省略）
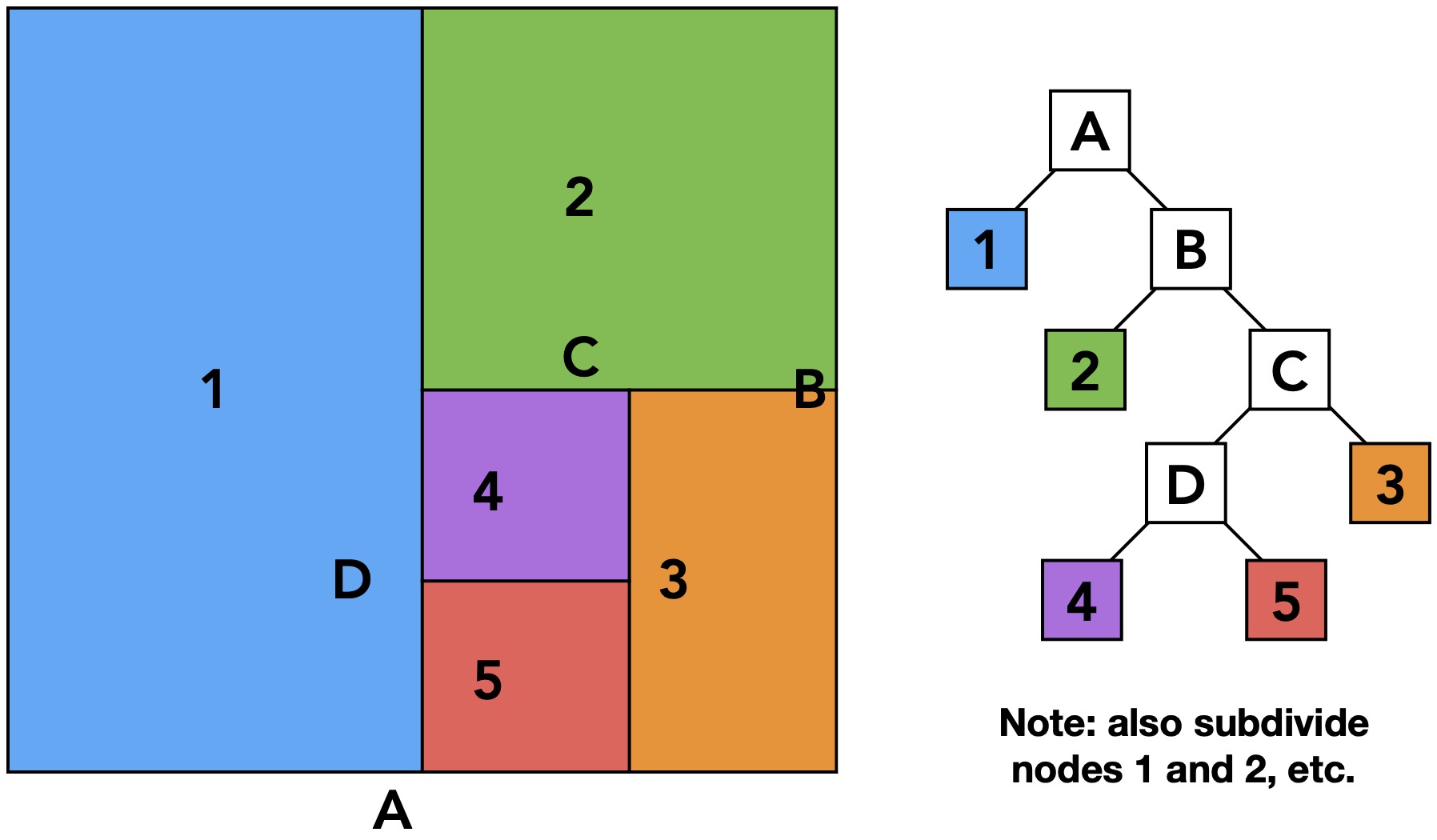
- 停止划分：划分出区域与光线无交点
KD-Trees的数据结构
- Internal nodes
  - 划分轴：x、y（三维还有z轴）
  - 分割的位置：平面上沿轴，具体规则还需计算
  - 子节点的指针
  - 不存储objects（与grid相交的三角形）
- Leaf nodes：存储objects
计算过程（思路：判断光线是否与格子有交点，若无，则无后续操作；若有，则光线可能与其子节点有交点，继续划分，直到打到叶子节点，若有交点，再与叶子节点中所有三角面求交）
- Step1：判断光线与包围盒A相交，需对A划分
- STEP2：针对划分后A。判断光线与叶子节点1相交（这里把1、2、3看成叶子节点），则光线与1中所有object求交；判断光线与B相交，需对B划分
- STEP3：针对划分后B。判断光线与叶子节点2相交，则光线与2中所有object求交；判断光线与C相交，需对C划分
- STEP4：针对划分后C。判断光线与叶子节点3相交，则光线与3中所有object求交，这里有交点，记录$t_{hit}$；判断光线与D相交，需对D划分。
- ……
- （判断光线与5无相交，则无须再求交并划
缺点
- 预处理阶段，三角面与网格求交难。如三维网格题穿过三角面内部，计算结果却为无交点
- 同一个object可存储在多个叶子节点中（？）
补：KD-Trees缺点难解决，不怎么用了

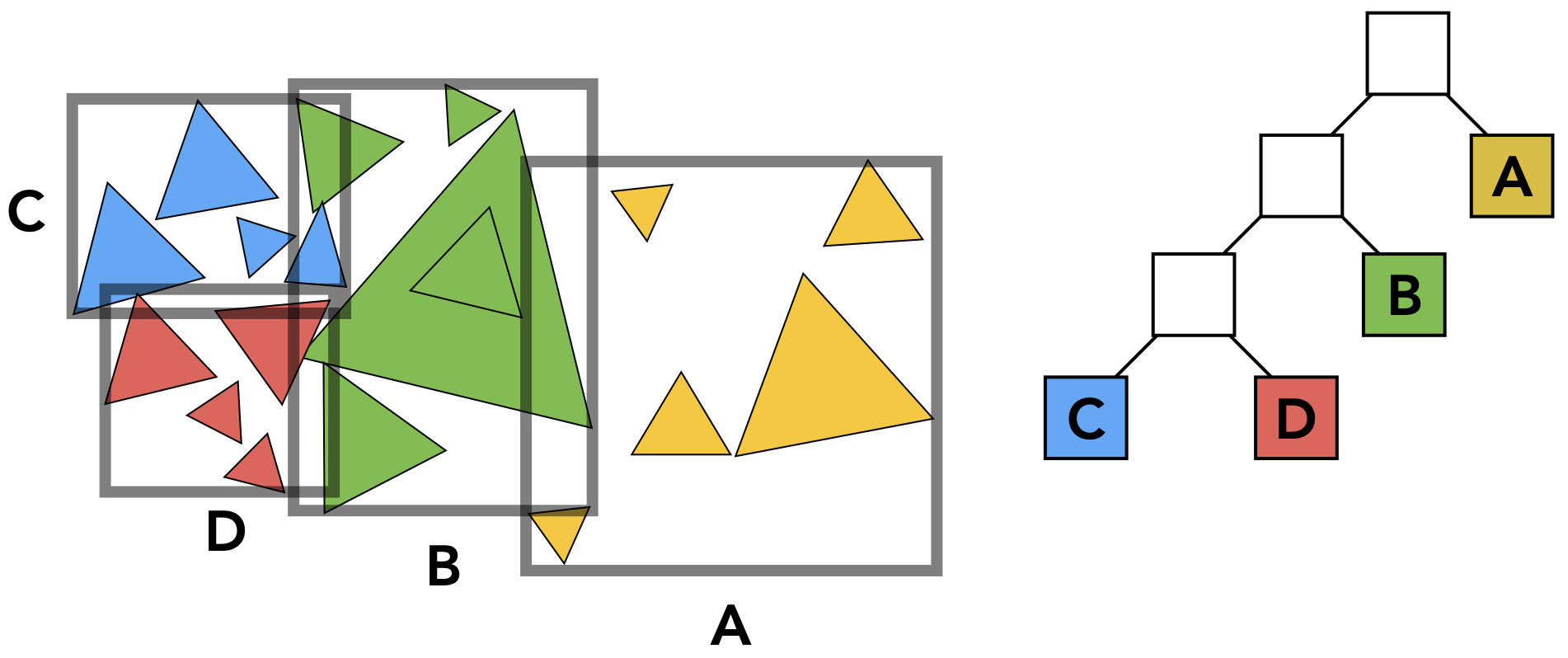
Bounding Volume Hierarchy (BVH)

（Kind of Object Partitions 一种物体划分，计算简单且效率高，应用更广泛）

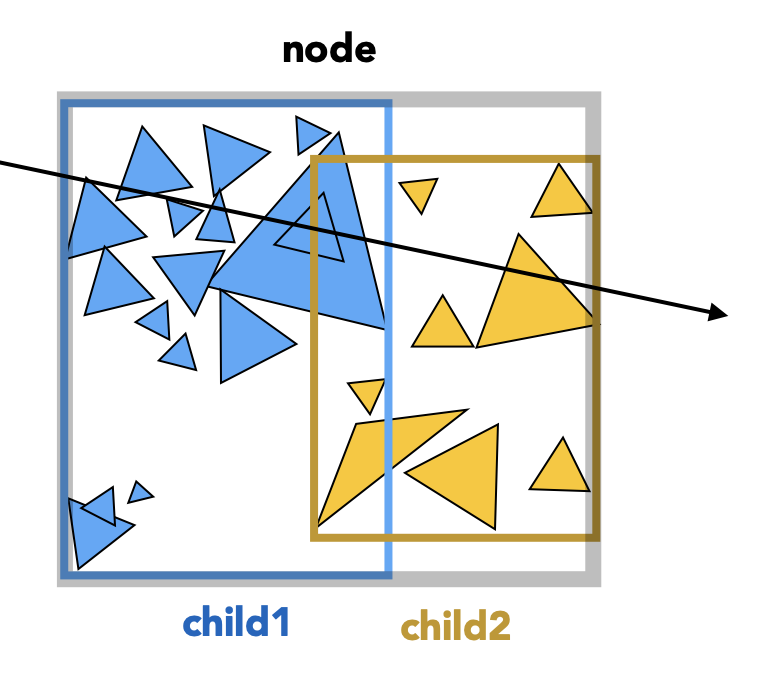
思路
- 将空间中三角形分成两部分，并重计算包围盒
- 继续进行两部分的划分，停止条件根据规定or自设
特征
- 优点：解决KD-Trees缺点，一个object只会出现在一个格子里
- 缺点：包围盒有相交，存在空间冗余
过程
- 计算包围盒
- 递归地，将一个包围盒分成两部分，并同步将其内部objects也分成两部分
- 重新计算两部分的包围盒
- Stop when necessary
- 实际物体记录在叶子节点，其他节点只用于做加速结构的划分判断
如何划分
- xyz选择一个维度
- 技巧
  1. 选择最长的axis进行划分
  2. 选择中间位置的object进行划分，确保两部分object数量接近平衡（快速排序，补数据结构）
- stop when node contains few elements
BVHs的数据结构
- Internal nodes store
  - Bounding box
  - 子节点的指针，不存储objects
- Leaf nodes store
  - Bounding box
  - List of objects

计算光线与BVH相交的过程

Intersect(Ray ray, BVH node)
{
	if (ray misses node.bbox) return;
  
  if (node is a leaf node)
     test intersection with all objs;
     return closest intersection;
  
  // 递归
	hit1 = Intersect(ray, node.child1); 
  hit2 = Intersect(ray, node.child2);
  
  return the closer of hit1, hit2;
}

Spatial vs Object Partitions
- Spatial partition (e.g.KD-tree)
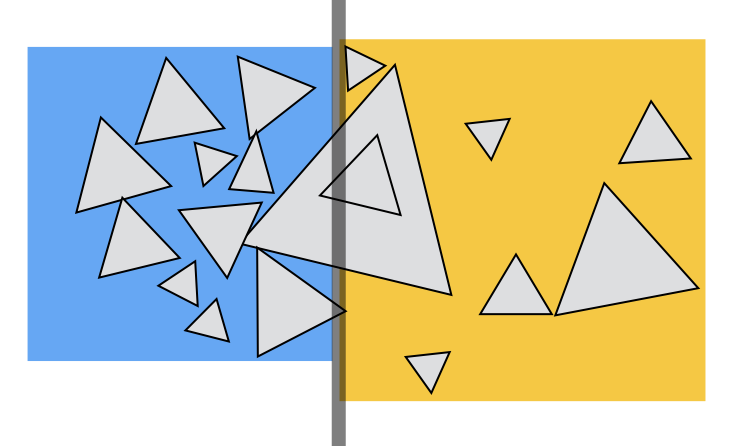
  - 划分区域在空间上不相交
  - 一个object可能被划分进多个子节点
- Object partition (e.g. BVH)
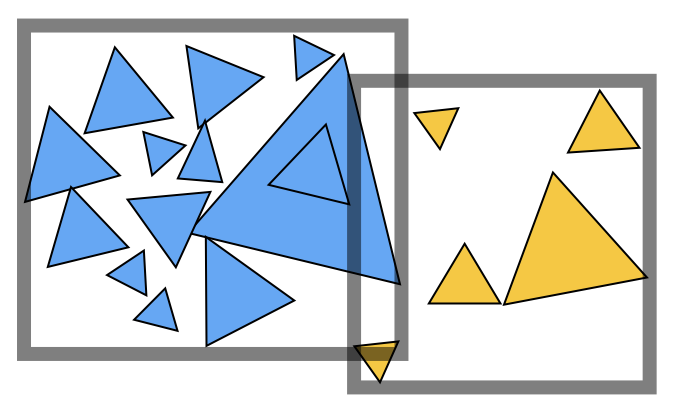
  - Bounding box在空间上可能重叠
  - object不会出现在多个包围盒中，也不用计算object和包围盒如何相交

Basic radiometry 辐射度量学

（Whitted style ray tracing 并不是真实的基于物理的结果，引入了大量的完美假设，同时有很多错误的估计。而辐射度量学是精确的定义光线与物体的交互，进行真实的物理模拟。）

Radiometry

新的概念：Radiant flux(power) 辐射通量 / intensity强度 / irradiance照度 / radiance

Radiant Energy $Q$ and Flux(Power) $\Phi$

Radiant energy $Q$：辐射能，是电磁辐射的能量，辐射通量对时间的积分。单位 $J$ 焦耳
Radiant flux(power)：辐射通量or功率，是单位时间内释放、反射、投射或吸收的能量，简单理解可认为该值说明一个光源有多亮。单位流明$lm$ / 瓦特$W$。计算公式：$\Phi = \frac{dQ}{dt}$
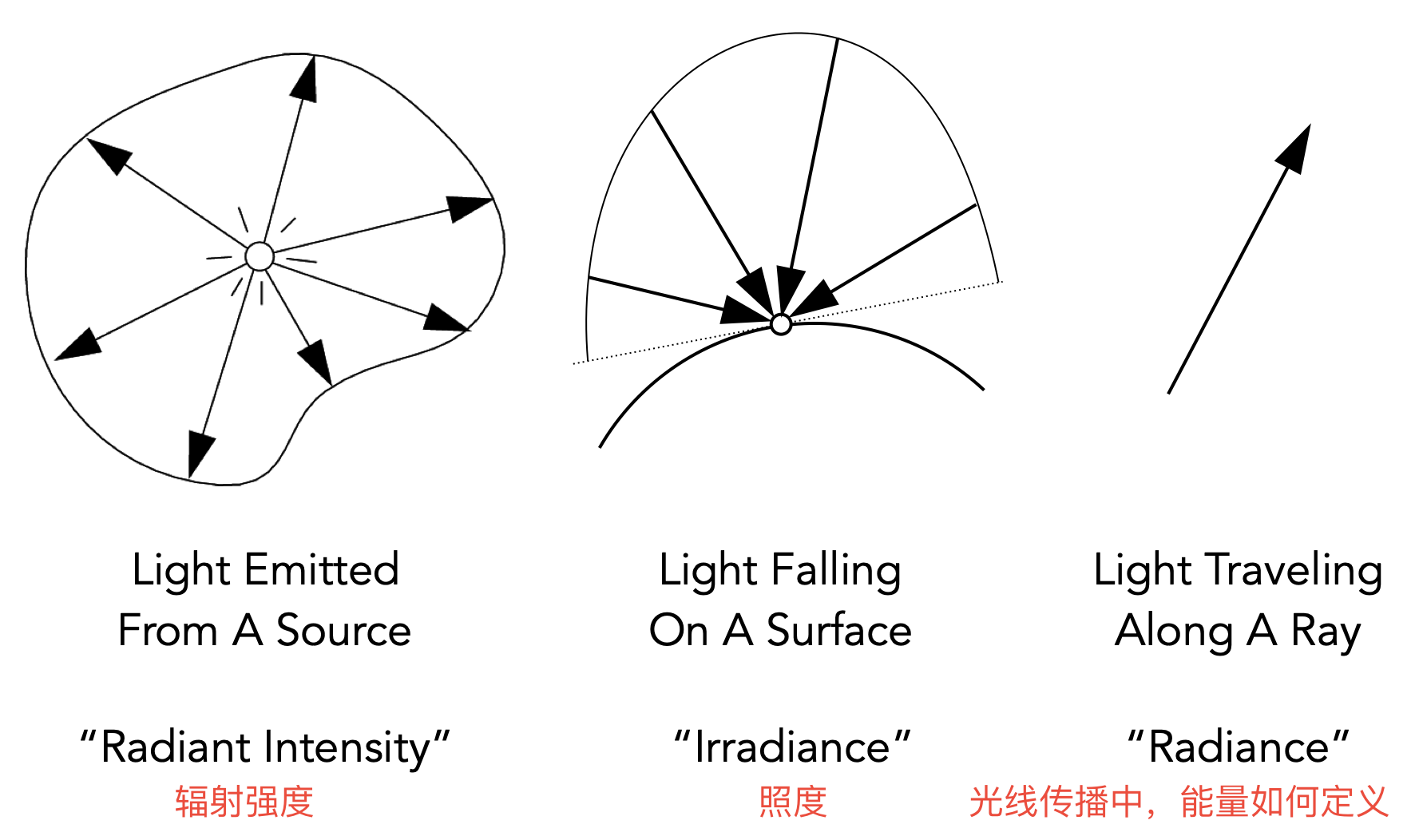
Important Light Measurements of Interest

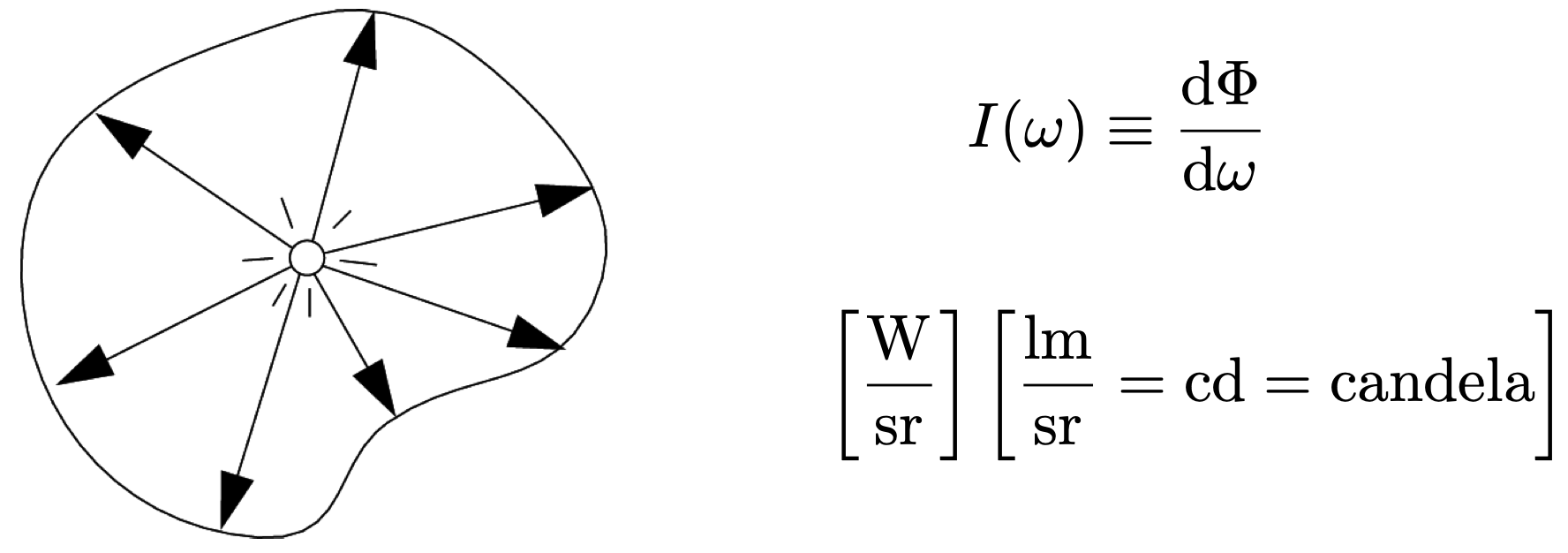
Intensity $I$

Intensity：辐射强度，单位立体角所包含的辐射通量/功率(针对立体角的方向上)。单位是 $cd$ 坎德拉

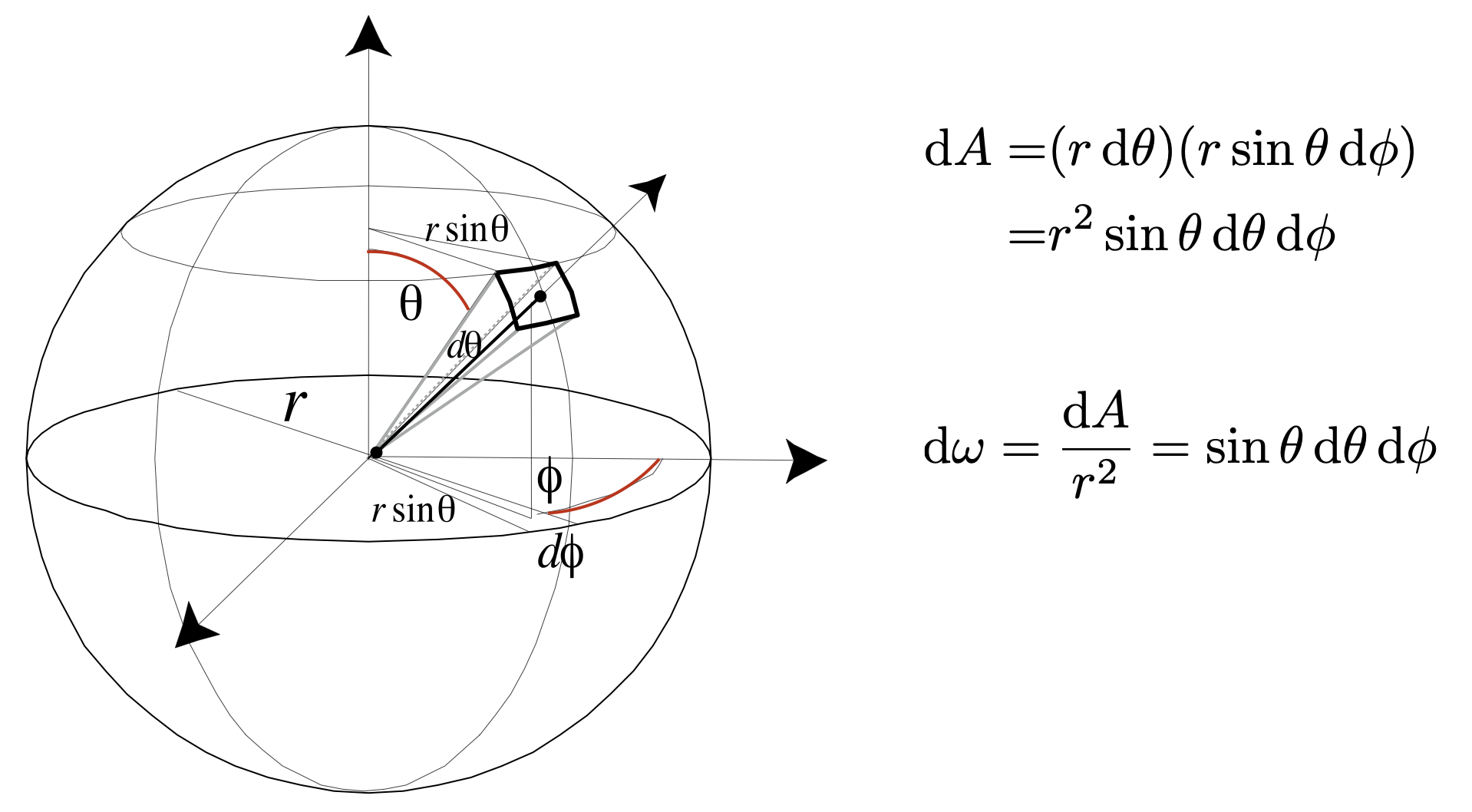
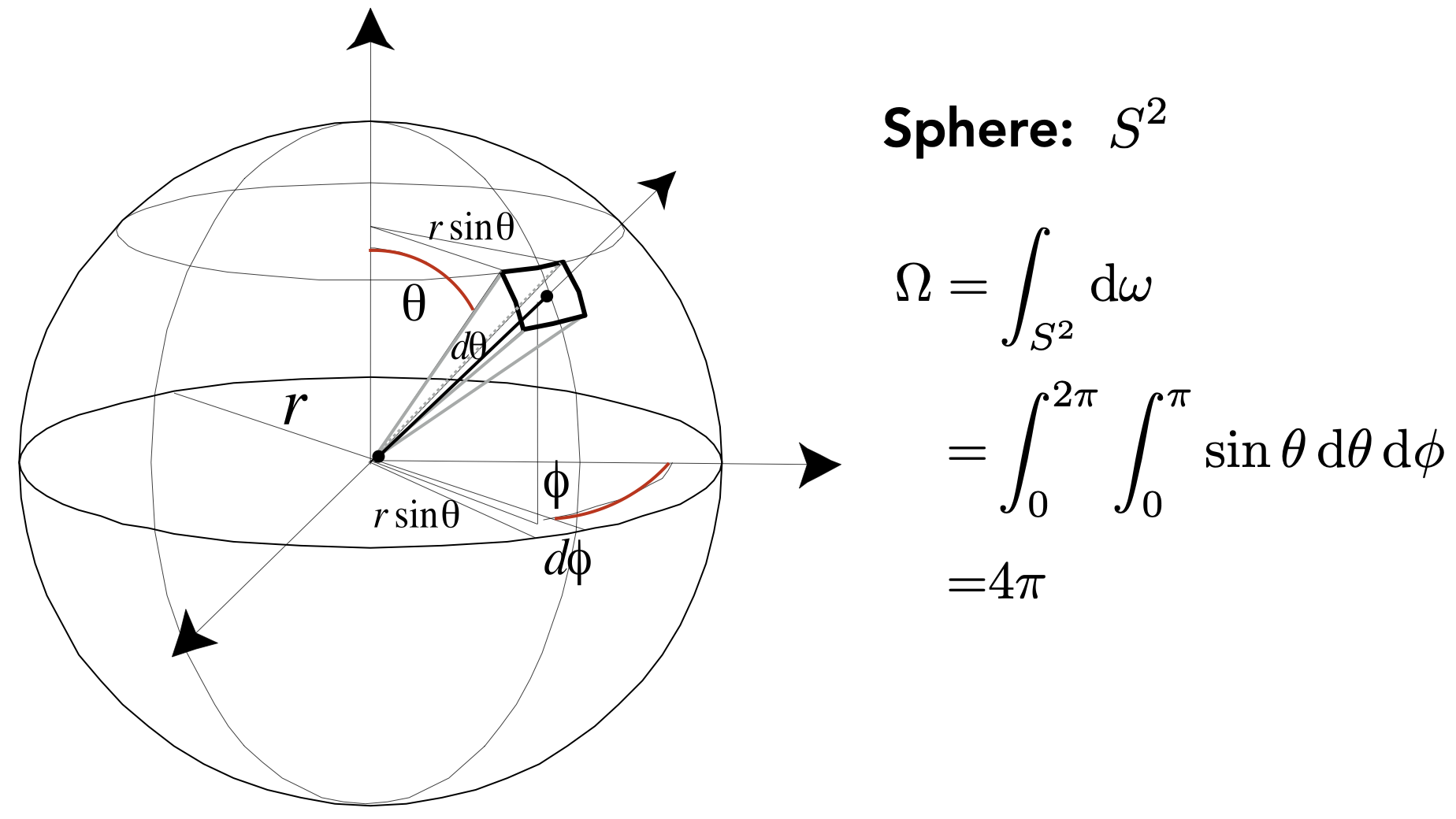
Angles and Solid Angles 立体角

单位立体角定义：在半径 $r$ 的球面上面积为 $r^2$ 的面元对球心的张角为 $1sr$ ，因为球面的面积是 $4 \pi r^2$ ，所以整个球面的立体角为 $4\pi sr$
立体角
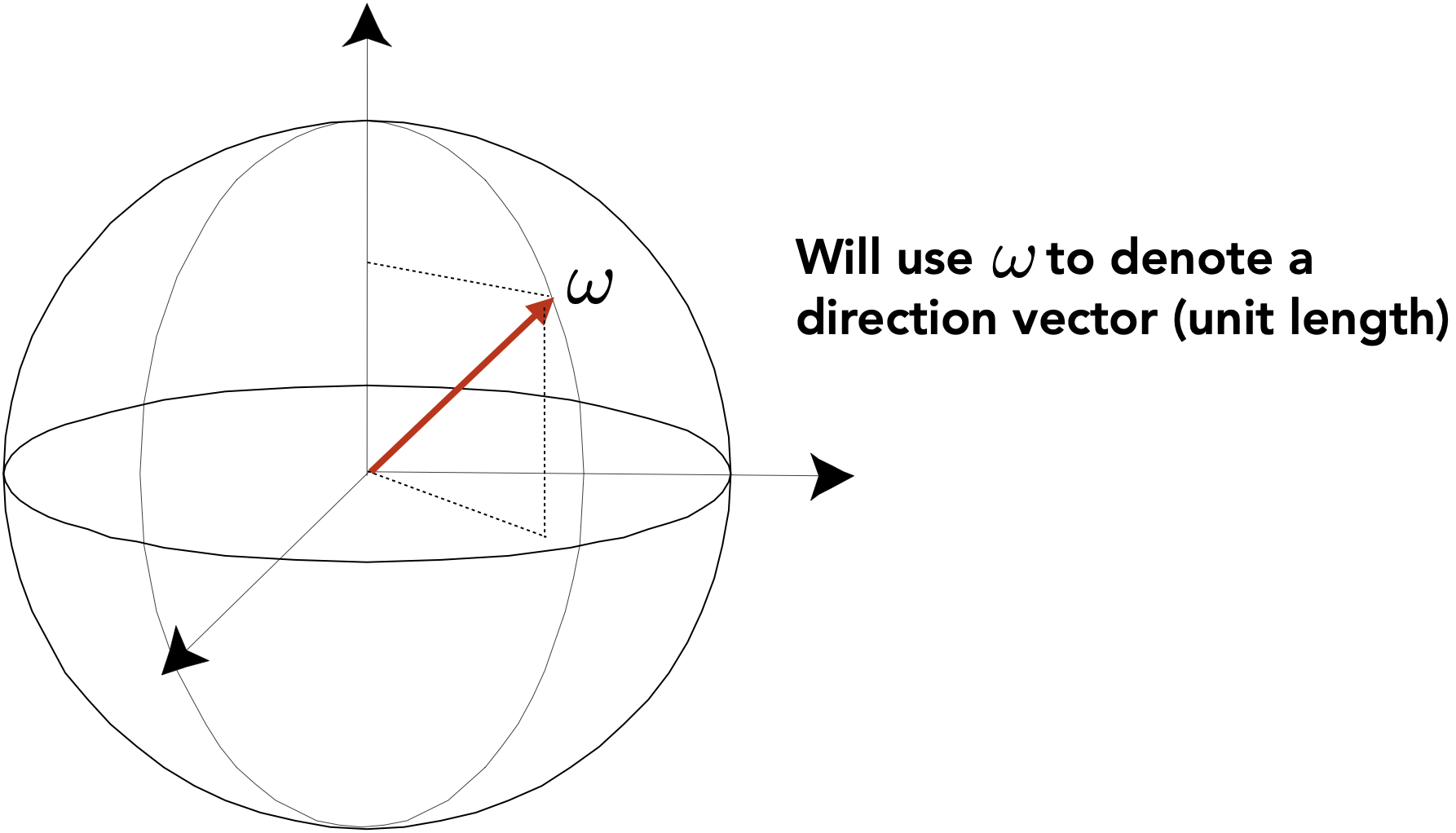
辐射度量学中， $\omega$ 通常被用来表示三维空间中方向，由 $\theta$ 和 $\phi$ 来表示具体方向，并可进一步计算出单位立体角
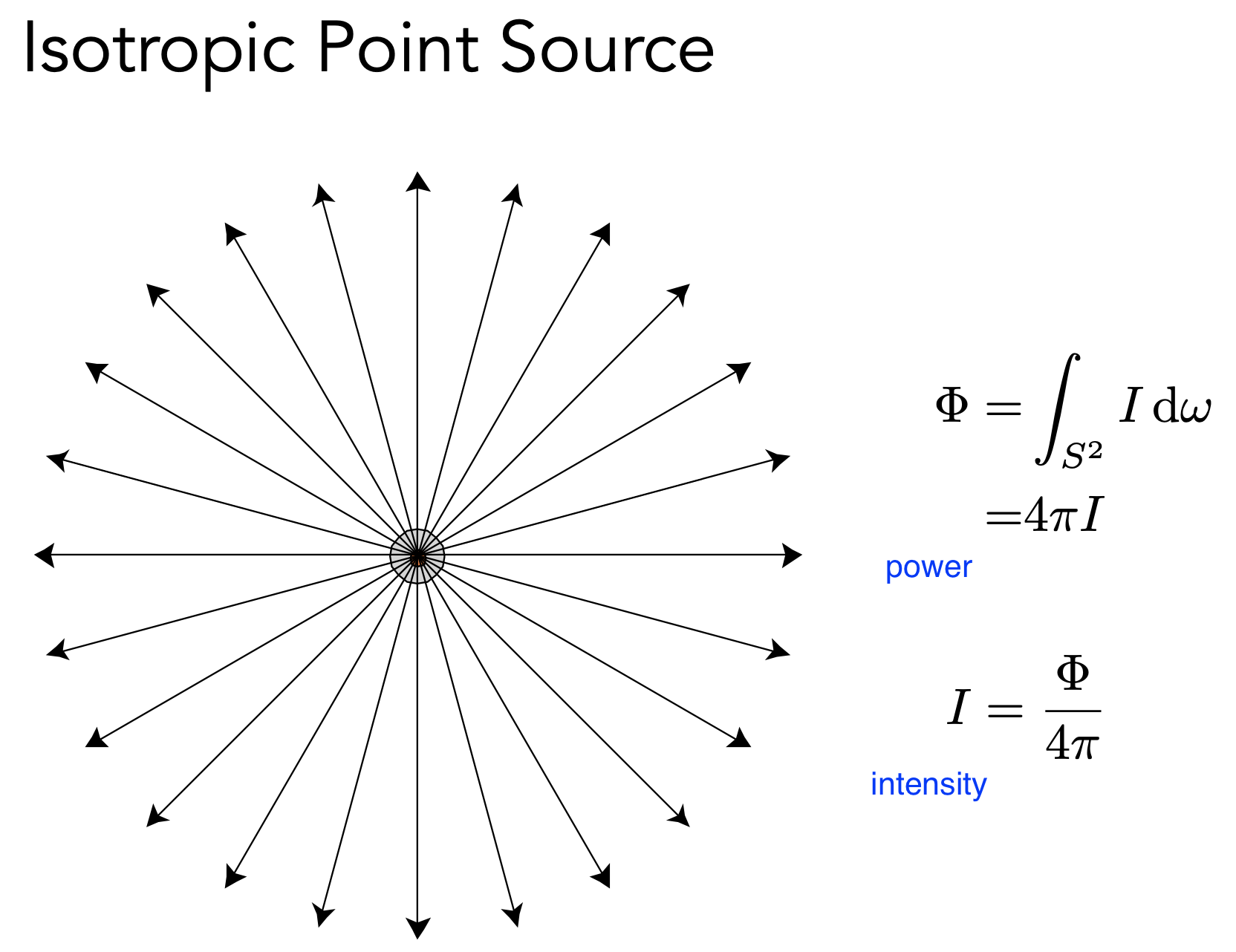
若空间中点光源，向四周均匀辐射能量，则辐射强度 $I$ 计算如下

Irradiance $E$

Irradiance：辐照度，power per unit area incident on a surface point，单位面积上的功率
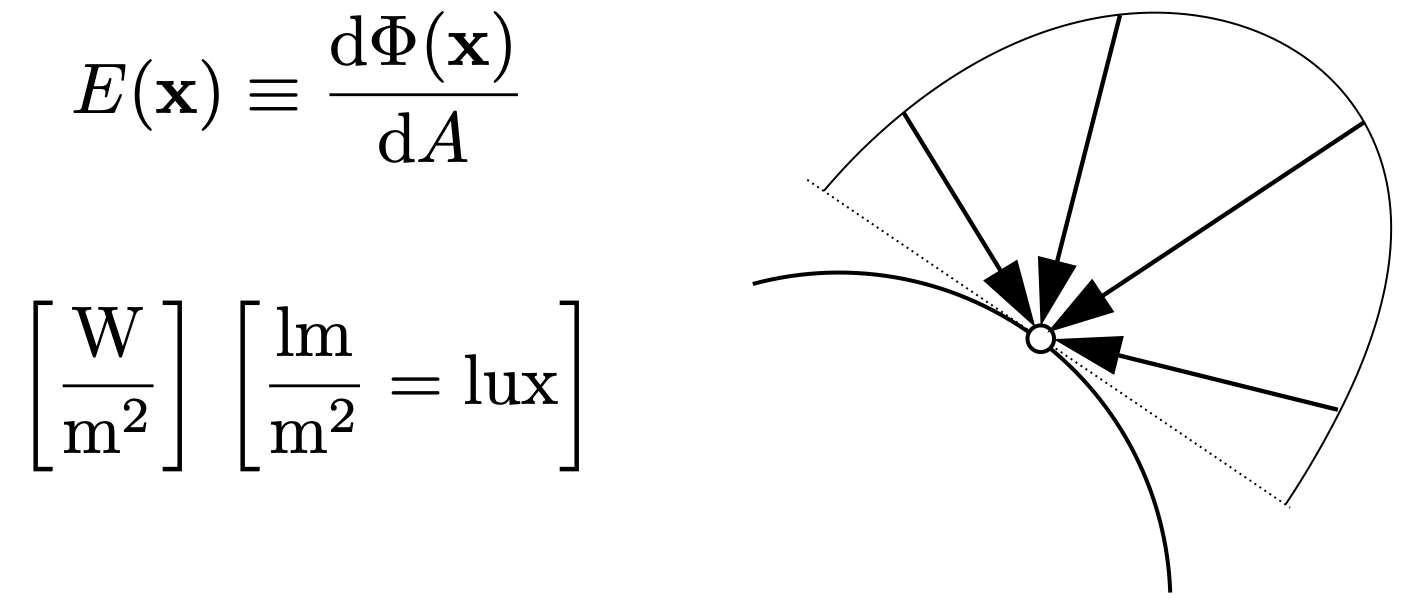
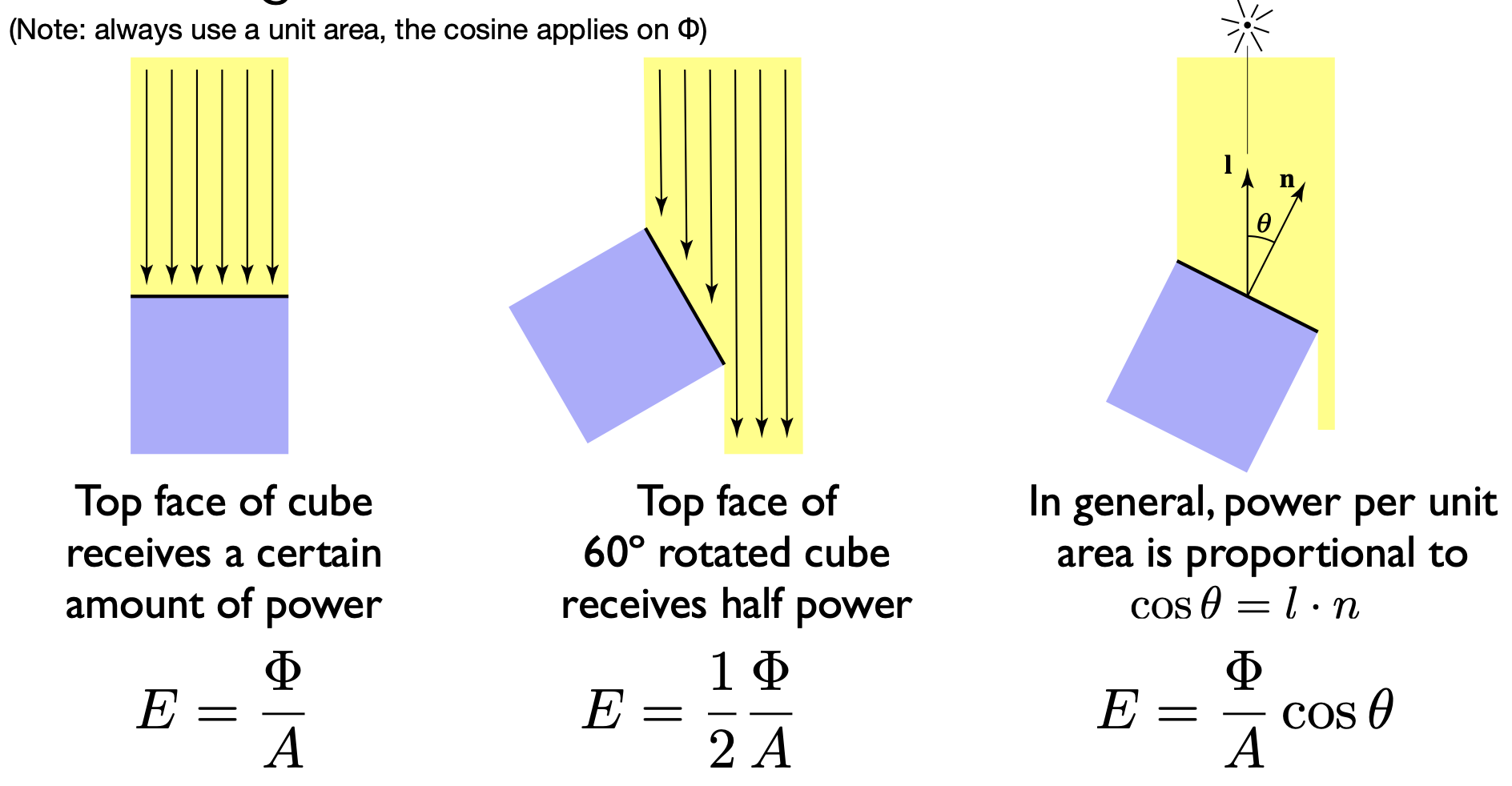
- 入射光需垂直于面，否则需进行投影

重新理解 Lambert’s Cosine Law

表面处的辐照度，与光方向和表面法线之间的夹角的余弦值成正比

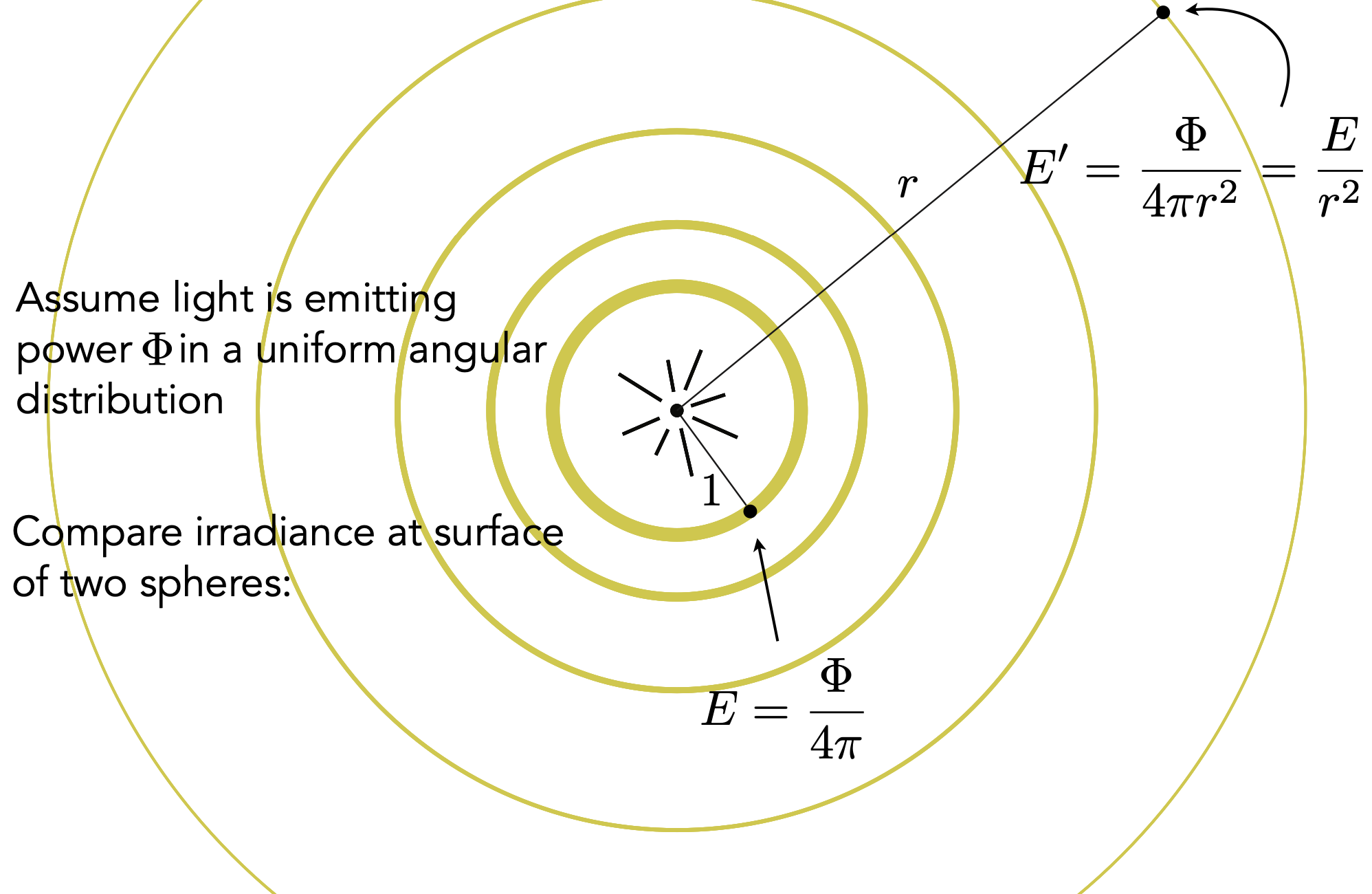
重新理解 Irradiance Falloff

在Blin-Phong模型中用到的光线强度随 r2 的衰减的正确理解：光线在传播过程中，irradiance衰减(面积增加)，intensity不变(立体角没变)

截屏2023-05-03 14.42.41

Radiance $L$

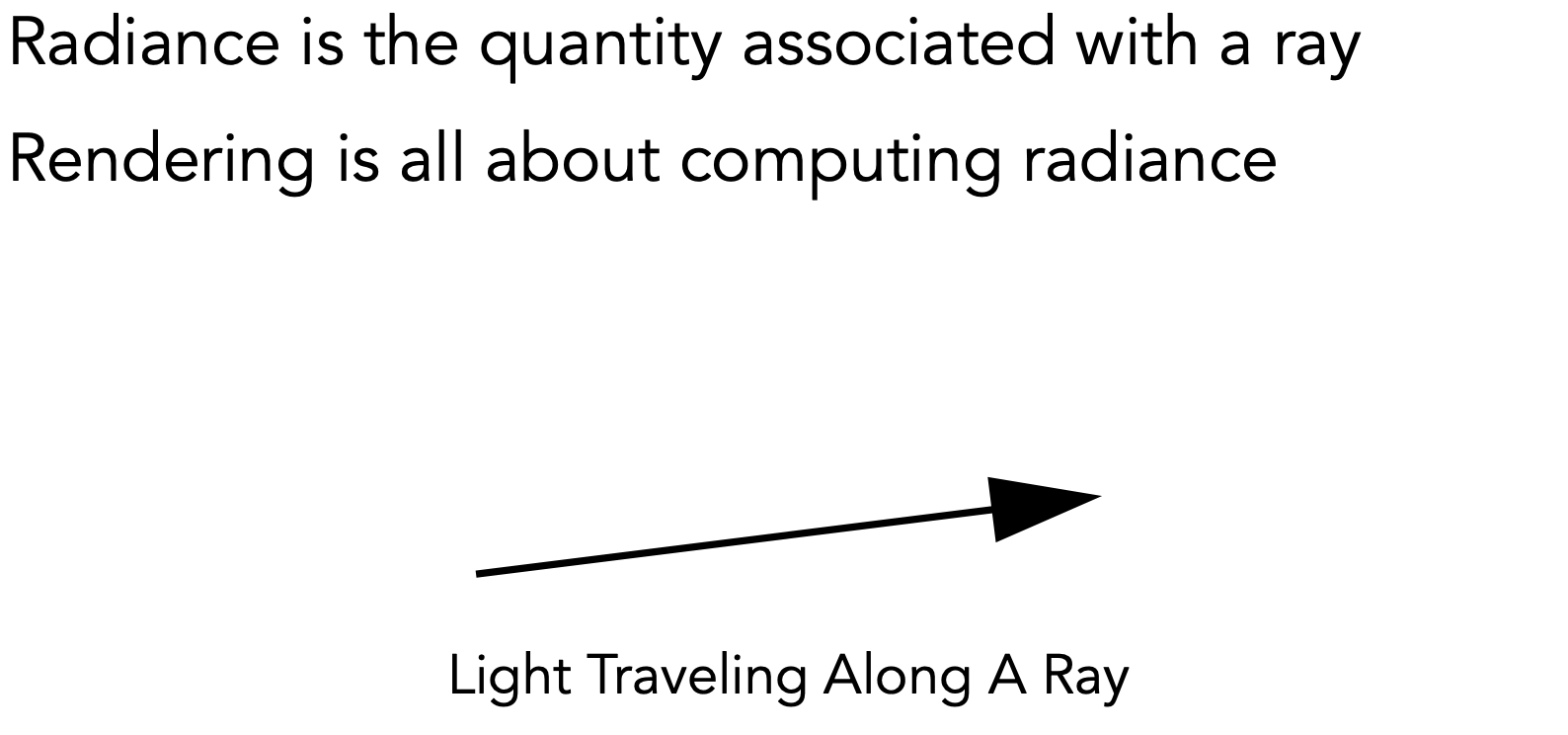
截屏2023-05-03 14.58.07

为了描述光线在传播过程中能量的度量
Radiance：power，在单位角per unit solid angle，单位投影面积上per projected unit area，上发射、反射、投射、接受的量

对比Irradiance、Intensity、Radiance

截屏2023-05-03 15.05.15

Incident Radiance 入射
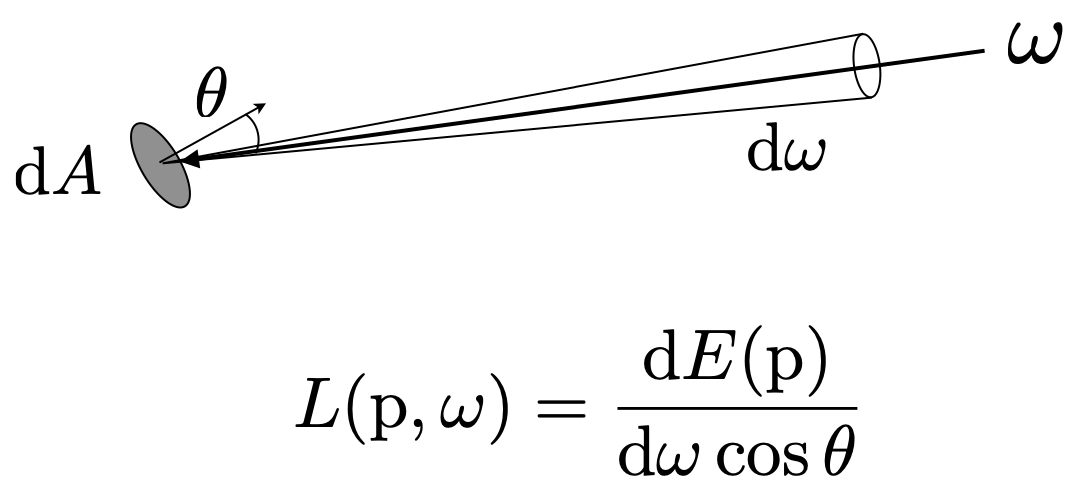
- Incident radiance is the irradiance per unit solid angle arriving at the surface
- 是沿着给定光线（表面点和入射方向）到达表面的光
Exiting Radiance
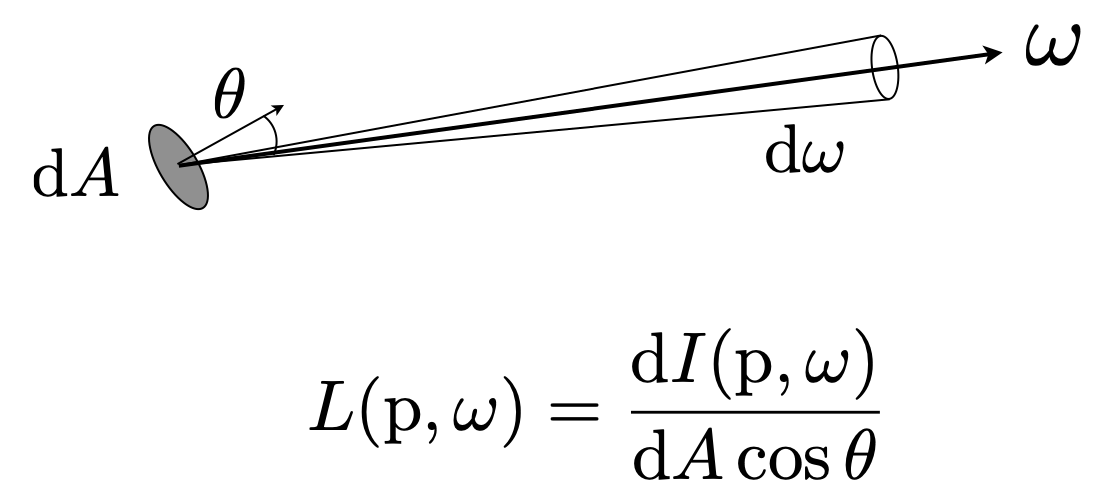
- Exiting surface radiance is the intensity per unit projected area leaving the surface.
- 对于区域光，它是沿给定光线（表面上的点和出口方向）发射的光
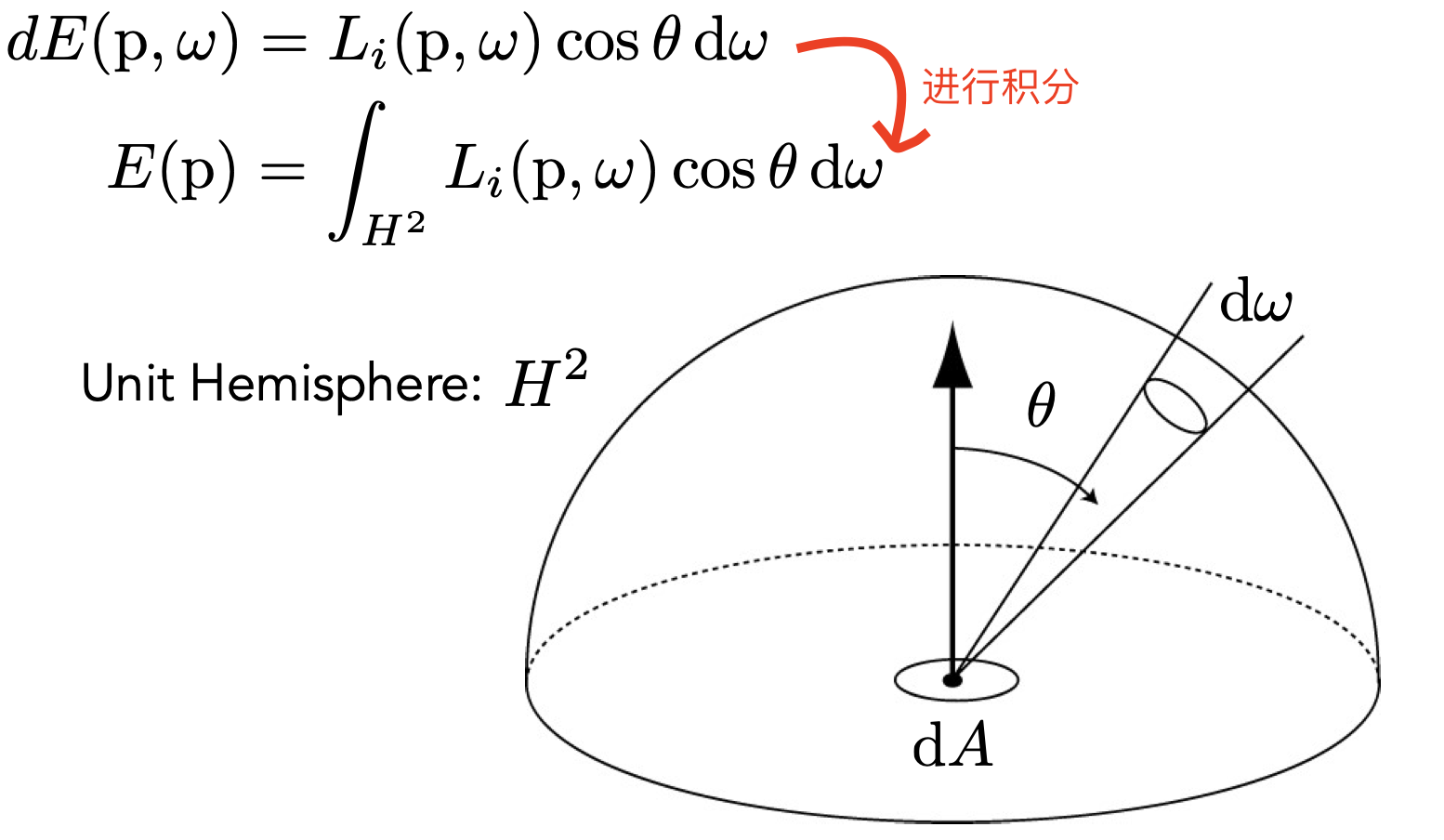
Irradiance vs. Radiance
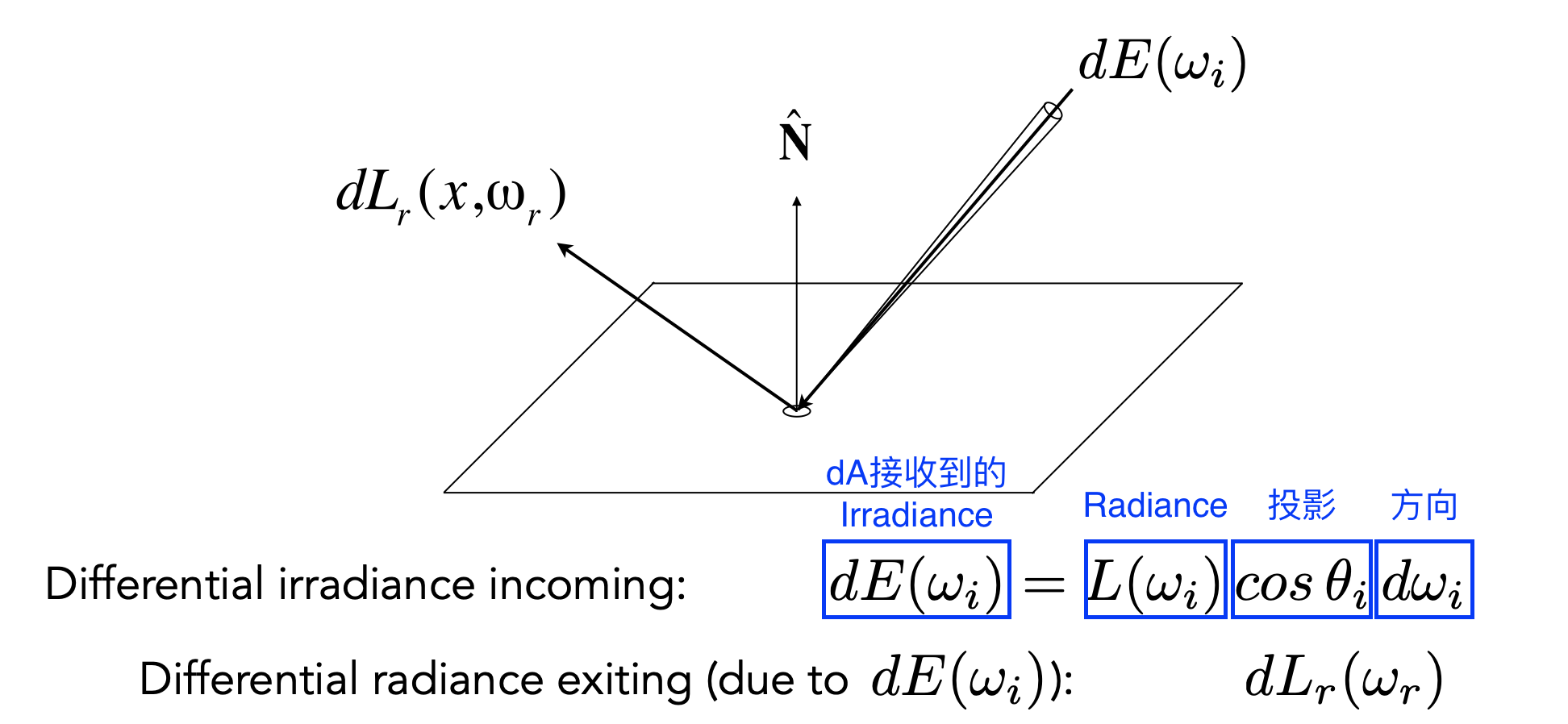
- Irradiance $E$ ：$dA$ 收到的所能量
- Radiance $L$ ：针对Irradiance作出特定方向立体角 $d\omega$ 的限制

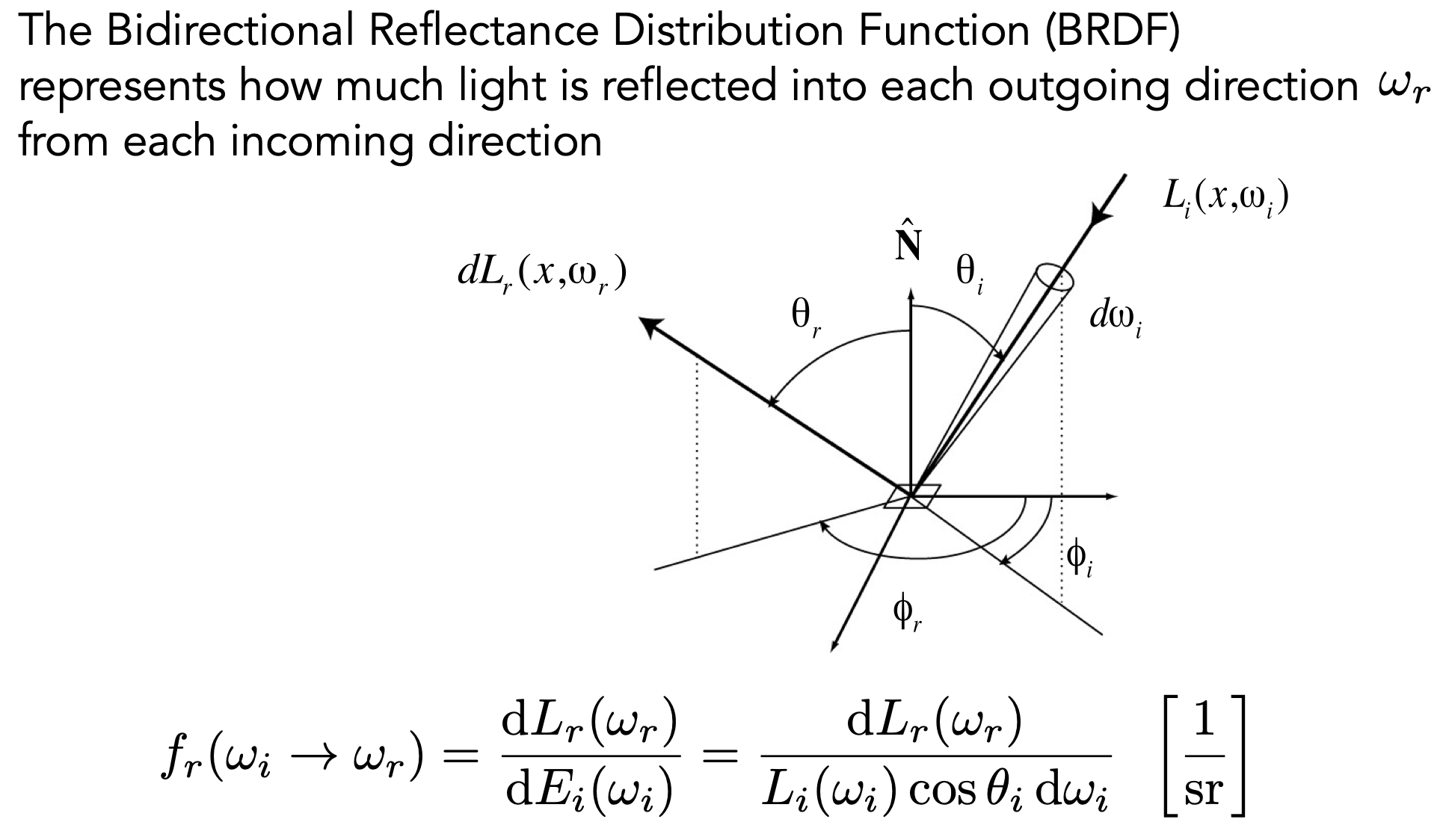
BRDF (Bidirectional Reflectance Distribution Function 双向反射分布函数)

定义一个函数描述不同表面的反射特性——从某个方向入射的光线，反射到另一个特定方向上的能量是多少

Reflection at a Point
- 来自direction $\omega _i$方向的Radiance变成了 $dA$ 吸收的power $E$ ；而后power $E$ 变成了向 direction $\omega$ 的辐射的Radiance
- BRDF
- 是针对一个方向，出射Radiance($dL_r(\omega_r)$)/入射Irradiance($dE(\omega _i)$)的比例。作用是将接收到的 $dE(\omega _i)$ 分配到不同的立体角
- 用于定义不同材质

Reflection Equation 反射方程

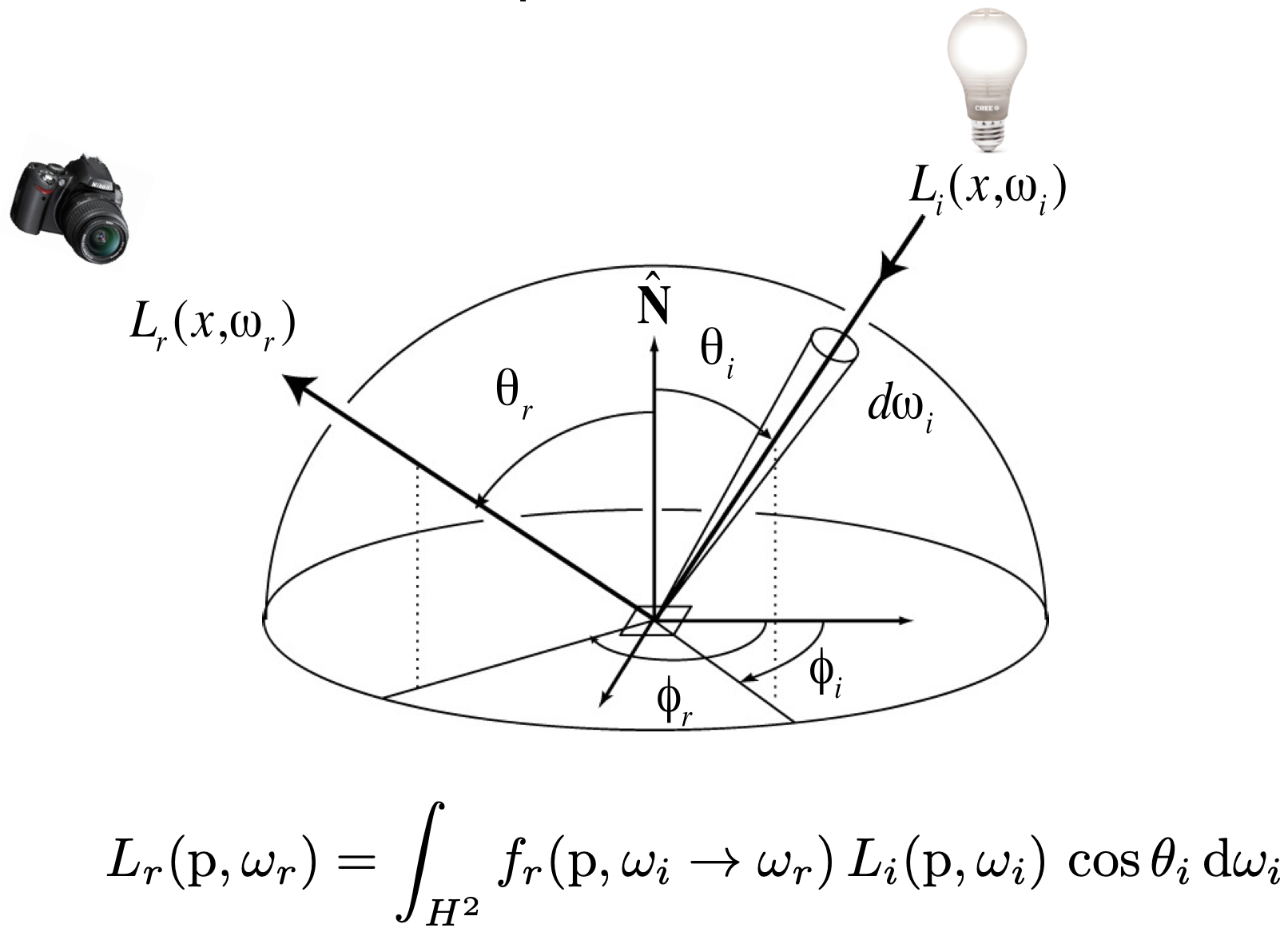
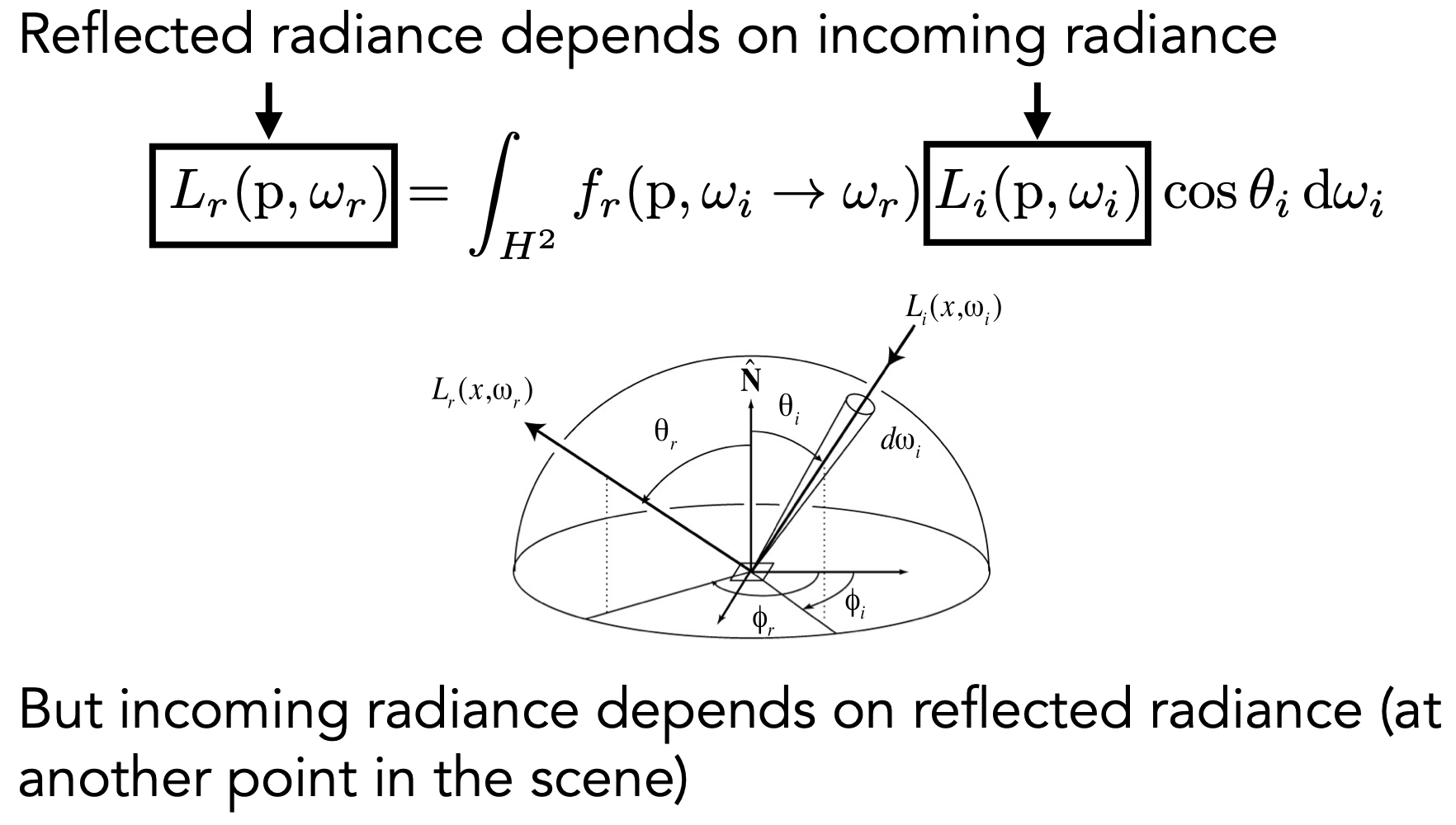
考虑任何一个方向的入射光，对观察点反射光的贡献，叠加所有方向光的贡献，得到该点最终渲染效果
对每个方向的入射irradiance $dE(\omega _i)$ （也就是 $L_i(p,\omega_i)cos\theta_i d\omega_i$ ）都乘BRDF，而后对方向积分，得到出射Radiance $L_r(p,\omega_r)$ ，进而得出最终的观察结果
Challenge: Recursive Equation 递归方程
- 入射的Irradiance不只来自光源，也来自其他物体的反射（递归）

Rendering Equation 渲染方程

Intro

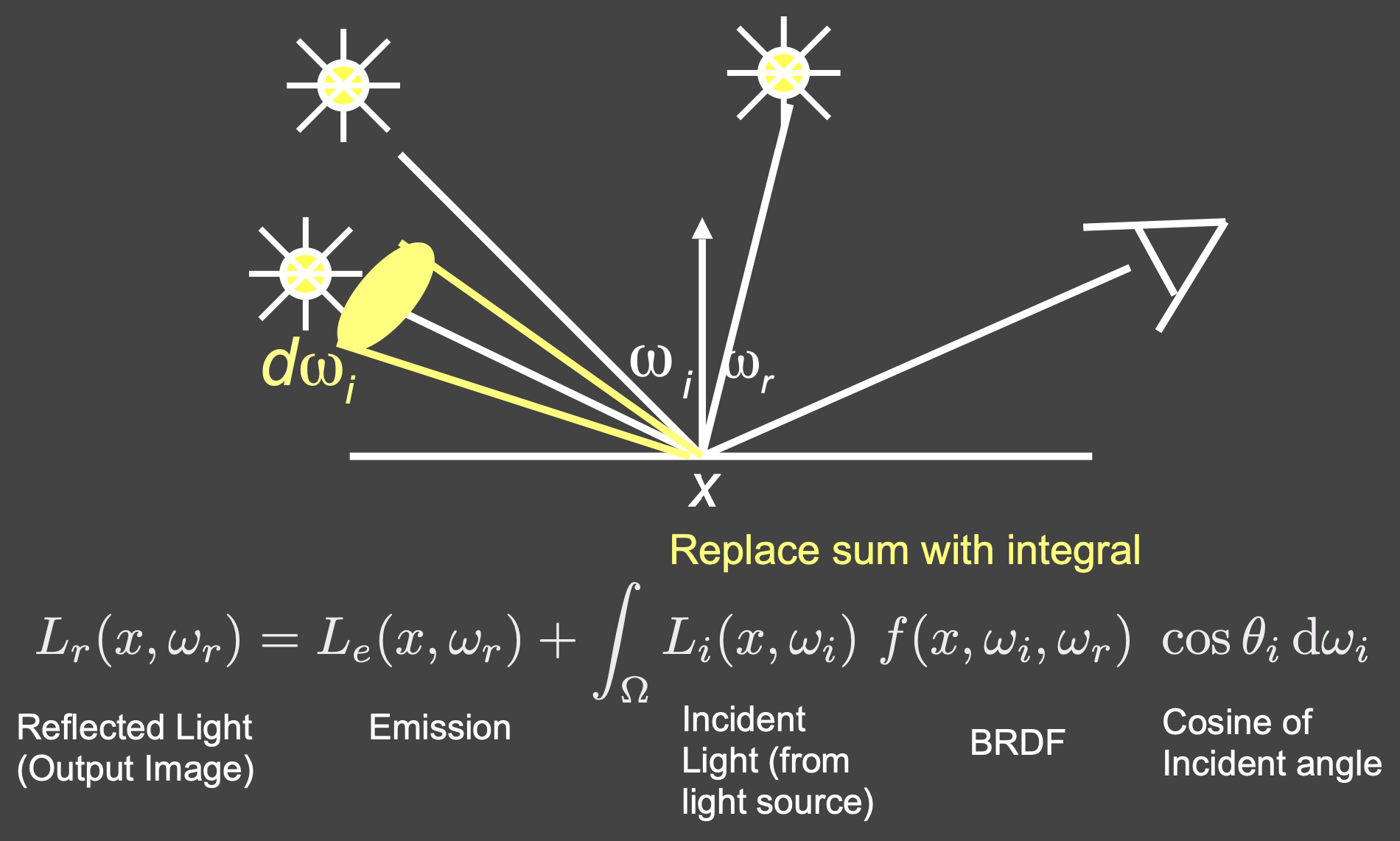
上述Reflection Equation忽略了自发光，Rendering Equation添加了自发光项，可用于所有类型的光线传播

截屏2023-05-03 18.29.34

理解渲染方程

一个方向的光$\rightarrow$多个方向的光：累加
引入面光源：积分面光源所占的立体角

渲染方程的递归简化求解

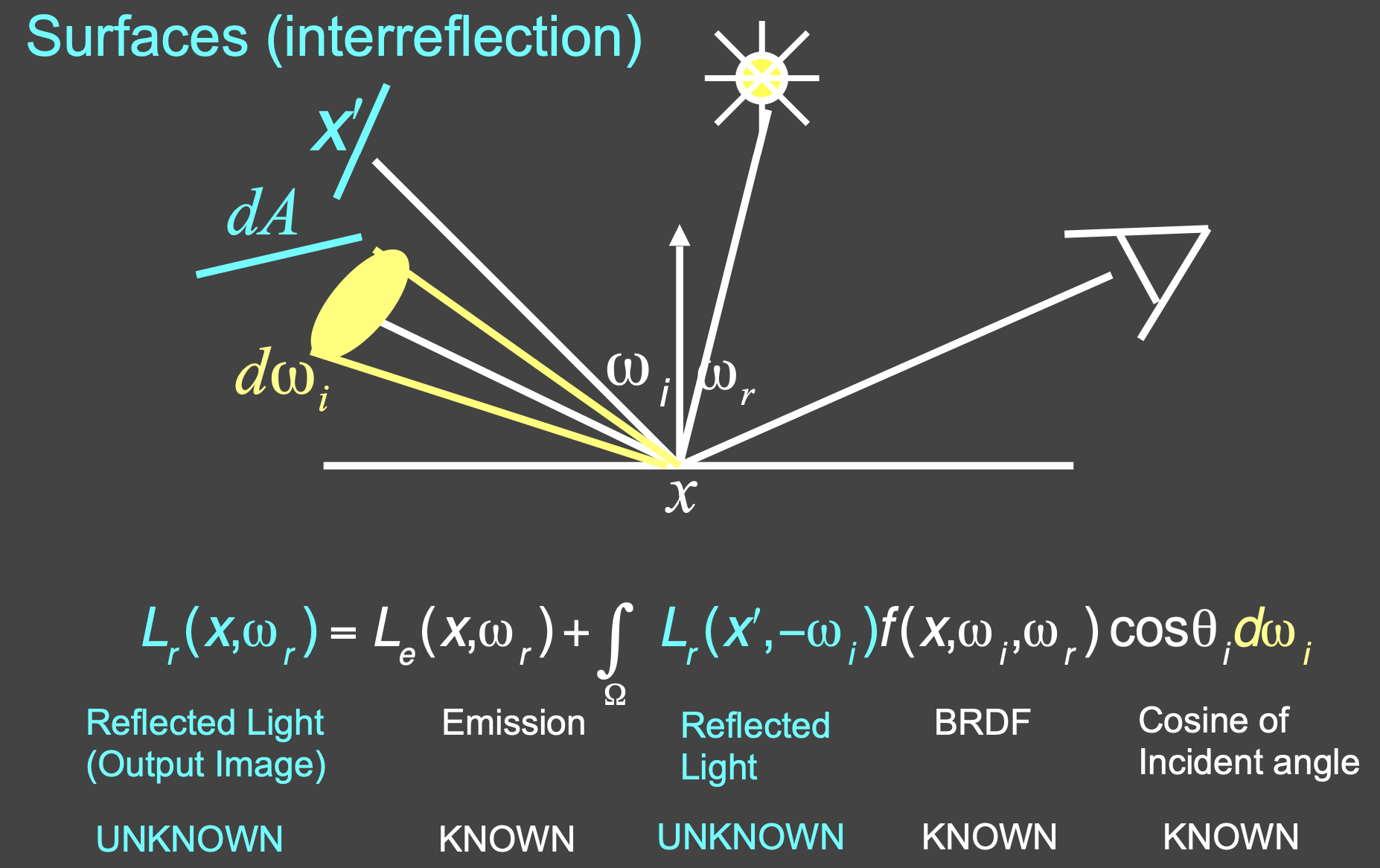
- 未知量：入射&出射Radiance
渲染方程的简化
- 用 $l$ 表示不同位置辐射的Radiance，$u \& v$ 表示不同位置，简化为线性积分
- 线性积分进一步简化
  - 简化为了求解渲染方程，即求解 $L$
  - $K$ 为反射算子，是矩阵形式
求解渲染方程
- 其中 $I$ 为identity单位矩阵
- 通过一些类似泰勒展开的操作进行近似 $(1+x)^\alpha = 1+\alpha x + \frac{\alpha(\alpha -1)}{2!}x^2+\frac{\alpha(\alpha -1)(\alpha -2)}{3!}x^3+…$ （矩阵居然也可以！？？！）
- 得到了！
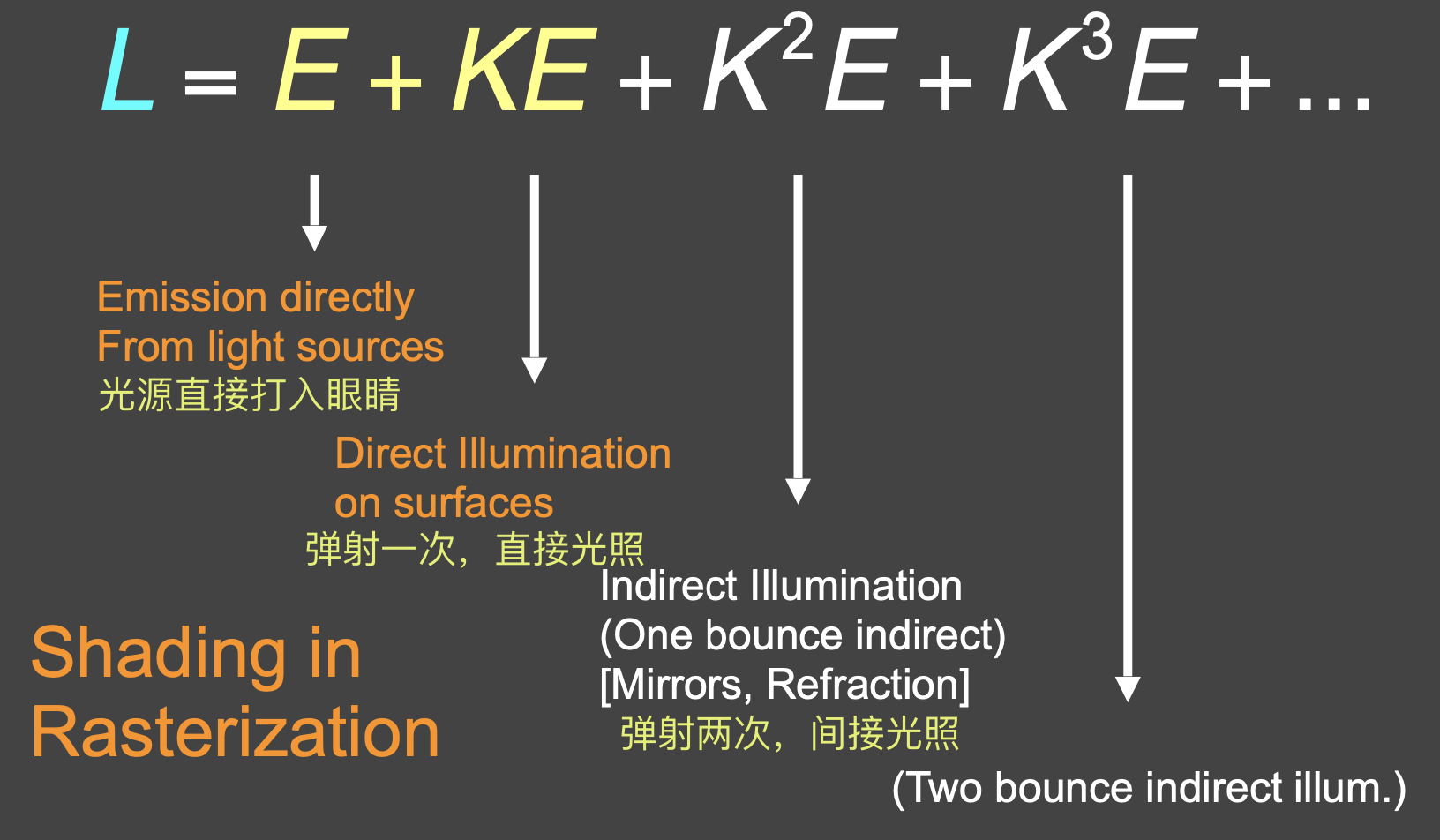
  - 所有光线弹射（直接+所有间接）相加，得到全局光照（Global illumination，GI）
  - 注：光栅化一般只能做到直接光照；间接光照光追容易做
对比
- 关于Two - bounce上方的灯为什么是黑色：从摄影机出发的光线，经过两次弹射还无法从灯中射出（两次弹射进入一个玻璃层，再经过两次弹射方可从另一玻璃层射出）
- 假设可以做无限次光线弹射：亮度收敛到最大值，不会无限增大（泰勒无限展开，无限逼近）
路径追踪是解渲染方程的一种方式

概率论回顾 Probability Review

苍天啊！！！！！！！！

Random Variables 随机变量
Probabilities
- $n$ 中情况：$x_i$
- with probability：$p_i$
- 满足
  - $p_i\geq 0$
  - $\sum_{i=1}^n p_i = 1$
Expected Value of a Random Variable 期望
Continuous Case 连续情况下描述变量和分布
- 概率密度函数 Probability Distribution Function (PDF)
Function of a Random Variable 随机变量的函数

P16 Ray Tracing4 (Monte Carlo Integration & Path Tracing)

Monte Carlo Integration 蒙特卡洛积分

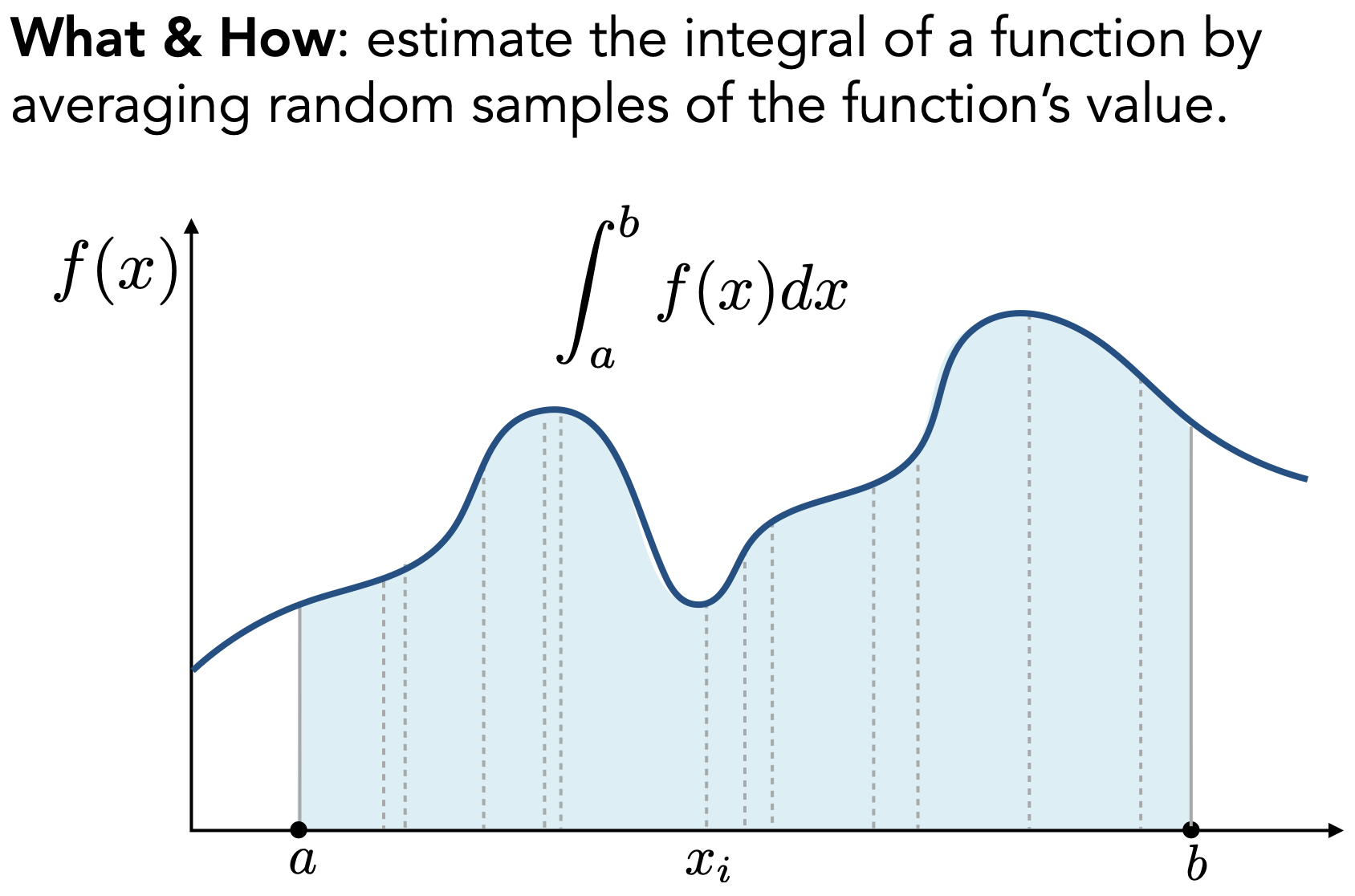
如何使用：在积分域内，对样本不断随机采样，做平均，近似函数积分数值
特例情况：均与采样（a~b间均匀采样，则采样PDF为常函数）
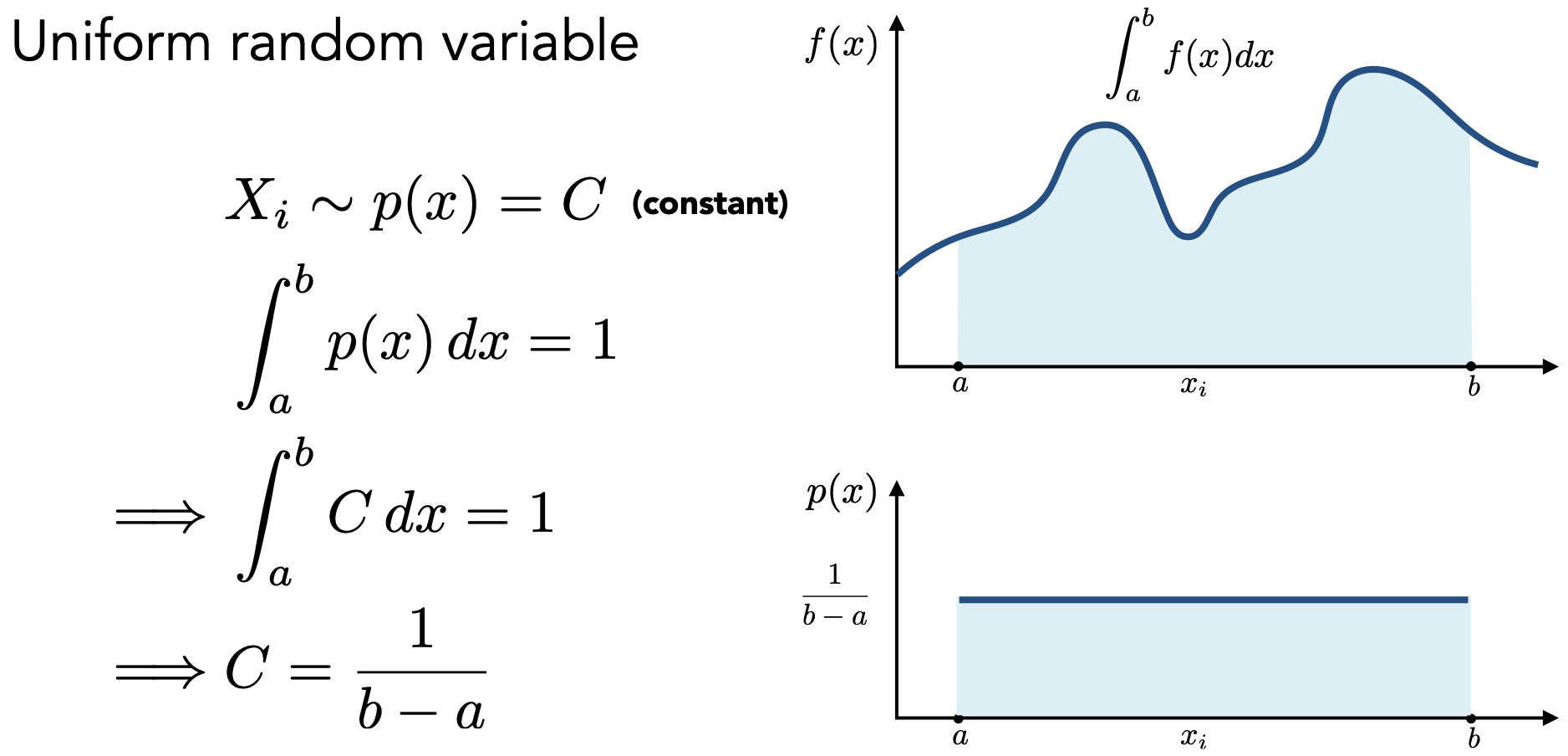
- 上图已求解出了 $p(x)$ ，带入 $F_N$
通用情况：非均匀采样（PDF不为常函数）
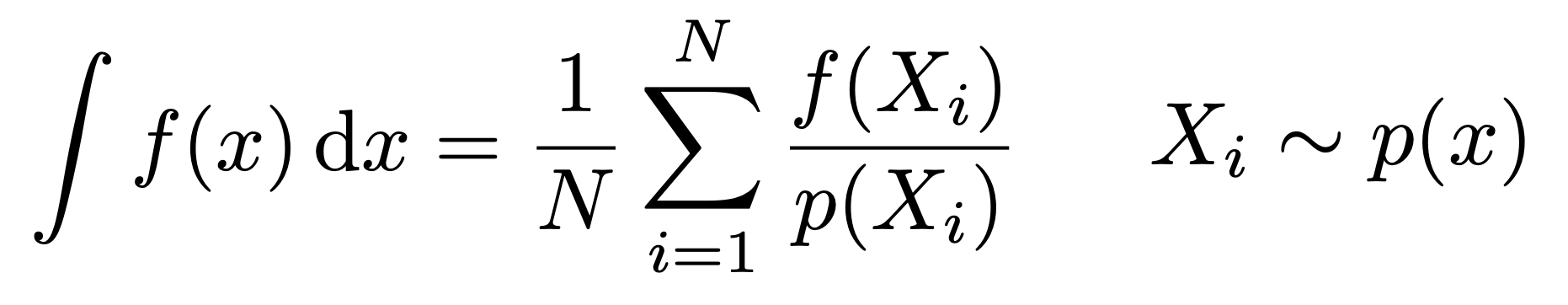
- 注意
  - 样本越多，近似越准确
  - 在 $x$ 积分，则对应在 $x$ 采样
  - 除以 $p(X_i)$ 相当于为非均匀的采样加权（上述均匀采样权重相同，因此 $p(X_i)$ 就是常数）

Path Tracing 路径追踪

对比 Whitted-style ray tracing

回顾 Whitted-style ray tracing
- 始终执行镜面反射/折射
- 在漫反射表面上停止反射
BUT!!! Whitted-style ray tracing is not totally based on physics, which needs to be improved!!!
Problems of Whitted-style ray tracing
- 只可以镜面反射or折射——无法表现glossy reflection
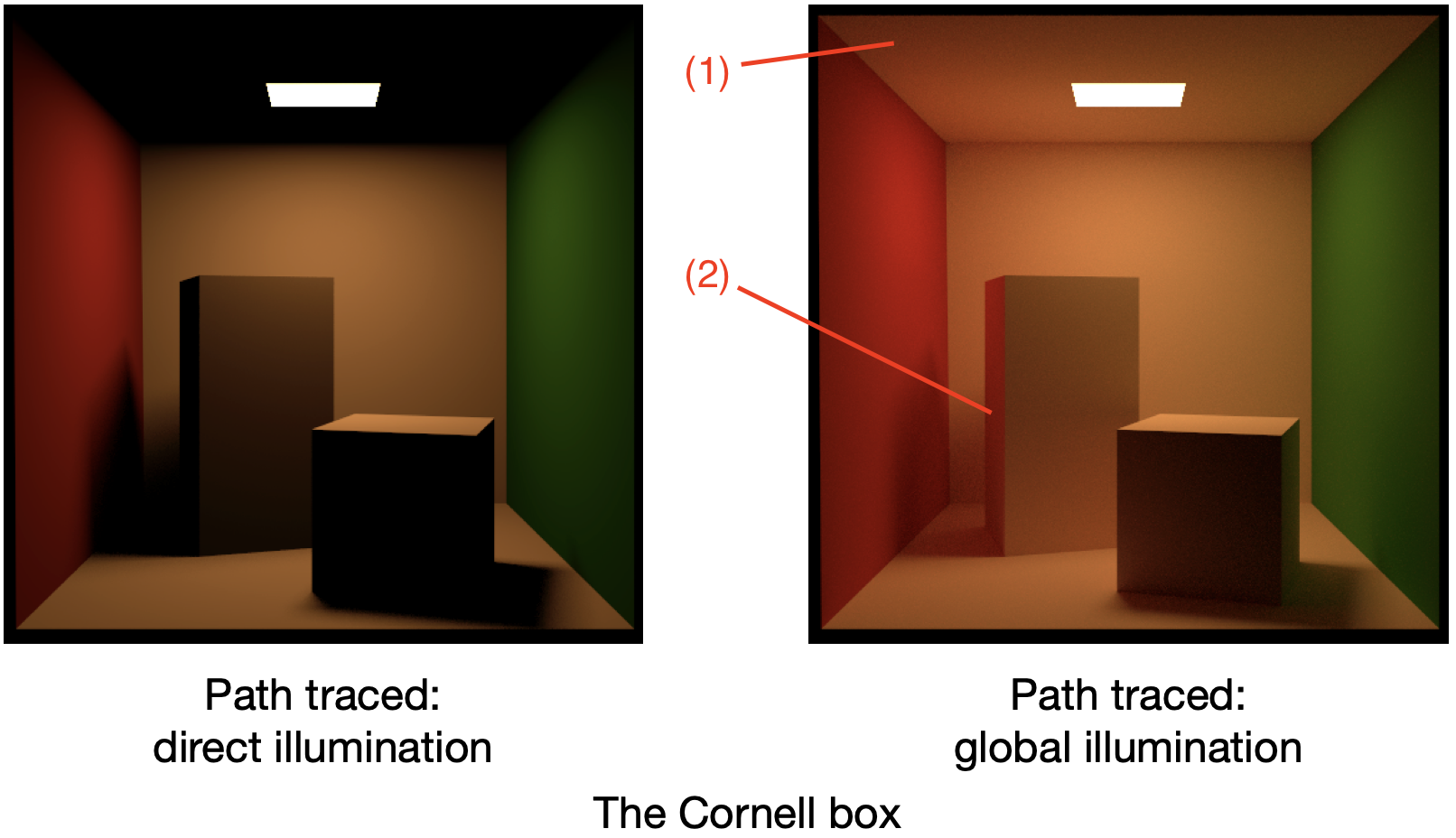
- 遇到漫反射物体，光线停止传播——忽略了漫反射物体间的光线传播(1)；无法表现Color Bleeding(2)
But!!! The rendering equation is correct!!!
- 需要求出光照，则需求解渲染方程
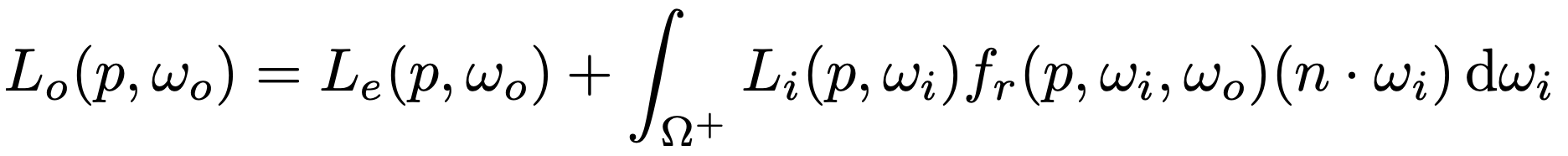
- 需要解决
  - STEP1: 半球域内的定积分——蒙特卡洛积分
  - STEP2: 递归

A Simple Monte Carlo Solution(to solve the rendering equation)

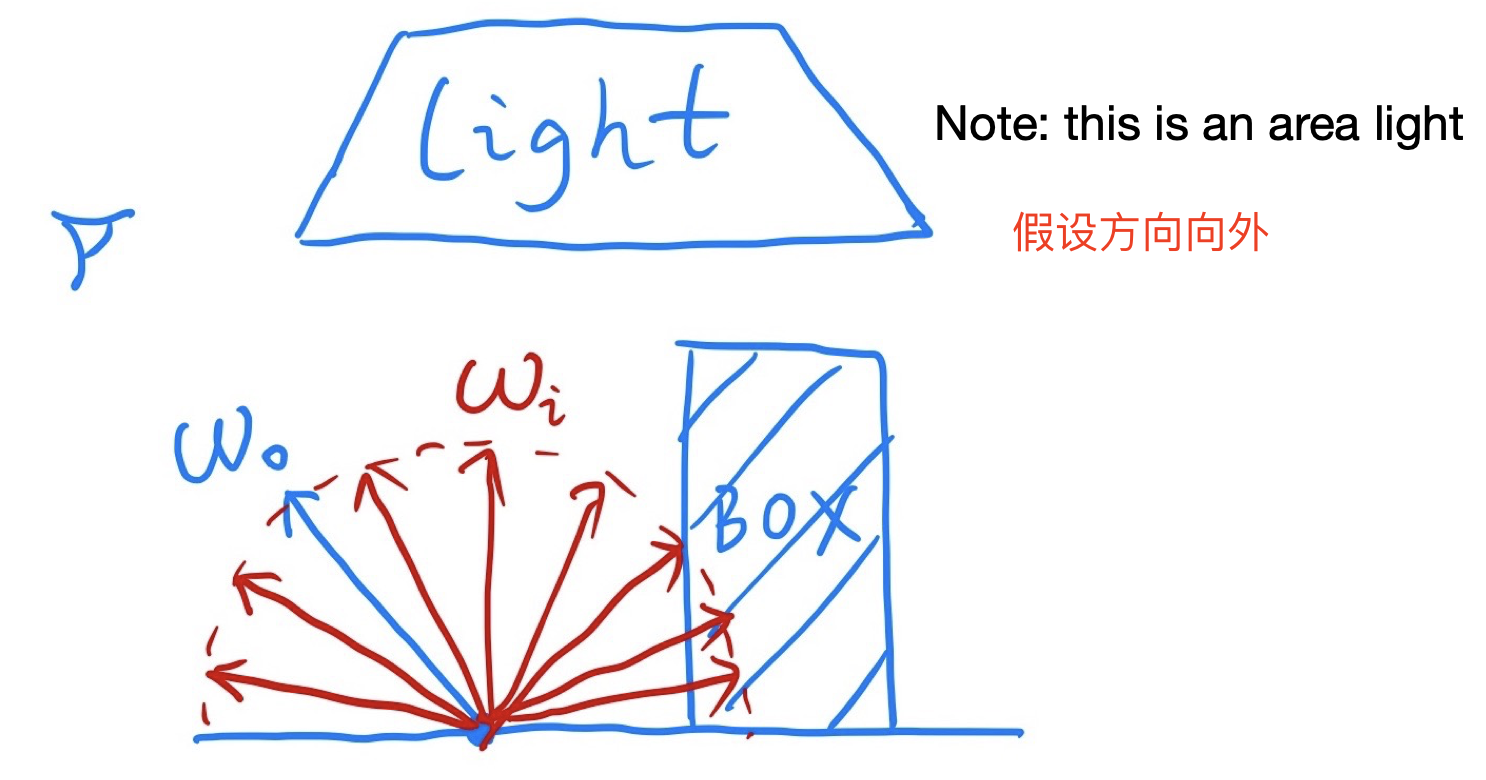
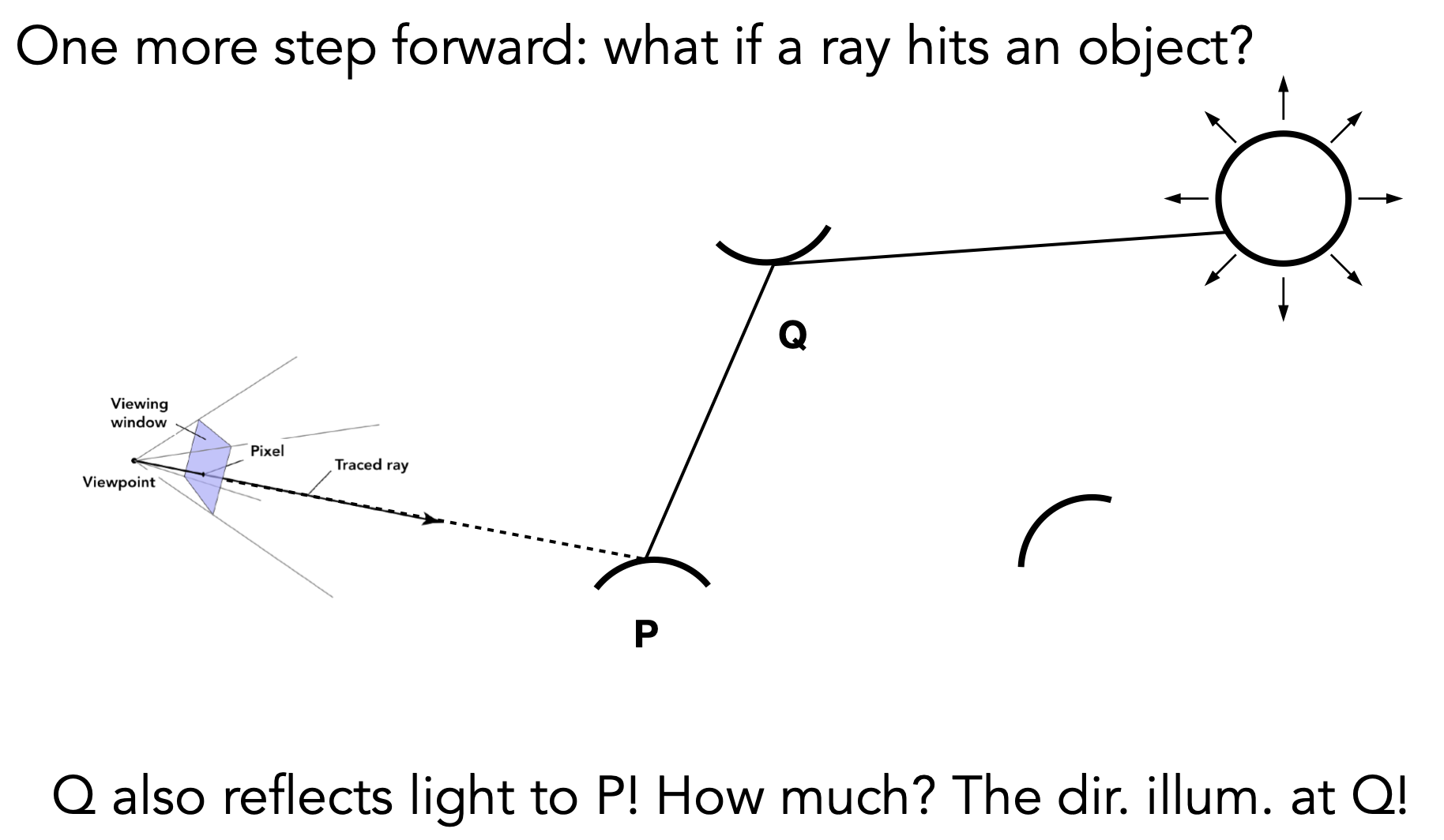
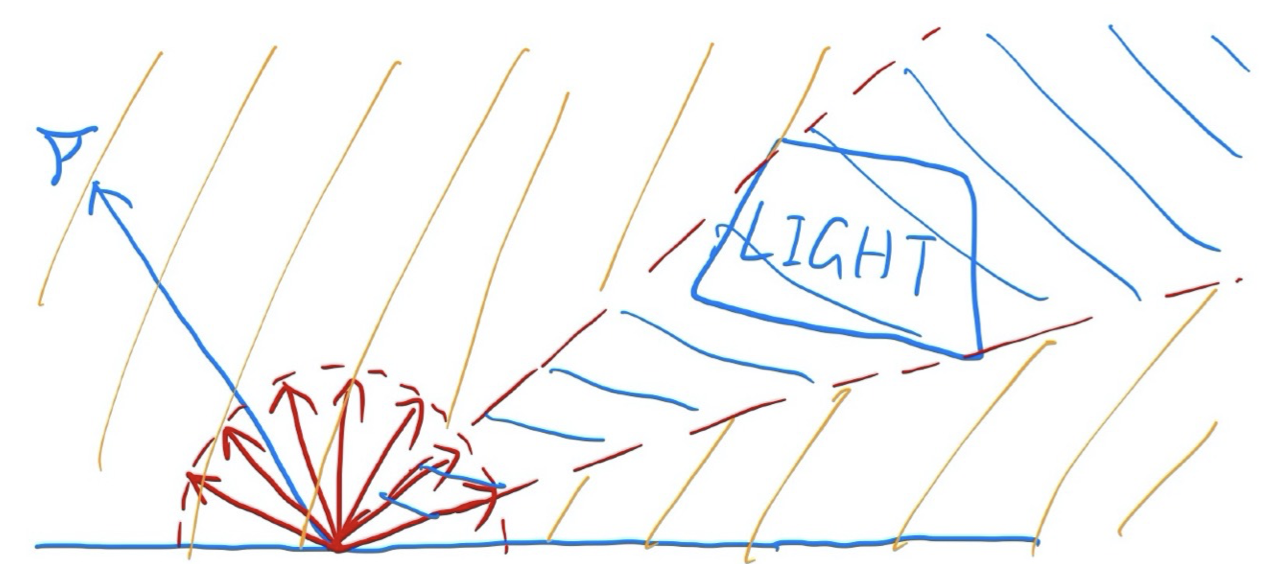
假设一种简单情况，即只渲染如图所示一个point的直接光照
直接光照条件下，$L_i$ 只可能来自光源
利用蒙特卡洛积分（暂且忽略渲染方程的自发光项）
- $f(X_k)$ ：积分内函数整体
- PDF：假设对半球进行平均的采样，则 $p(X_k)$ 为常数 $1/2\pi$
将渲染方程写成蒙特卡洛积分后形式
- 意义：得出一种正确的直接光照算法，可以算出着色点point出射的Radiance
只考虑直接光照的，path tracing的，$shade(p,wo)$ 伪代码

Global Illumination (引入递归)

截屏2023-05-04 22.27.06

$shade(p,wo)$ 伪代码

Problems & Solving Problems(Ray Generation & Russian Roulette)

上述解决方法的问题
- Problem1: Explosion of #rays as #bounces go up （N为反射打出的光线数）
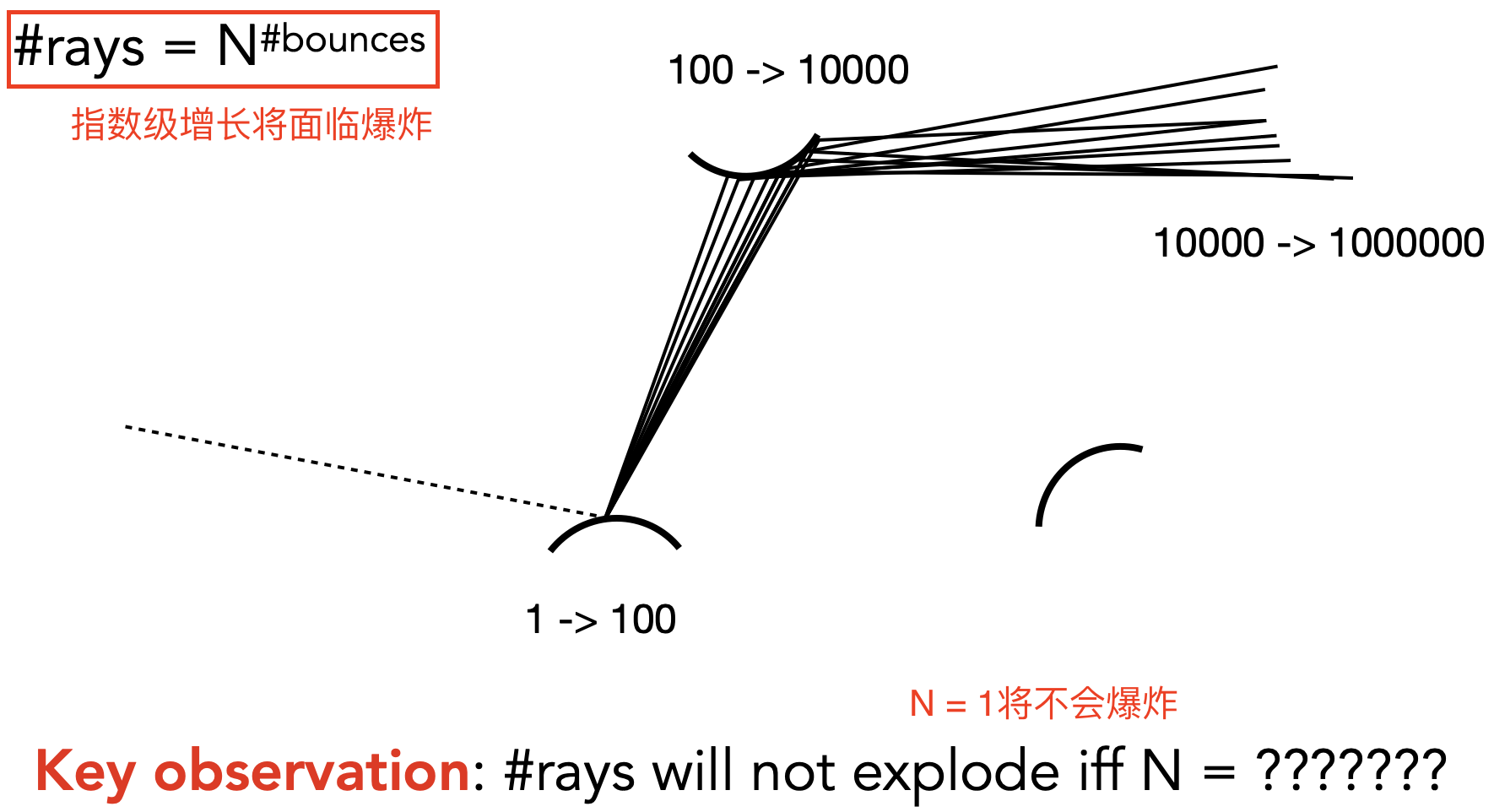
  - 解决explosion的方法：N = 1（Path Tracing就是N=1时做蒙特卡洛积分）
  - $shade(p,wo)$ 伪代码
  - N = 1会引起Noise，不过可以对一个像素trace more paths并求平均进行解决
    - 引入Ray Generation
- Problem2: 递归无法停止
  - 真实世界光线无限弹射
  - 减少弹射次数 == 能量损失，因此不能强制终止
  - 解决方法：引入Russian Roulette (RR)俄罗斯轮盘赌——一定的概率停止继续追踪
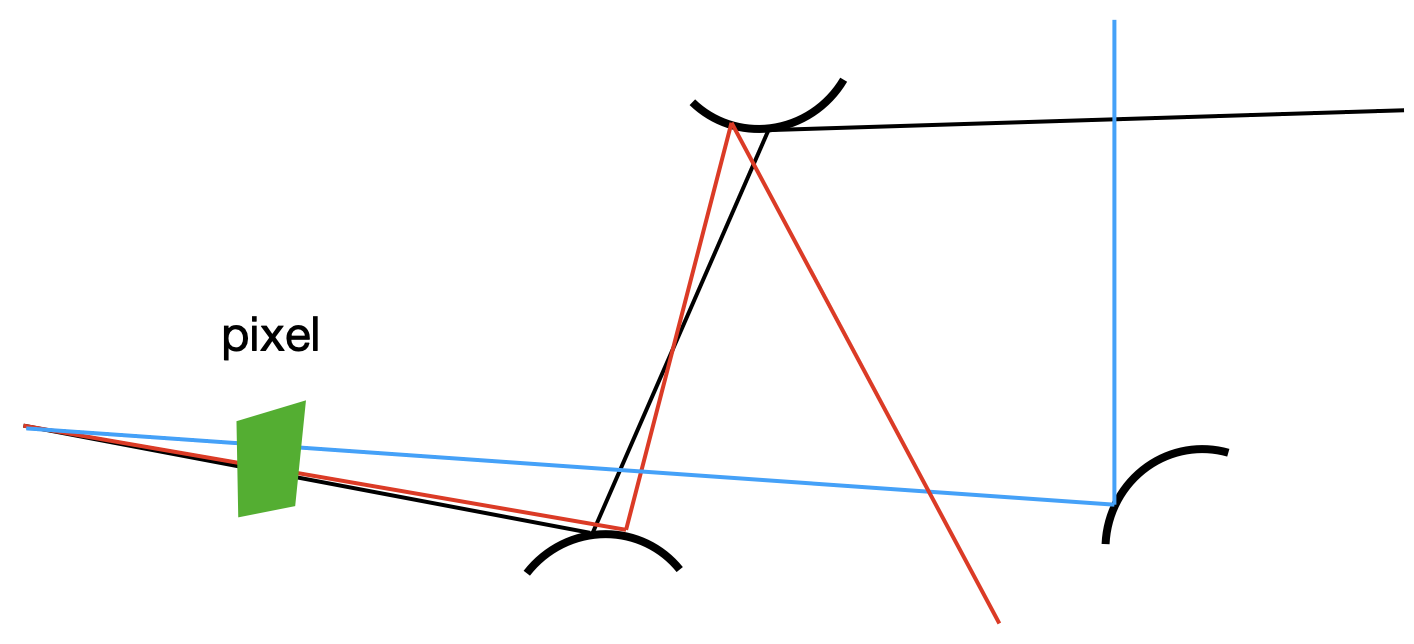
Ray Generation: 相机如何产生光线路径
Russian Roulette (RR)俄罗斯轮盘赌
- - 通过计算期望 $E$，最后虽然有Noise，但结果 $L_o$ 一定正确
- $shade(p,wo)$ 伪代码

Path Tracing 优化

SPP (samples per pixel) 
- 目的：提升Low SPP下效率
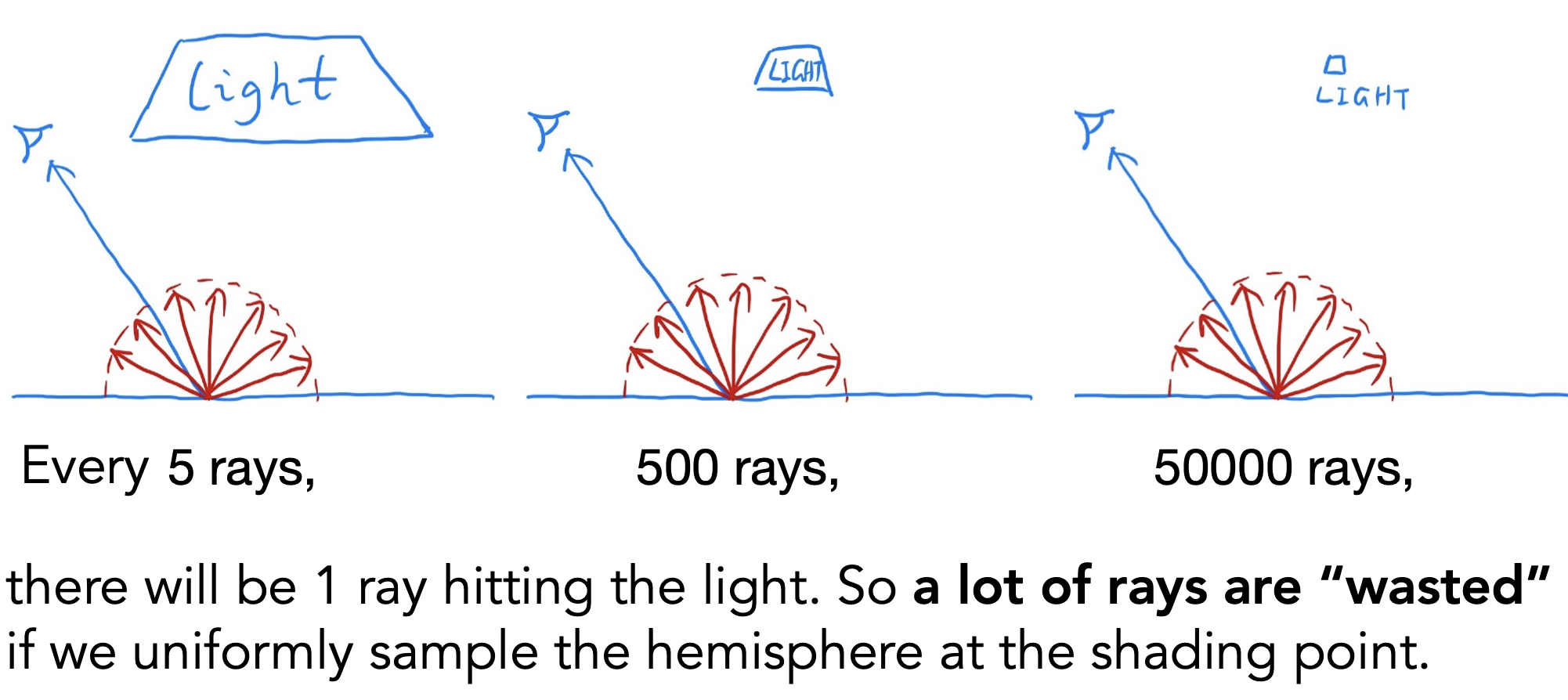
效率低的原因：光源小、PDF为常数（均匀采样）时，假设每50000根光线才有1根达到光源，许多光线被浪费
优化思路：Sampling the light（针对伪代码中“hit the light”的判断）
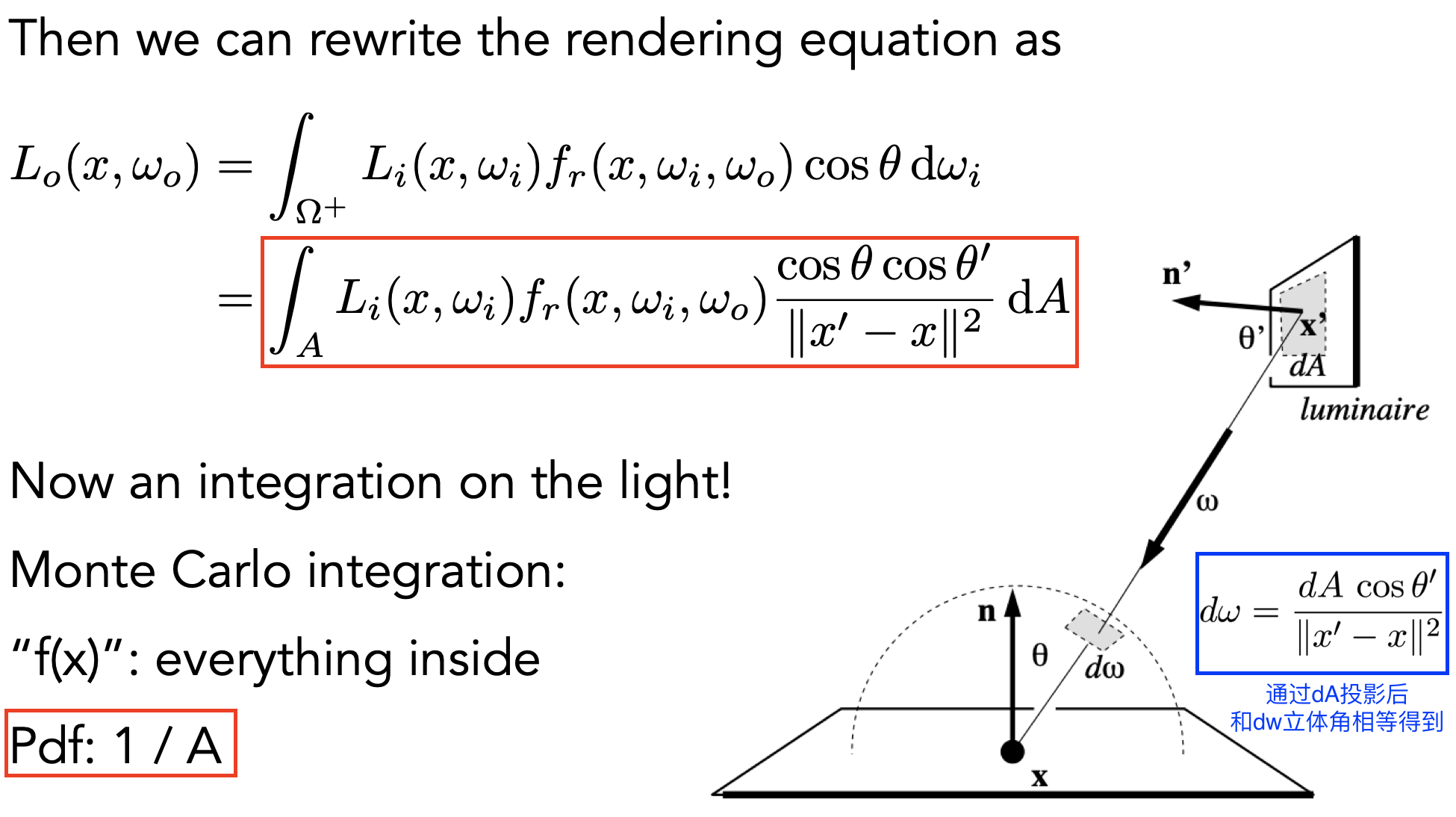
- 采样的光路全分布在光源表面；对渲染方程的积分换元（改变积分域），从 $d\omega$ 换成光源面积 $dA$，PDF = 1/A
- 注⚠️：该方法不好算点光源，建议将点光源换成小面光
- 找到 $d\omega$ 和 $dA$ 的关系，并重写渲染方程

进一步改进 $shade(p, wo)$ 伪代码

将光源分成直接光照 & 间接光照，分开计算（此处未考虑遮挡）
- light source (direct直接光照, no need to have RR)
- other reflectors (indirect间接光照, RR)

shade(p, wo)
    // Contribution from the light source. 直接光照
    Uniformly sample the light at x’ (pdf_light = 1 / A)
    L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light //优化重写后的渲染方程

    // Contribution from other reflectors. 间接光照
    L_indir = 0.0
    Test Russian Roulette with probability P_RR // 引入俄罗斯轮盘赌
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi) 
      Trace a ray r(p, wi)
    If ray r hit a non-emitting object at q // 判断q需不为光源，才可以算进L_indir
            L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR 
      Return L_dir + L_indir