Games101-P21-22 Animation

Posted on Edited on In Word count in article: 1.8k

  • P21 Preview

    • Keyframe animation
    • Physical animation
    • Kinematics
    • Rigging

  • P22 Preview

    • Single particle simulation

      • Explicit Euler method

      • Instability and improvements

    • Rigid body simulation

    • Fluid simulation

P21 Animation

  • 帧率按需求设定；VR至少90fps

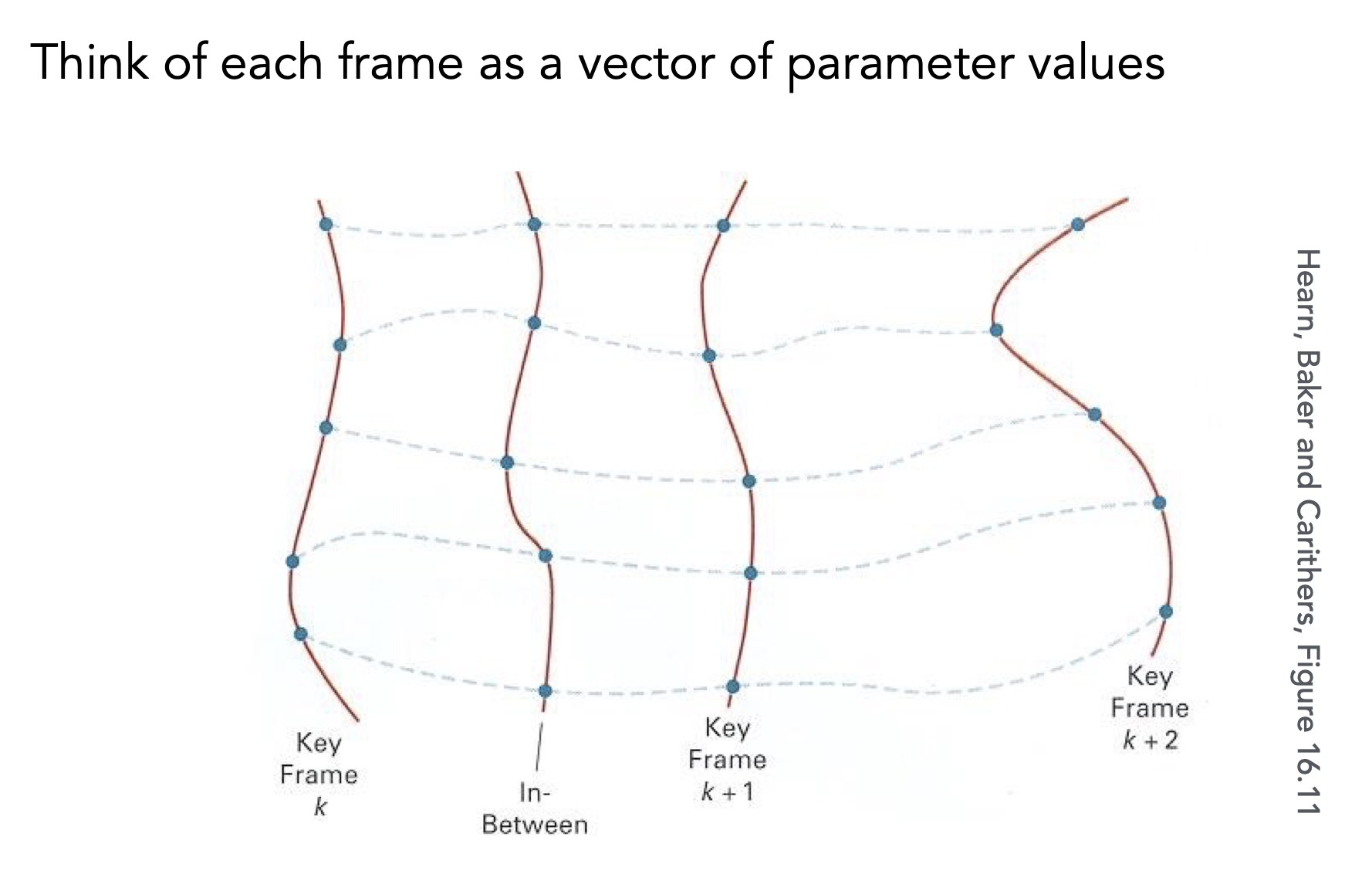
Keyframe

  • 给定一系列不同的帧，中间的帧通过插值（linear/non-linear）得到
    • 截屏2023-06-23 14.19.17

Physical Simulation

  • 牛顿定律 $F = ma$

Physically Based Animation

截屏2023-06-23 14.35.59

质点弹簧系统 Mass Spring System

  • Examples
    • hair
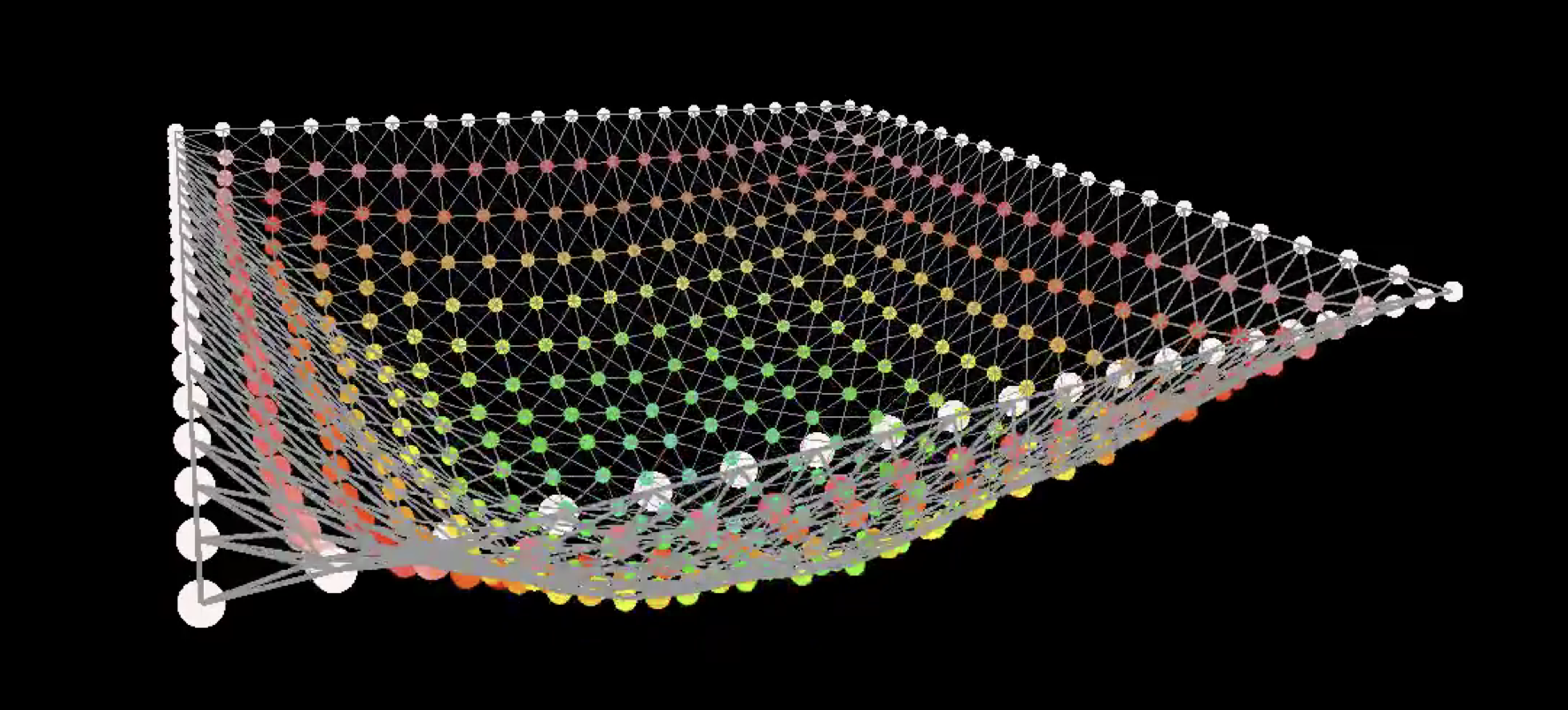
    • cloth截屏2023-06-23 14.41.18
模型建立
  • 模型基础：相互连接的质点和弹簧，考虑弹力和摩擦
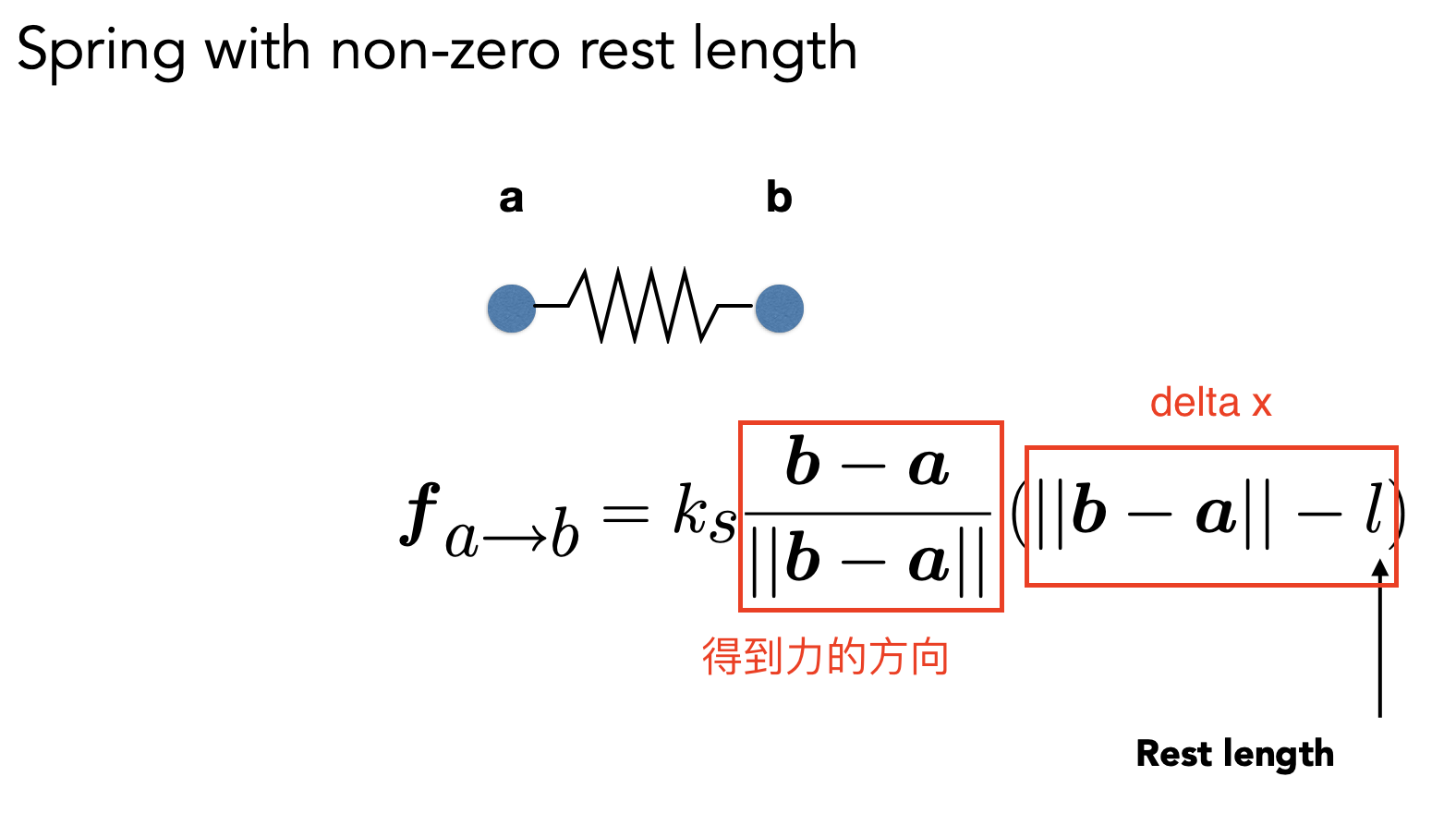
  • 胡克定律截屏2023-06-23 14.46.16
    • 问题：没有能量损耗，无限振动
  • 添加能量损失
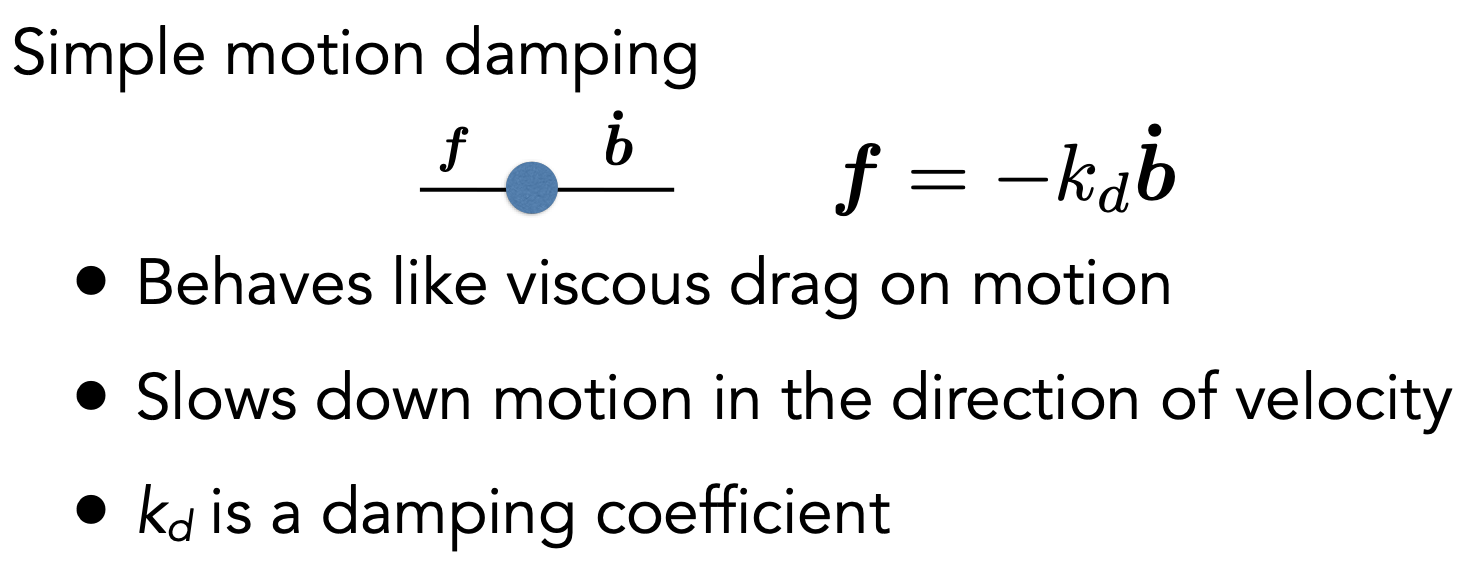
    • 截屏2023-06-23 14.51.03
    • 问题：该方法所添加的摩擦力只适用于外部力，对于弹簧内部相互作用力造成的损耗无法模拟
  • 添加内部相互作用力的能量损耗
    • 截屏2023-06-23 14.54.48
    • 摩擦力延ab方向（投影
    • 圆周运动，$f_b = 0$
弹簧的结构

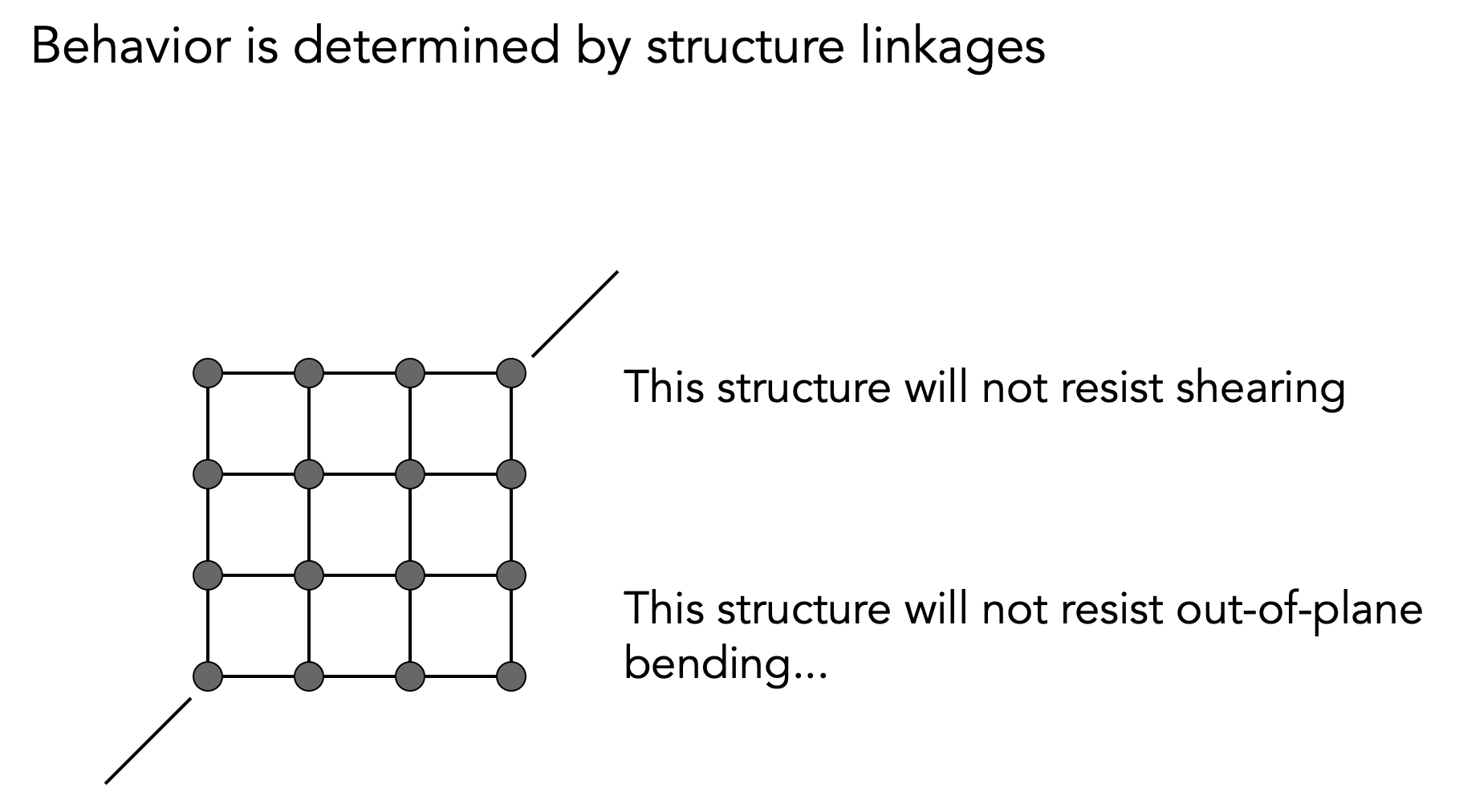
截屏2023-06-23 15.04.22

  • 上图结构无法模拟 & 如何解决
    • 对角线拉扯：出现切变的形变
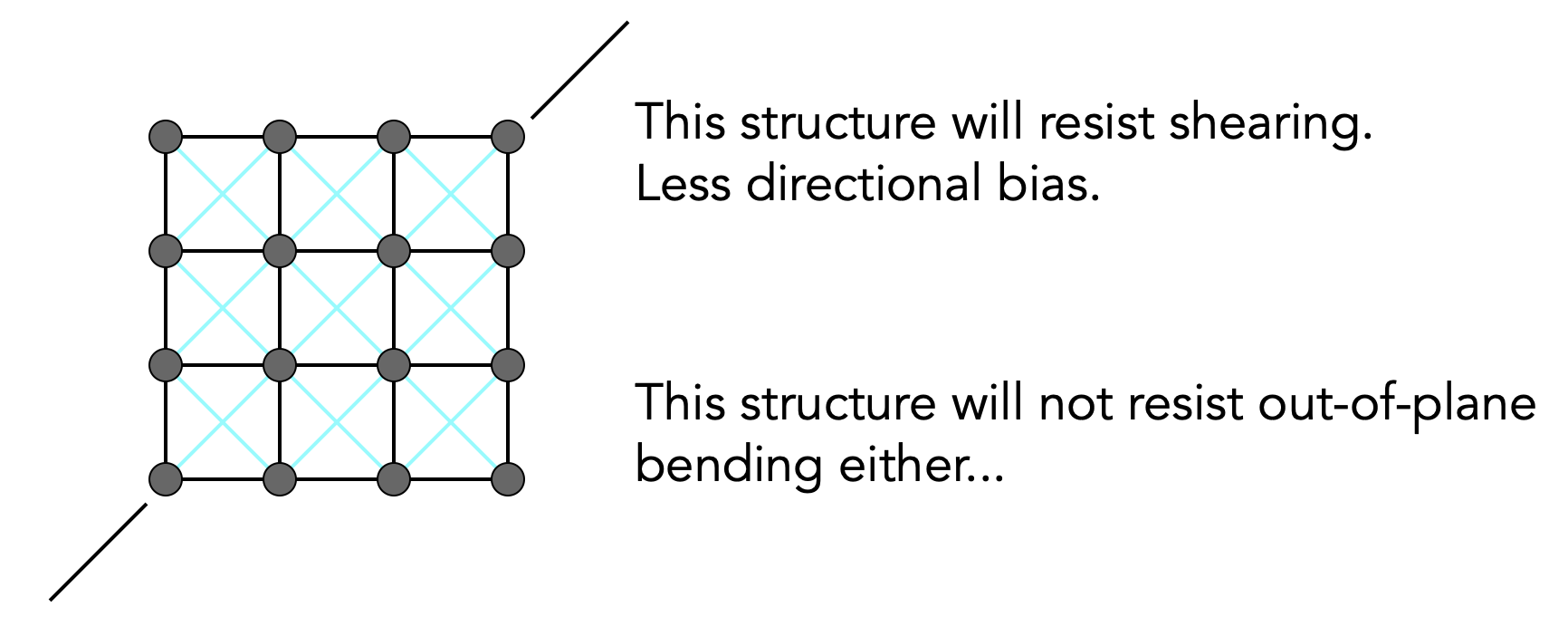
      • 解决：添加蓝色Spring，出现切变时，以提供对伉力；力较强截屏2023-06-23 15.10.06
    • Out-of-plane：布料因受力而形变至不在同一平面
      • 解决：添加Skip connection；力较弱，只起到辅助作用截屏2023-06-23 15.10.44
Aside: FEM (Finite Element Method) Instead of Springs
  • 考虑力的传导

Particle Systems

  • 本质：定义个体与群体的关系

  • 将动力学系统的模型定义为大量粒子的集合，每个粒子的运动都是由一组物理（或非物理）力来定义的

  • 挑战

    • 需要大量粒子（e.g. fluids
    • 需要考虑粒子间相互作用力（e.g. 碰撞、吸引力etc（实现困难
  • 对于每一帧动画
    • （if needed）生成新的粒子
    • 计算每一个粒子间作用力
    • 更新粒子的位置和速度
    • （if needed）根据粒子存活时间，remove the dead
    • 渲染
  • 粒子间的相互作用力
    • 截屏2023-06-23 15.29.29
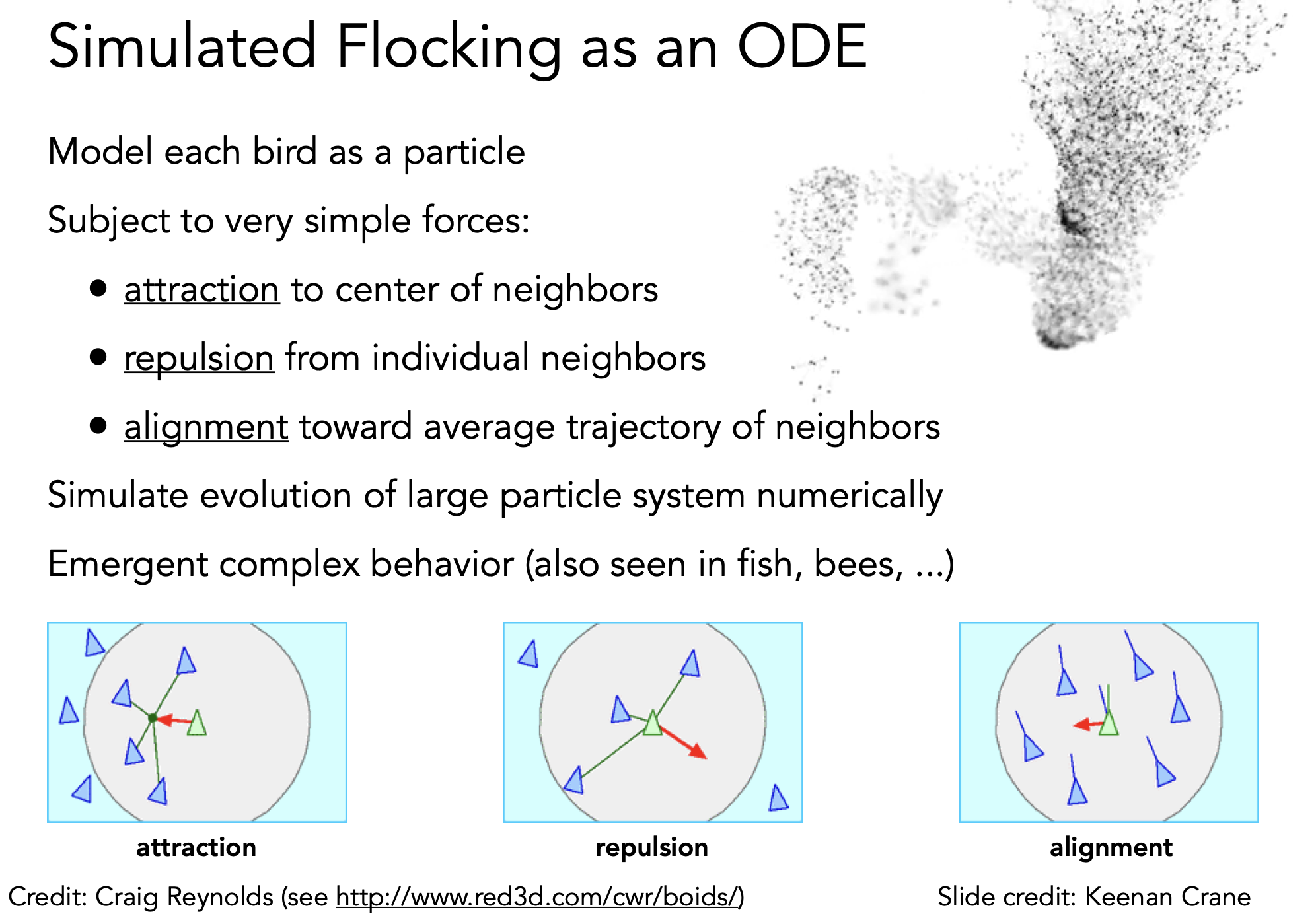
群体模拟
  • 鸟群
    • 截屏2023-06-23 15.34.44
  • 人群
    • 截屏2023-06-23 15.37.31

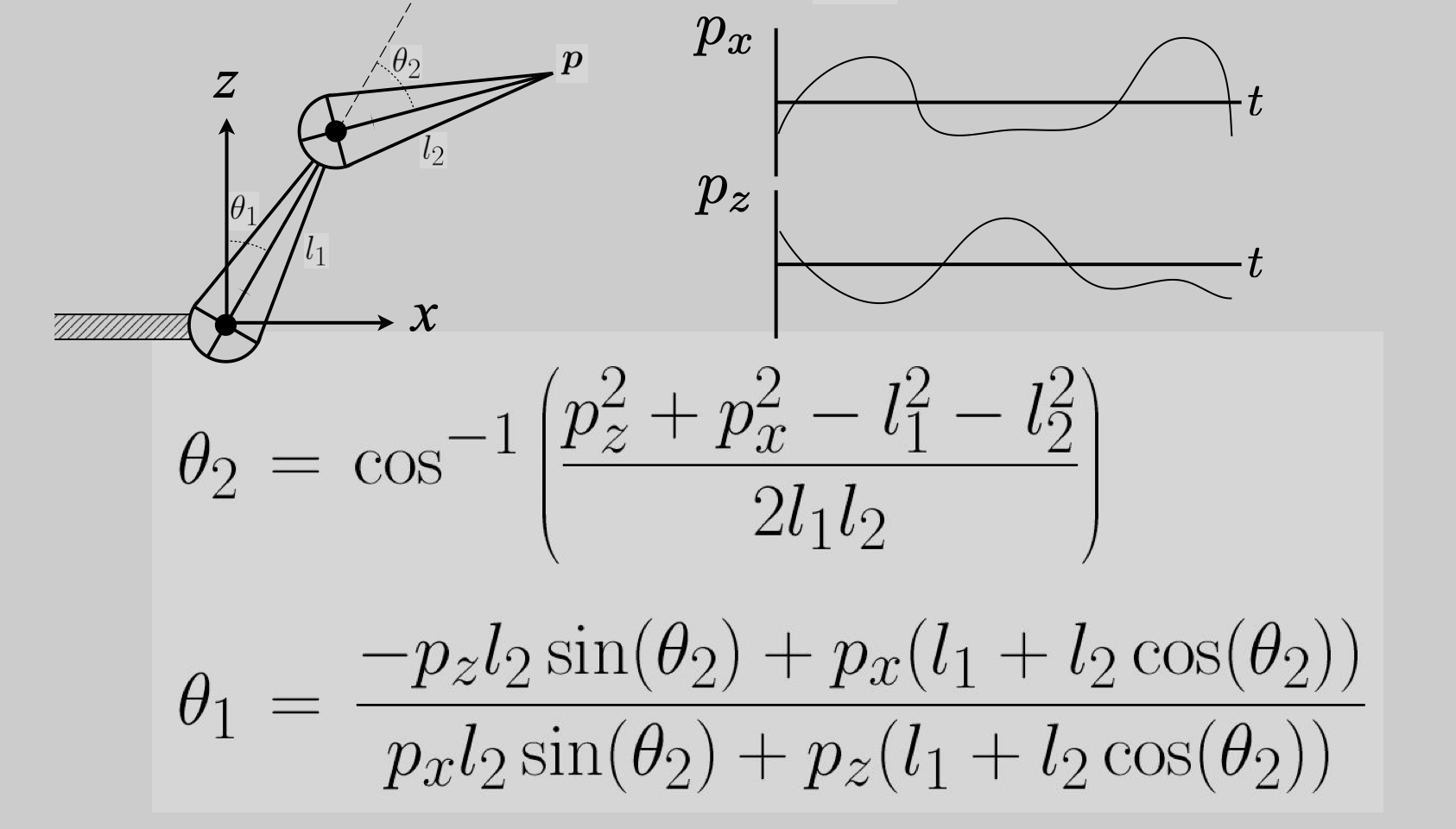
Kinematics 运动学

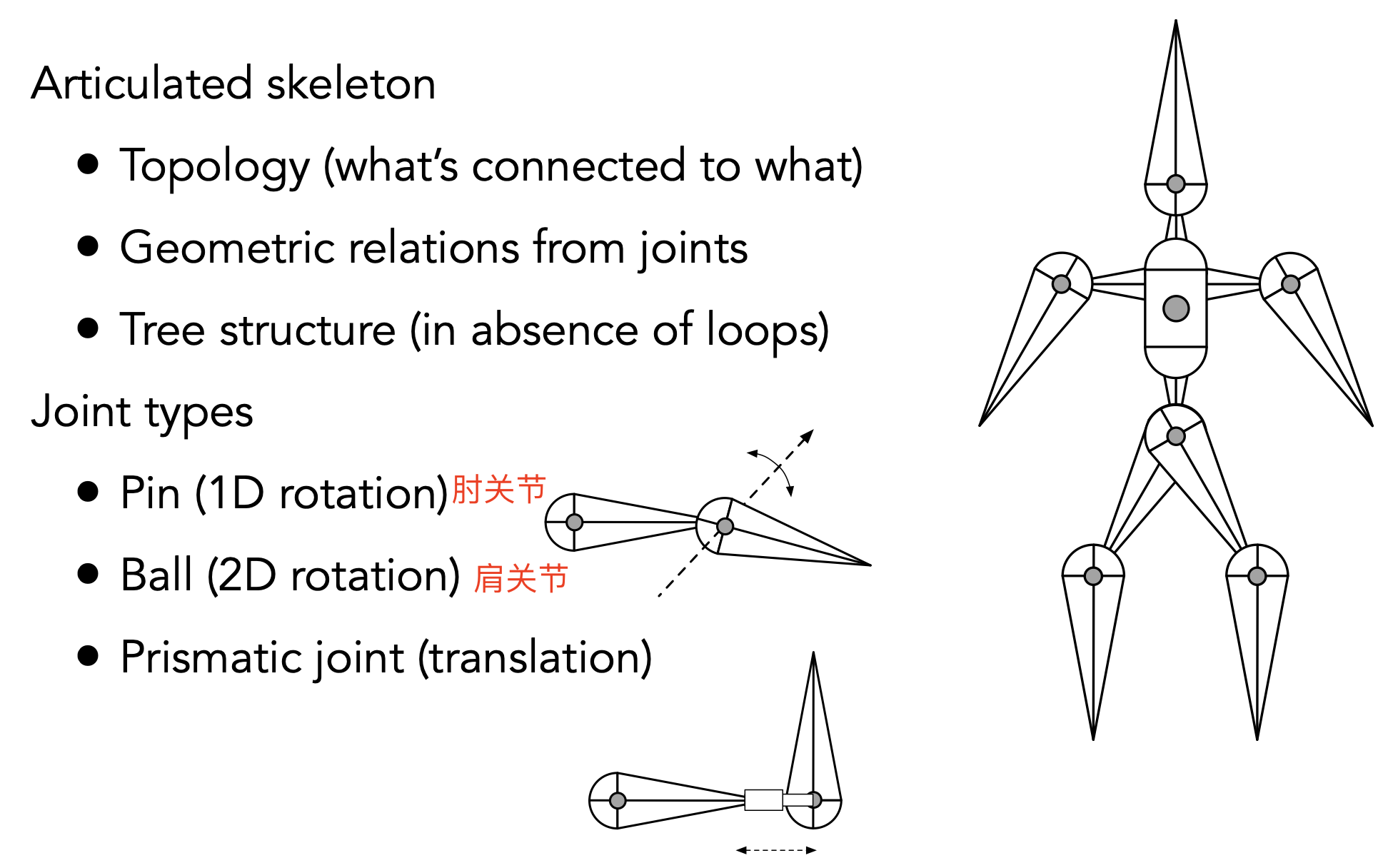
Forward Kinematics (FK)

  • 定义关节，形成骨骼结构
  • 关节分类
    • 截屏2023-06-23 15.39.56
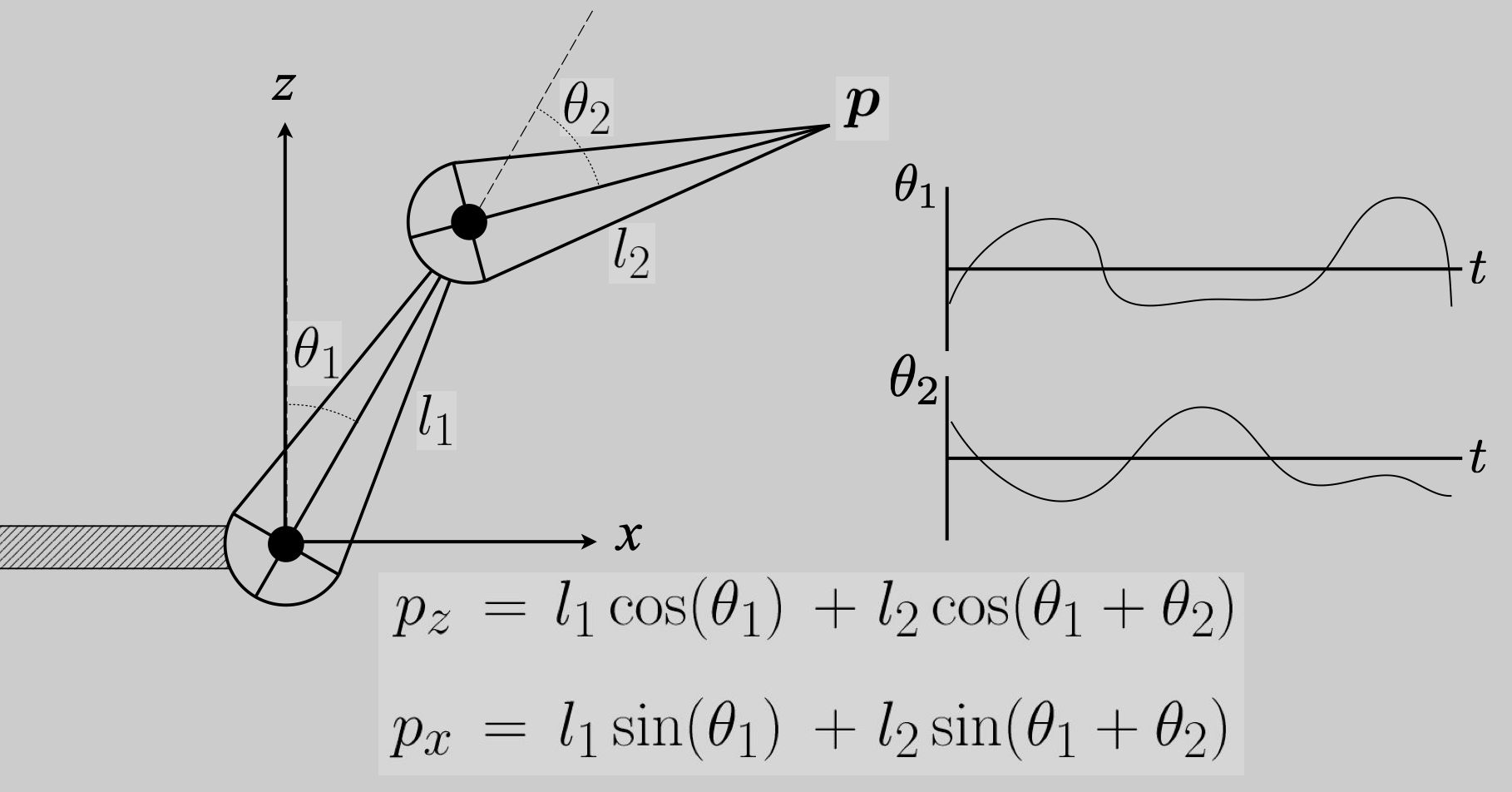
  • 计算：通过 $\theta_1 \& \theta_2$ 计算 $p$ 的位置
    • 截屏2023-06-23 15.43.53

Inverse Kinematics (IK)

  • 计算
    • 截屏2023-06-23 15.49.41
  • 问题：解不唯一
    • 解决方法：梯度下降截屏2023-06-23 16.01.46

Rigging

截屏2023-06-23 16.05.54

  • 对于形状的控制

  • Blend Shapes

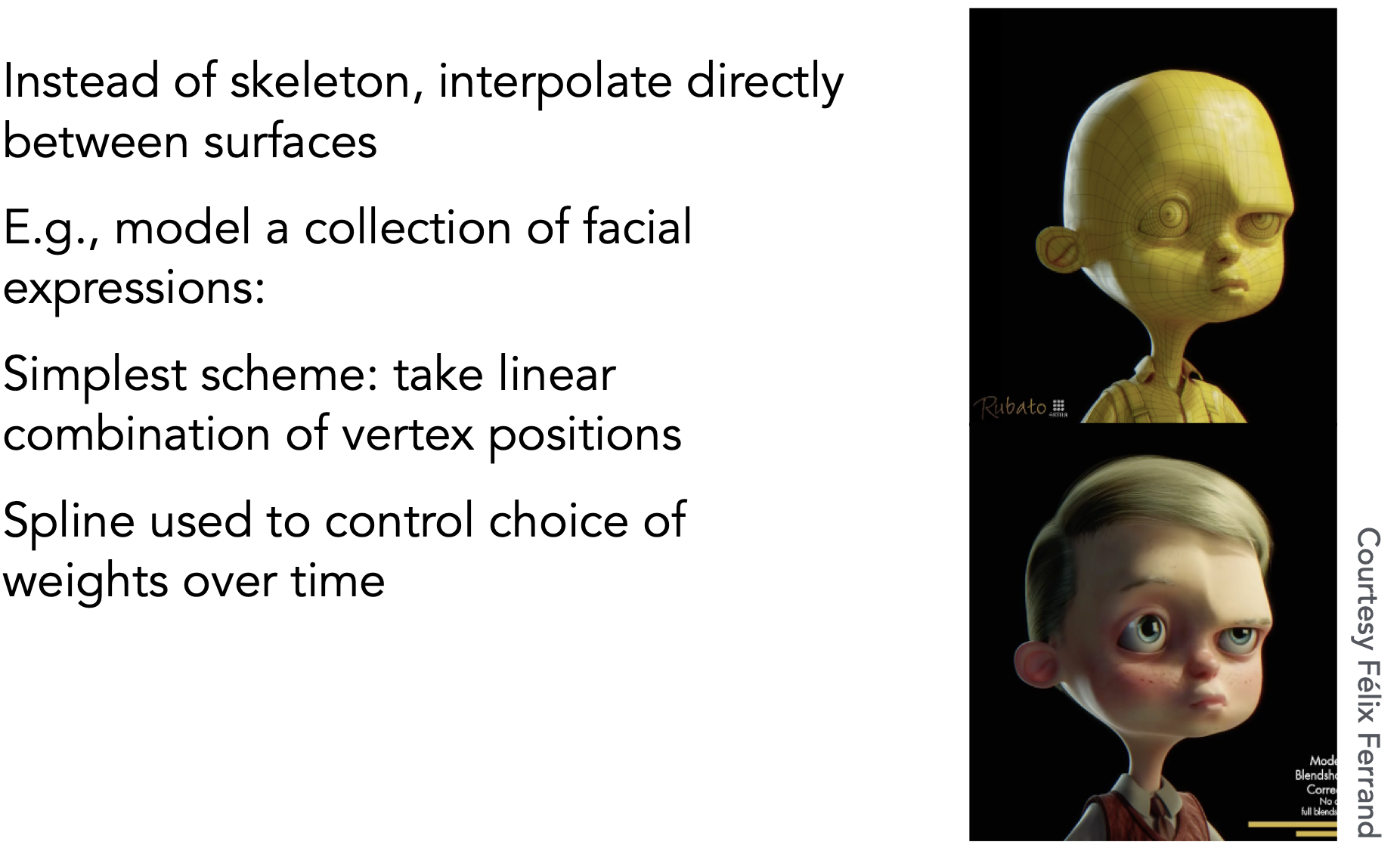
    • 两个不同的动作间，插值控制截屏2023-06-23 16.08.15

Motion Capture / Facial Motion Capture

截屏2023-06-23 16.19.10

截屏2023-06-23 16.20.44

截屏2023-06-23 16.21.38

P22

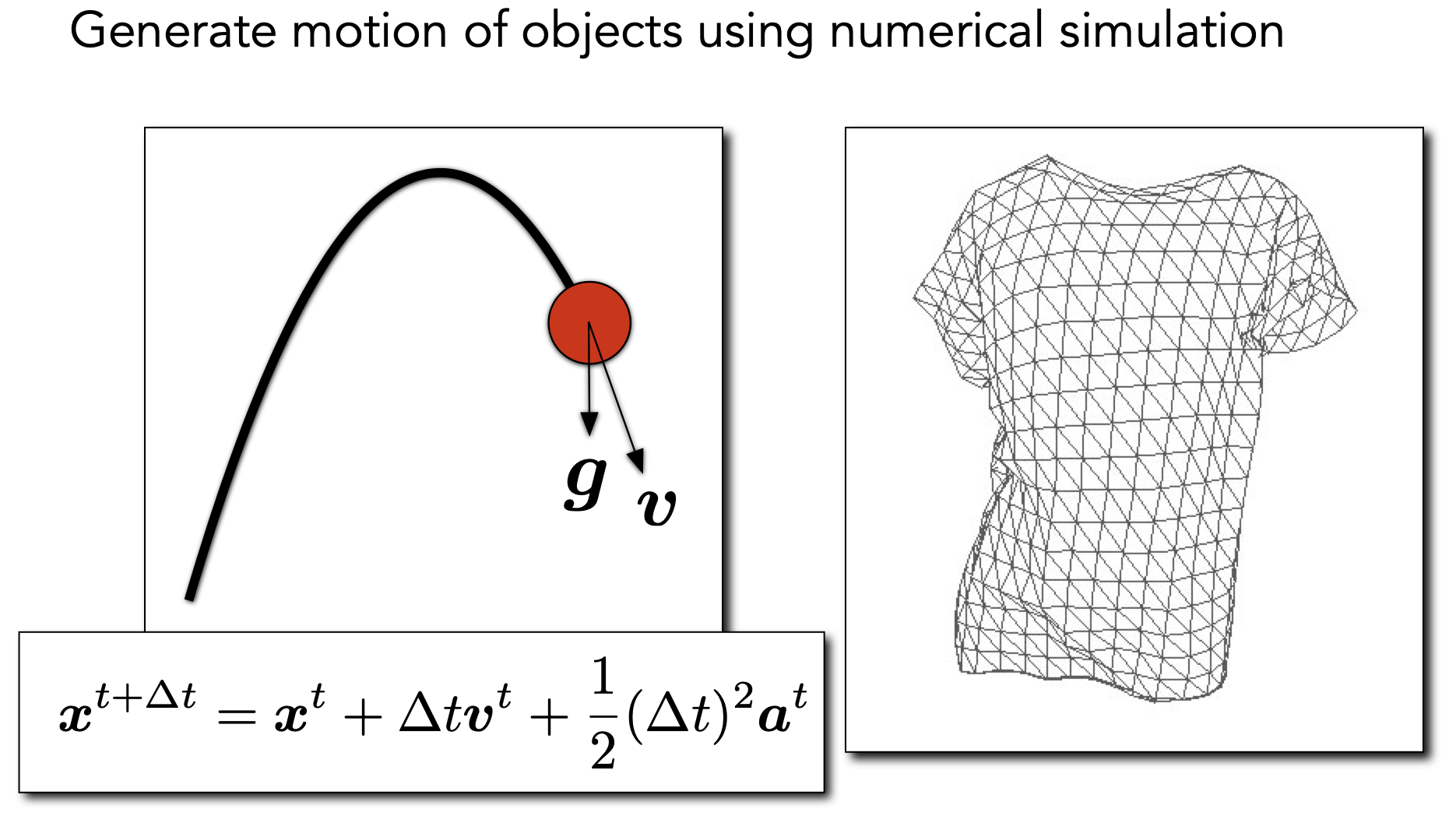
Single Particle Simulation

  • 已知初始位置和速度，解一段时间后的位置和速度

速度场

  • 速度场——理想情况

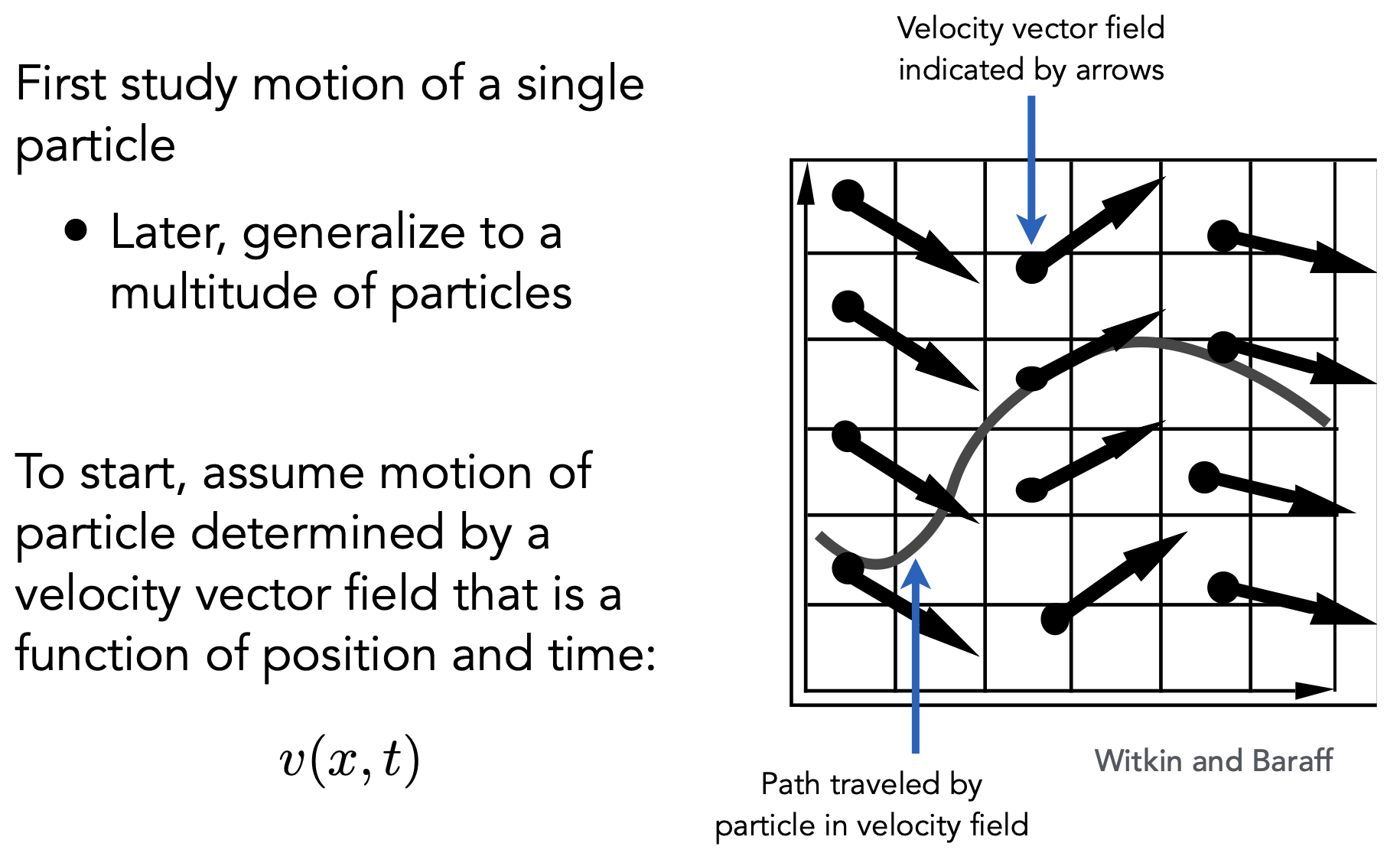
    • 给定位置$x$和时间$t$，都能知道速度；先考虑一个粒子，而后推广截屏2023-06-23 16.38.34

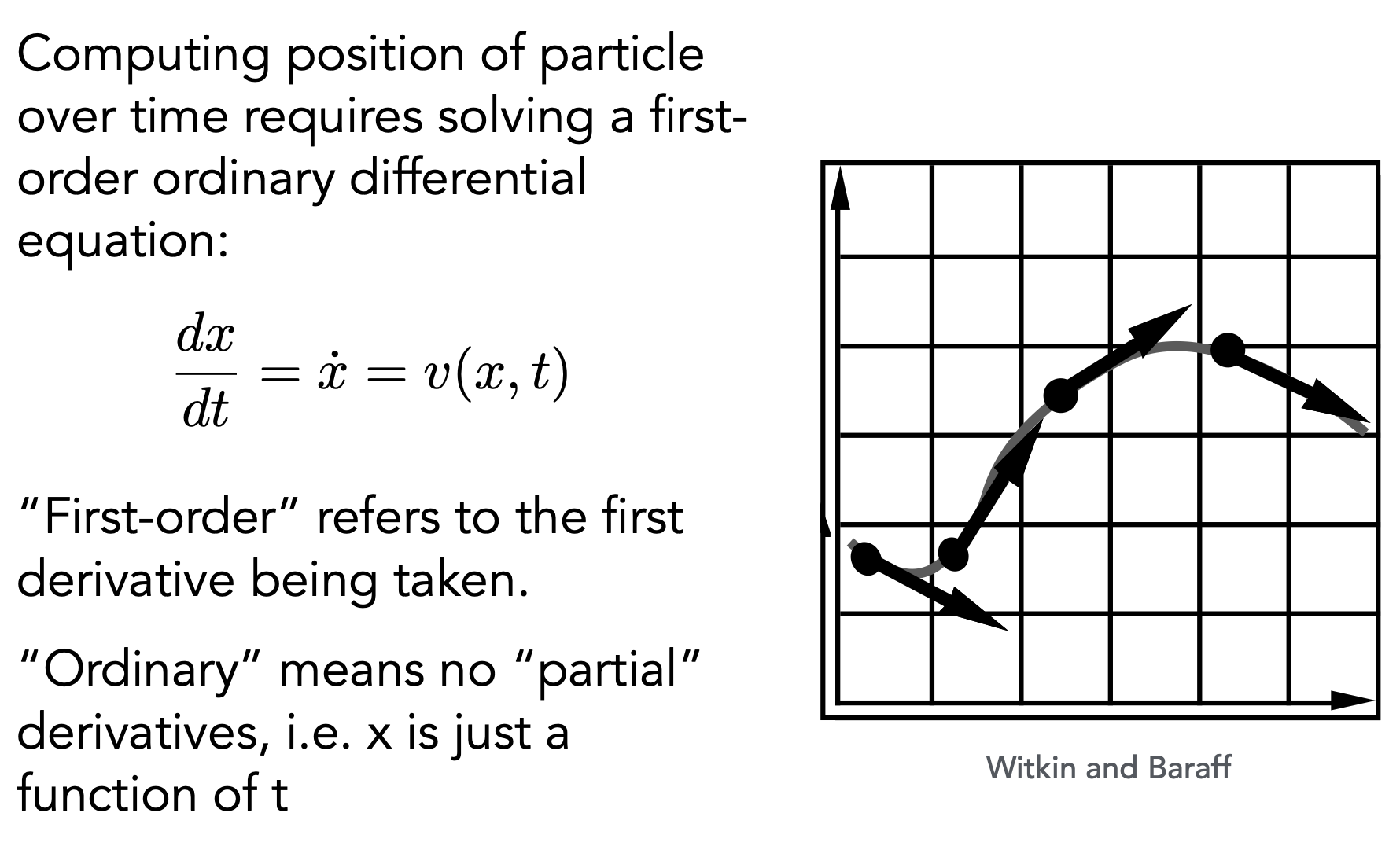
  • Ordinary Differential Equation (ODE) 常微分方程

    • 截屏2023-06-23 16.50.17
  • 需求：给定位置，求某一时刻的速度
  • 方法👇

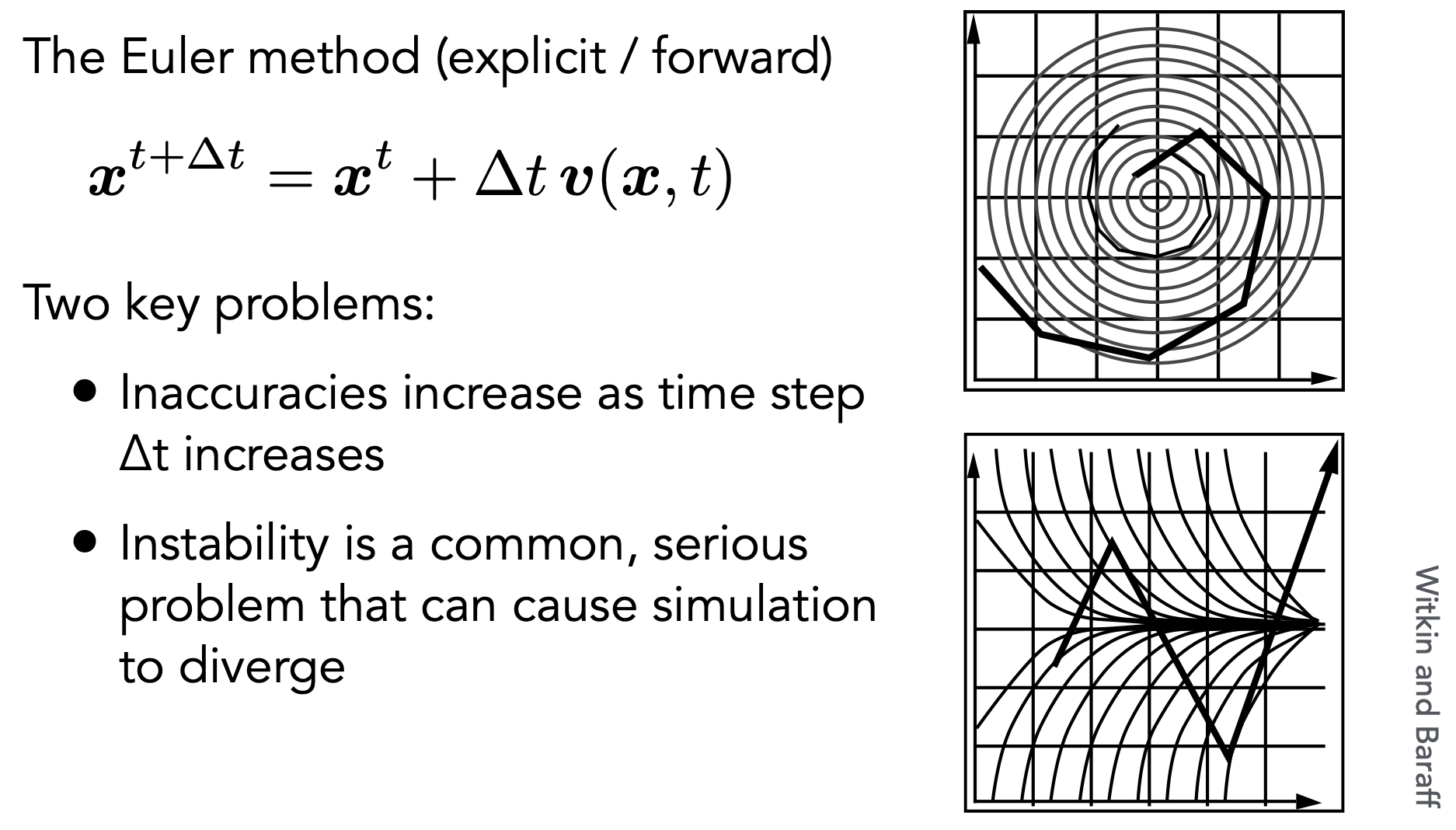
Euler’s Method 欧拉方法

截屏2023-06-23 16.54.22

  • 缺点
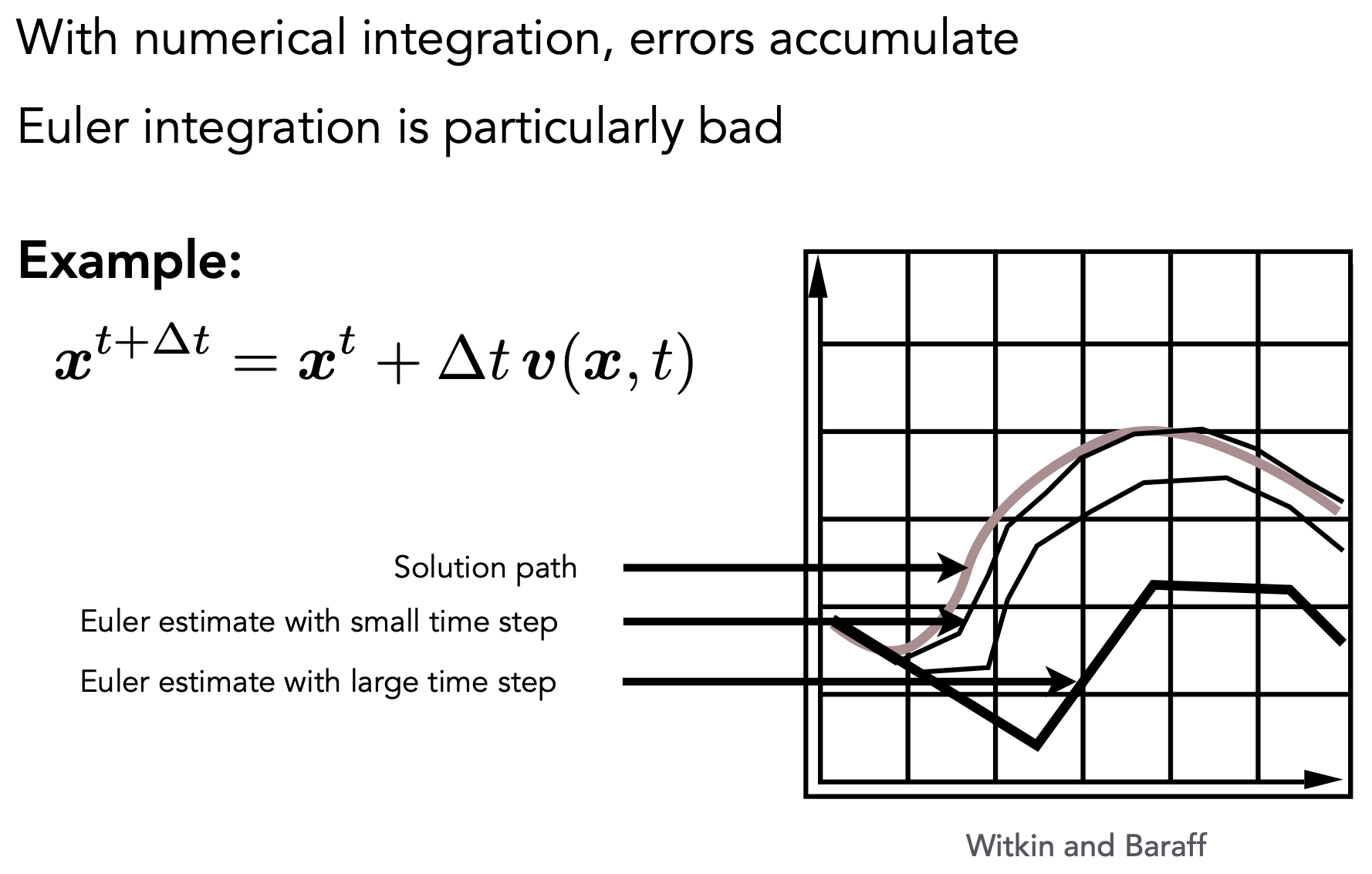
    • 误差。缩小步长可提高准确度截屏2023-06-23 16.58.37
    • 稳定性；出现正反馈，问题无限放大。如速度场为同心圆，理论上质点做圆周运动。但欧拉方法下无论步长多大，质点都会偏移圆周轨迹截屏2023-06-23 17.03.57

误差和稳定性

  • 误差
    • 每个时间步长上的误差都会累积。精度随着模拟的进行而降低
    • 准确性在图形学中可能并不重要

  • 稳定性

    • 错误可能会加剧，导致模拟发散(diverge)，即使底层系统没有
    • 缺乏稳定性是仿真中的一个基本问题，不容忽视

  • Combating Instability

    • Midpoint method：$\Delta t$ 时间，应运动到a。计算中点b的速度。对于起始点，应用中点b的速度，得到c
      • 截屏2023-06-23 17.21.26
    • Modified Euler：中点法展开式
      • $\Delta t^2$ 二次项，达到模拟抛物线的效果；泰勒展开
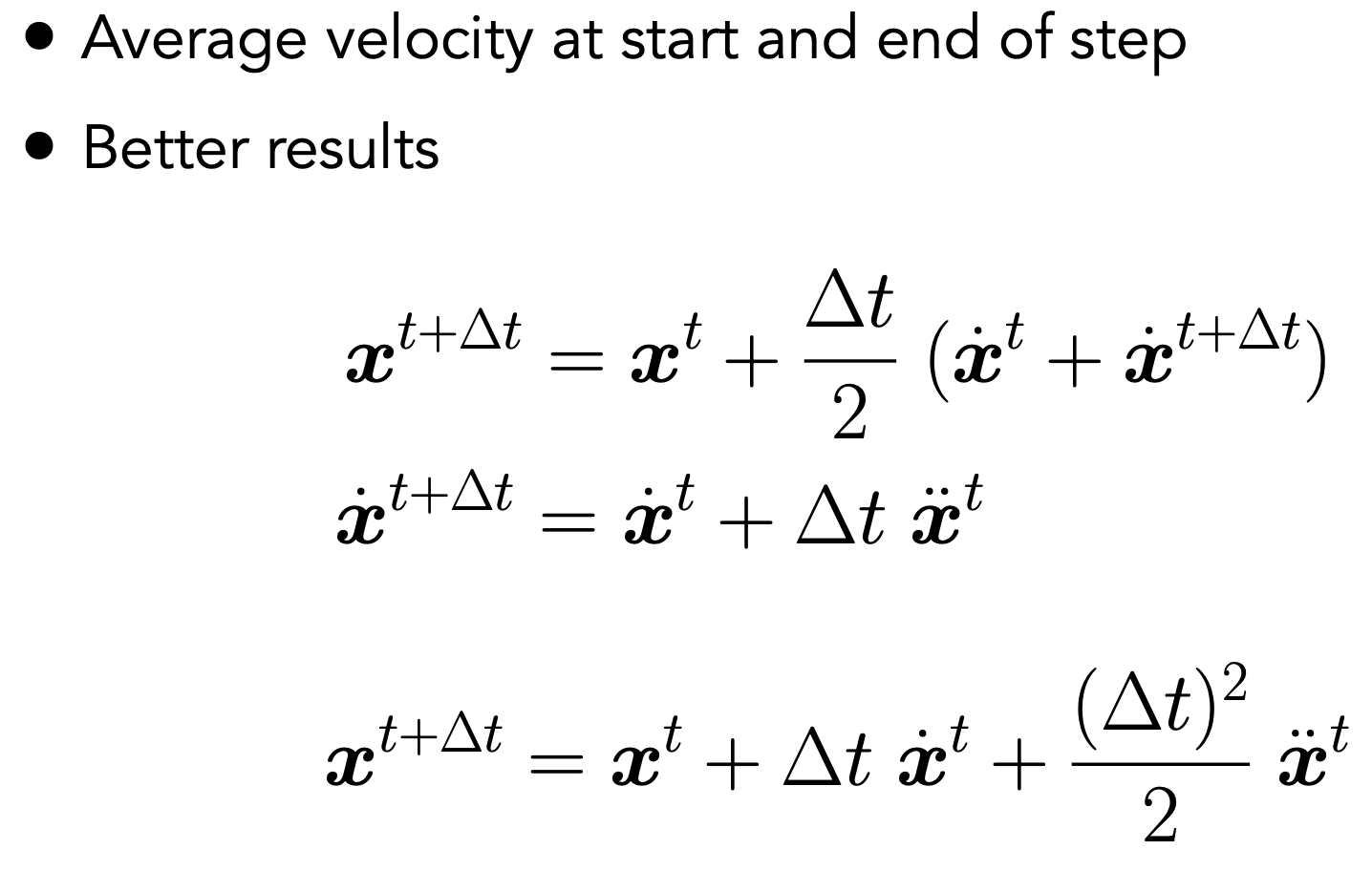
      • 截屏2023-06-23 17.28.51
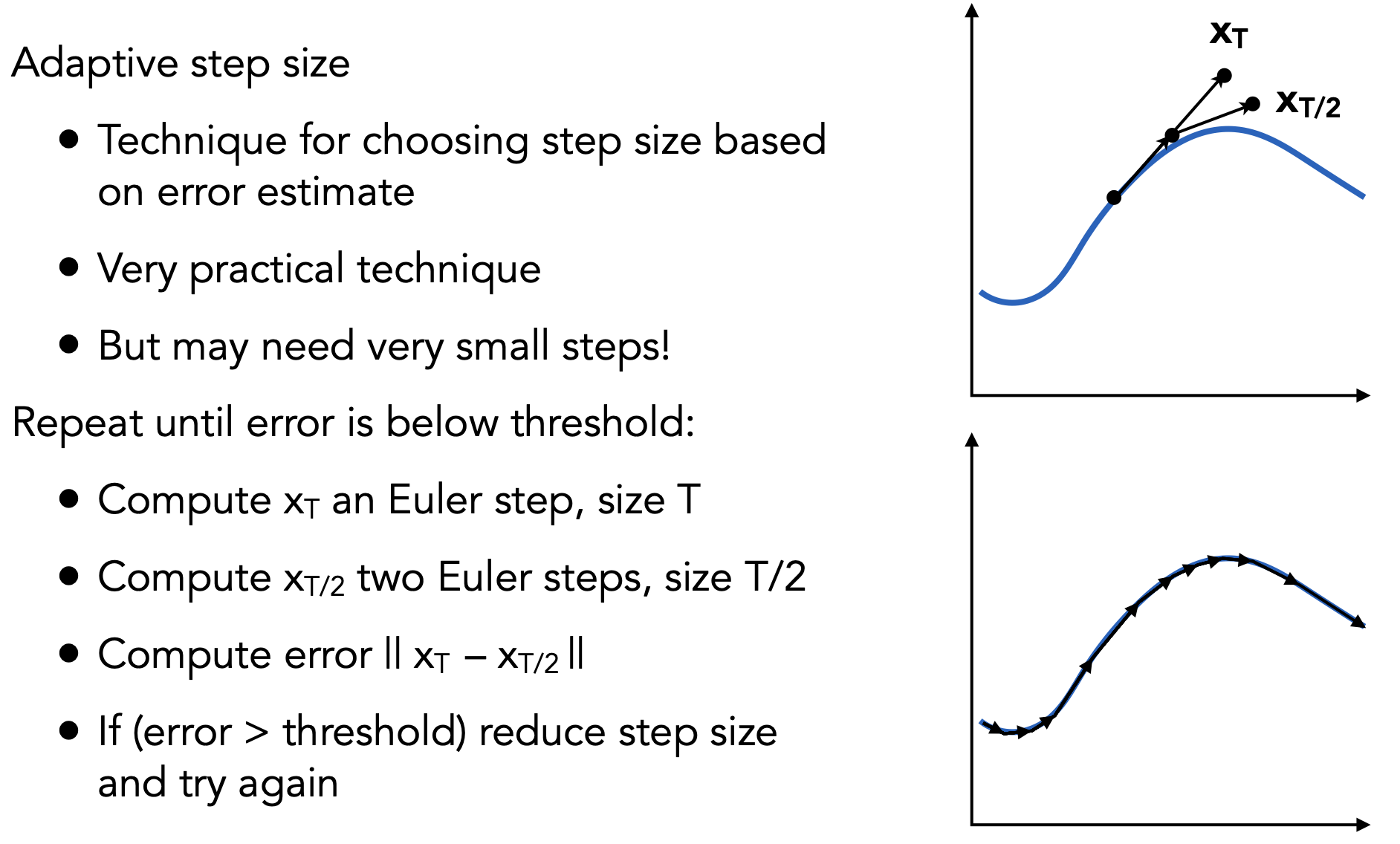
    • Adaptive step size：通过误差比较（$x_T$和$x_{T/2}$的差距），选择步长大小（是否还需继续二分）
      • 截屏2023-06-23 17.35.13
    • Implicit methods：使用下一个时间的速度和加速度进行求解
      • 截屏2023-06-23 17.42.58
      • 截屏2023-06-23 17.46.32
      • 补：龙哥库塔方法截屏2023-06-23 18.53.25
    • Position-based / Verlet integration：不基于物理
      • 截屏2023-06-23 18.58.37

Rigid Body Simulation 刚体模拟

截屏2023-06-23 19.01.27

  • 刚体：不发生形变
  • 刚体内部运动完全一致，因而刚体可看成一个粒子

Fluid Simulation

  • A Simple Position-Based Method
    • 通过模拟组成流体的小球的位置，模拟流体的运动
    • 截屏2023-06-23 19.06.11

Eulerian vs. Lagrangian

截屏2023-06-23 19.17.04

  • Material Point Method (MPM)
    • 截屏2023-06-23 19.20.55

OVER!

截屏2023-06-23 19.37.48