PBR补充笔记

引擎PBR公式基于微表面模型，BRDF：$f_r = f_{spec} + f_{diff}$

• 其中微表面BRDF高光部分：$f_{spec} = k_s \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}$，用于计算specular

  • $k_s$ 镜面反射比例

  • $\omega_o$ 为光线出射方向，即viewDir；$\omega_i$ 为光线入射方向，即lightDir

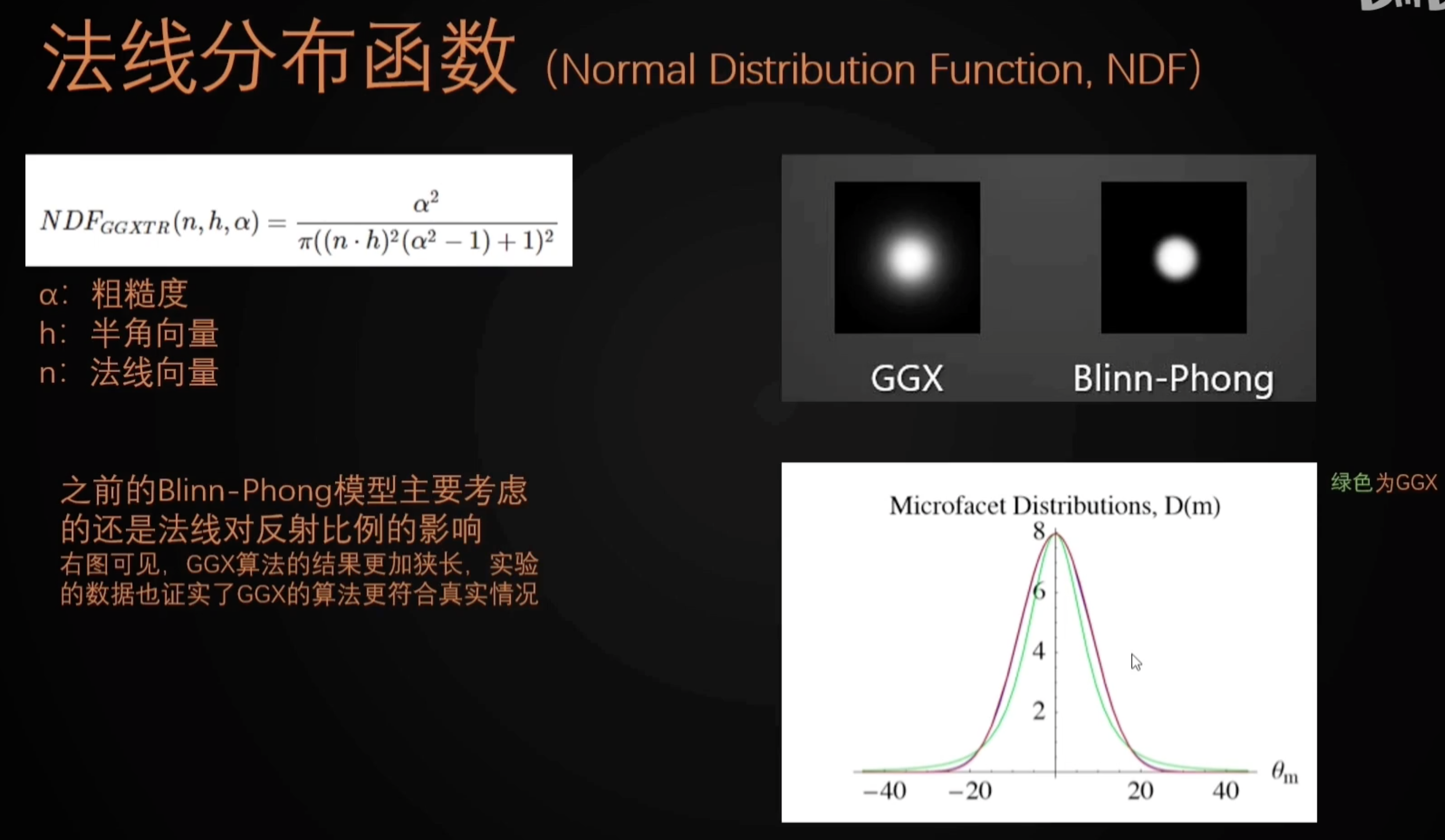
  • D为法线分布（描述漫反射/镜面反射）；$D = \frac{Roughness^2}{\pi (cos^2\theta_h(Roughness^2 -1 )+1)^2}$

  • F为菲涅尔项（描述反射、折射的能量分布）；$F = F_0 + (1-F_0)(1-cos\theta _h)^5$，$F_0$根据金属度发生变化

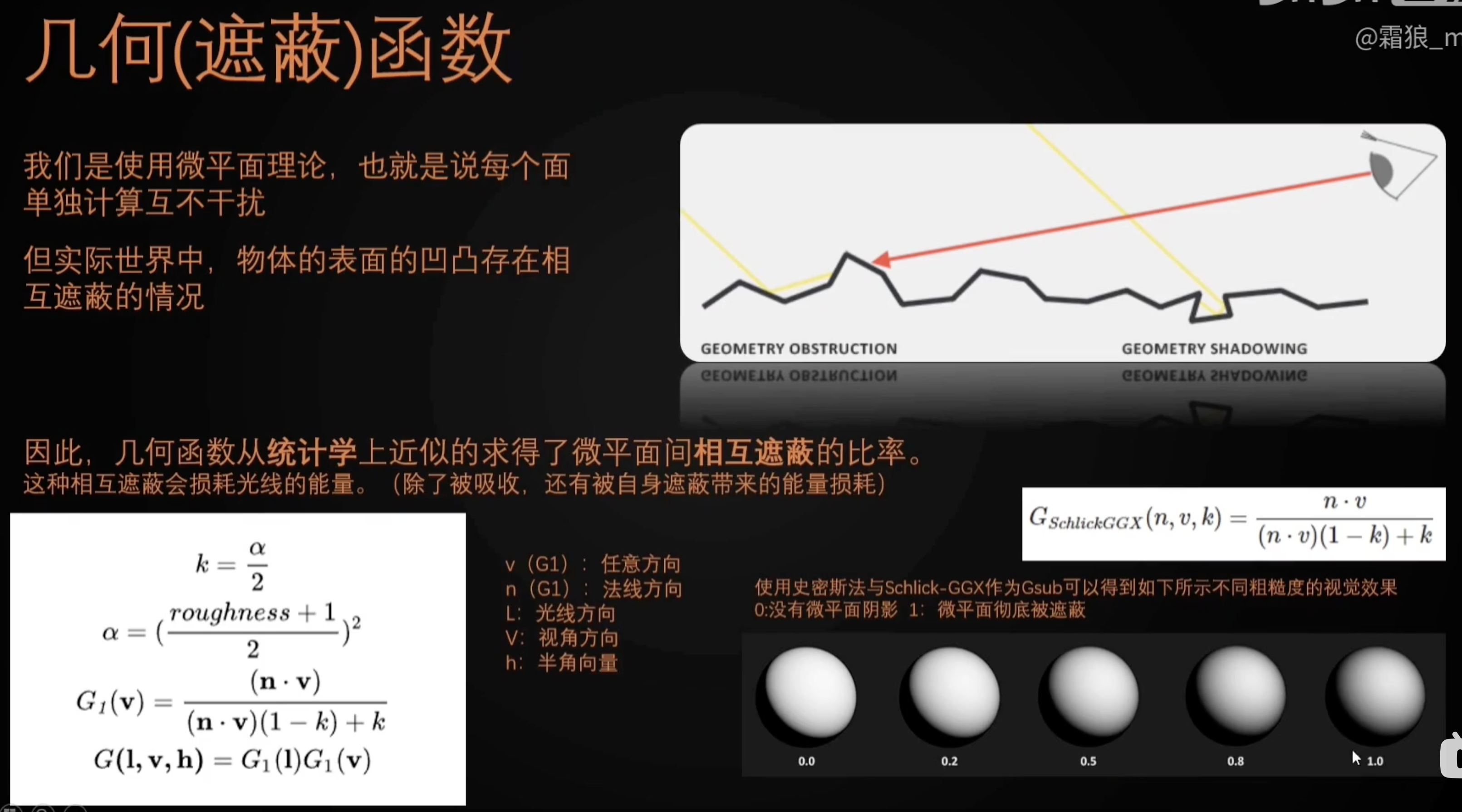
  • G为几何项（描述微表面间的相互遮挡）；$G = G_{GGX}(n\cdot l ,k) \cdot G_{GGX}(n\cdot v ,k)$，其中$G_{GGX}(float \quad dot ,float \quad k) = \frac{dot}{dot(1-k)+k}$，而$k = \frac{(Roughness + 1)^2}{8}$

• 其中微表面BRDF高光部分：$f_{diff} = k_d \frac{Diffuse}{\pi}$

  • $k_d$ 为漫反射比例

  • $Diffusion$ 为纹理颜色

• 将微表面BRDF带入反射方程：$L_0 = \int_\pi f_r \cdot L_i \cdot (\omega_i \cdot n)d\omega_i$

基于上述公式，可以实现引擎中PBR

PBR

• 基于物理

  • 基于材质
  • 基于光照
  • 基于相机

• 基于物理需满足

  • 微表面模型理论
  • 能量守恒

• 如何实现能量守恒

  • 
  • BRDF

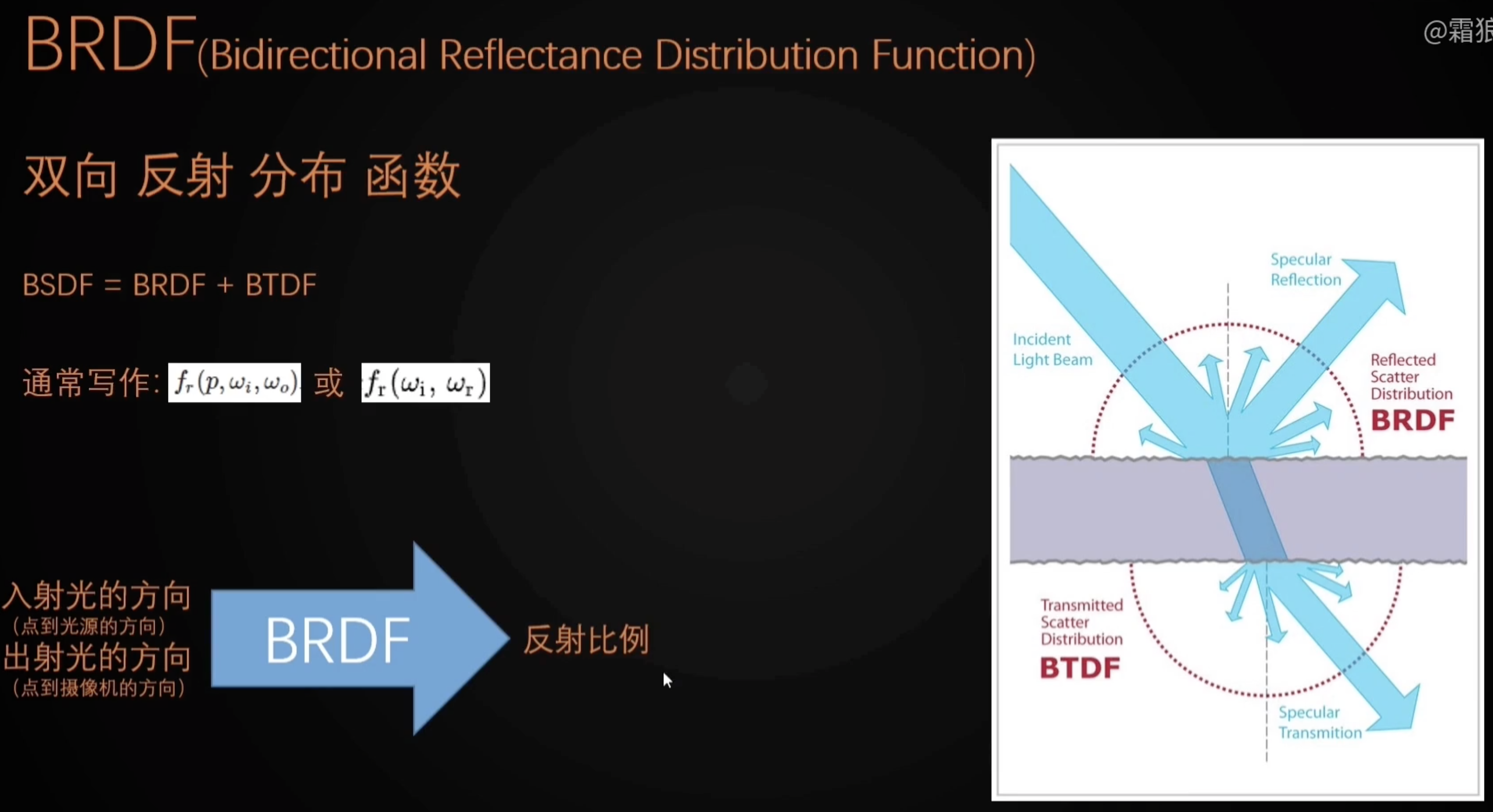
• Cook - Torrance反射率方程

  • 

• 高光部分

  • D：法线分布函数
    • GGX：更符合真实
      • 
  • G：几何遮蔽函数
    • 分为“几何遮蔽”和“几何阴影”
    • 
  • F：菲涅尔
    • 

Disney BRDF

• 使用直观的参数

• 参数尽可能少

• 参数在其合理范围内应为0～1

• 允许参数在有意义时超过这个范围

• 所有参数组合都应尽可能合理